Можно ли использовать дерево Штерна-Броко для лучшей сходимости $2^m/3^n$?
Обязательное чтение:
- Может ли любое положительное действительное число быть аппроксимировано как $2^m/3^n$ с участием $(m,n)$ достаточно большой?
- Последовательность дерева Броко Штерна
Причина, по которой я искал процедуру, у которой нет этого недостатка, т.е. где следующее приближение всегда ближе к желаемому результату. Это то, что я пробовал до сих пор.
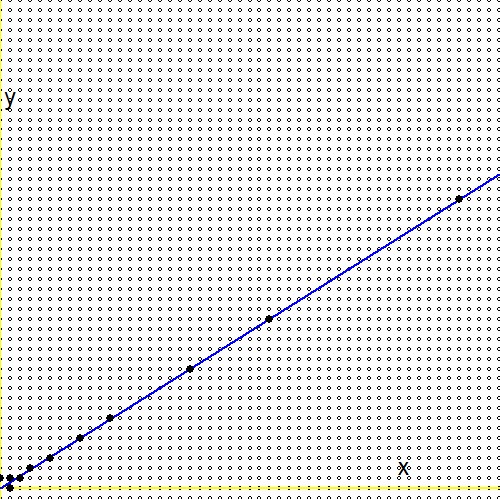
Согласно вопросу (2.) для каждого положительного действительного числа$0 \lt g \lt 1$, в дереве Стерна Броко [..] существует бесконечная последовательность, сходящаяся к действительному числу. Между тем, на этот вопрос есть ответ , и основной результат там звучит так: $$ - \frac{1}{n_1(n_1+n_2)} \lt g - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} $$ Принимая во внимание вопрос (1.), подставим $\ln(2)/\ln(3)$ для этого числа $g$. Из этого следует, что: $$ - \frac{1}{n_1(n_1+n_2)} \lt \frac{\ln(2)}{\ln(3)} - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} \\ - \frac{\ln(3)}{n_1} \lt \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \lt + \frac{\ln(3)}{n_2} \\ \ln\left(3^{-1/n_1}\right) \lt \ln\left(\frac{2^{n_1+n_2}}{3^{m_1+m_2}}\right) \lt \ln\left(3^{+1/n_2}\right) \\ 3^{-1/n_1} \lt \frac{2^{n_1+n_2}}{3^{m_1+m_2}} \lt 3^{+1/n_2} $$Можно изобразить поиск по дереву Штерна-Броко. Синяя линия - это функция $\,\color{blue}{x\ln(2)-y\ln(3)=0}\,$, маленькие кружки - дроби, нанесенные на сетку $\,m/n \to (m,n)\,$, массивные черные точки - это фракции в дереве Штерна-Броко. Видно, что поиск по дереву намного эффективнее увеличения $m$ а также $n$ с приращениями по одному.
Теперь сравните выражение во второй строке приведенных выше формул с аналогичным выражением в ссылке (1.): $$ \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \quad \Longleftrightarrow \quad m\ln(2) - n\ln(3) - \ln(r) $$ И будьте готовы к разочарованию: логарифм произвольного действительного $r$пропал, отсутствует! Или альтернативно:$\ln(r)=0$ или же $r=1$. Это означает, что наш «бесконечный поиск» по дереву Штерна-Броко, хотя и очень эффективен, в конечном итоге приводит к приближению только для числа один. Я нахожу это странным, потому что - графически - не кажется большой разницы между$\color{red}{2^m/3^n \to r}$ а также $\color{blue}{2^m/3^n \to 1}$:
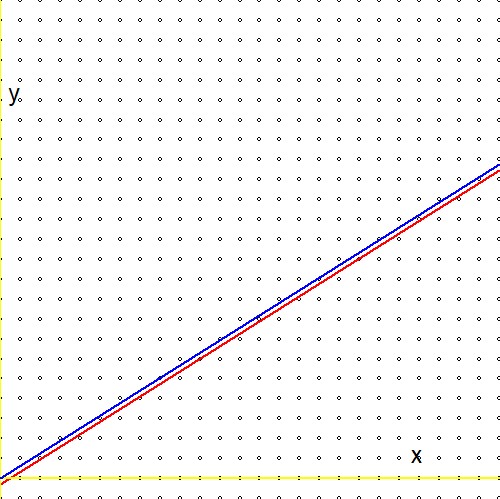
Отсюда ВОПРОС: существует ли средство для адаптации процедуры Штерна-Брокота, чтобы она работала для других вещественных чисел, кроме одного?
РЕДАКТИРОВАТЬ.
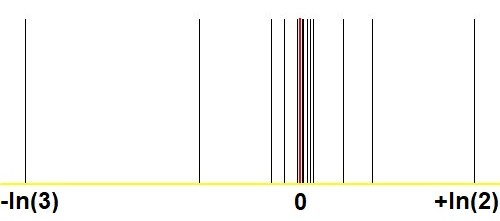
А вот еще один график , который показывает удивительное сближение с методом Штерна-Броко, по сравнению с аналогичными фотографии в моем Q & A может любой положительной вещественной быть аппроксимирована$2^m/3^n$ с участием $(m,n)$достаточно большой? :
Ответы
Я дам подход, в котором не используется процедура Штерна-Брокота.
Достаточно показать, что $\frac{2^{m}}{3^{n}}$плотно в интервале [1,2]. С принятием$\alpha\in (0,\infty)$ вне этого интервала есть некоторые $k\in Z$ чтобы $\alpha = 2^{k}\gamma $ для некоторых $\gamma \in [1,2]$. Тогда мы знаем, что есть последовательность в$\frac{2^{m}}{3^{n}}$ который приближается $\gamma$, почленно умножая последовательность на $2^{k}$ (возможно, взяв хвост последовательности), мы получаем последовательность в $\frac{2^{m}}{3^{n}}$ который приближается $\alpha$.
Затем учтите, что карта $f:[1,2] -> [0,1]$ с участием $f(x) = log_{2}(x)$ это биекция.
Образ $\frac{2^{m}}{3^{n}}$ под картой $N-Nlog_{2}(3)$. Так что достаточно показать, что$N-Nlog_{2}(3)$ плотно в $[0,1]$.
Это следствие теоремы Вейля о равнораспределении, которая является частным случаем эргодической теоремы.
Рассмотреть возможность $a=2-log_{2}(3) = log_{2}(\frac{4}{3})$, так $a$ есть в образе набора, так это $na = log_{2}(\frac{4^{n}}{3^{n}})$ и дробная часть $na$.
Теорема Вейля о равнораспределении (которая не является тривиальным результатом) показывает, что для иррационального a дробная часть $na$равномерно распределен и, следовательно, плотен на [0,1]. С$2-log_{2}(3)$ иррационально, вы можете использовать эту теорему.