¿Se puede emplear el árbol de Stern-Brocot para una mejor convergencia de $2^m/3^n$?
Lectura previa:
- ¿Se puede aproximar cualquier real positivo como$2^m/3^n$con$(m,n)$¿lo suficientemente grande?
- Secuencia del árbol Stern Brocot
Razón por la cual he estado buscando un procedimiento que no tenga este inconveniente, es decir, donde la siguiente aproximación sea siempre más cercana al resultado deseado. Esto es lo que he intentado hasta ahora.
Según la pregunta (2.), para todo número real positivo$0 \lt g \lt 1$, existe una sucesión infinita en el árbol de Stern Brocot [ .. ] que converge al número real. Mientras tanto, esta pregunta tiene una respuesta , y el resultado principal allí dice lo siguiente: $$ - \frac{1}{n_1(n_1+n_2)} \lt g - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} $$En vista de la pregunta (1.), sustituimos $\ln(2)/\ln(3)$por ese numero $g$. Entonces se sigue que: $$ - \frac{1}{n_1(n_1+n_2)} \lt \frac{\ln(2)}{\ln(3)} - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} \\ - \frac{\ln(3)}{n_1} \lt \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \lt + \frac{\ln(3)}{n_2} \\ \ln\left(3^{-1/n_1}\right) \lt \ln\left(\frac{2^{n_1+n_2}}{3^{m_1+m_2}}\right) \lt \ln\left(3^{+1/n_2}\right) \\ 3^{-1/n_1} \lt \frac{2^{n_1+n_2}}{3^{m_1+m_2}} \lt 3^{+1/n_2} $$Se puede representar la búsqueda a través del árbol Stern-Brocot. La línea azul es la función. $\,\color{blue}{x\ln(2)-y\ln(3)=0}\,$, los círculos pequeños son fracciones, representados en una cuadrícula $\,m/n \to (m,n)\,$, puntos masivamente rellenos de negro son las fracciones en el árbol de Stern-Brocot. Se ve que buscar a través del árbol es mucho más eficiente que aumentar $m$y $n$con incrementos uno a la vez.
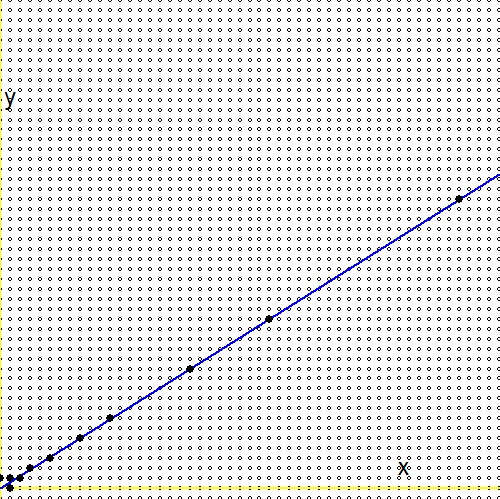
Ahora compare la expresión en la segunda línea de las fórmulas anteriores con una expresión análoga en la referencia (1.):$$ \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \quad \Longleftrightarrow \quad m\ln(2) - n\ln(3) - \ln(r) $$Y prepárate para una decepción: el logaritmo del real arbitrario$r$¡Está perdido! O alternativamente:$\ln(r)=0$o$r=1$. Esto significa que nuestra "búsqueda infinita" a través del árbol de Stern-Brocot, aunque muy eficiente, finalmente llega a una aproximación solo para el número uno. Encuentro esto extraño, porque - gráficamente - no parece haber una gran diferencia entre$\color{red}{2^m/3^n \to r}$y$\color{blue}{2^m/3^n \to 1}$:
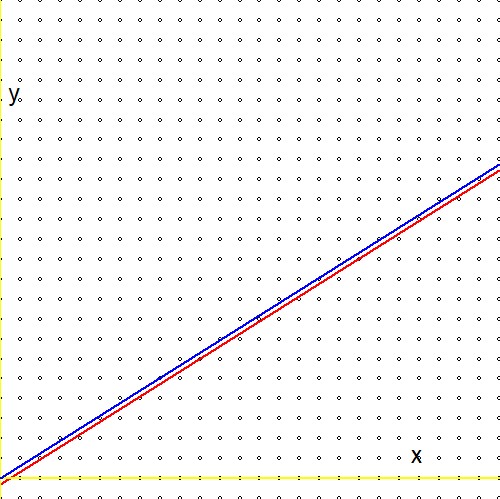
De ahí la PREGUNTA: ¿existe un medio para adaptar el procedimiento de Stern-Brocot de modo que funcione para otros reales distintos de uno?
EDITAR.
Aquí viene otro gráfico que muestra la asombrosa convergencia con el método de Stern-Brocot, en comparación con imágenes análogas en mis preguntas y respuestas. ¿Se puede aproximar cualquier real positivo como$2^m/3^n$con$(m,n)$¿lo suficientemente grande? :
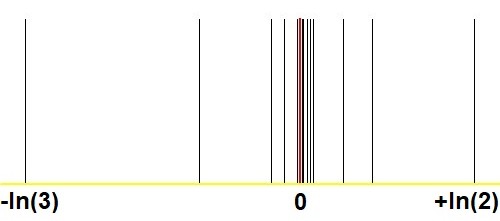
Respuestas
Daré un enfoque que no utiliza el procedimiento de Stern-Brocot.
Basta con demostrar que$\frac{2^{m}}{3^{n}}$es denso en el intervalo [1,2]. Desde que tomo$\alpha\in (0,\infty)$fuera de este intervalo hay algunos$k\in Z$así que eso$\alpha = 2^{k}\gamma $para algunos$\gamma \in [1,2]$. Entonces sabemos que hay una secuencia en$\frac{2^{m}}{3^{n}}$que se acerca$\gamma$, multiplicando la sucesión en términos de$2^{k}$(posiblemente tomando una cola de la secuencia), obtenemos una secuencia en$\frac{2^{m}}{3^{n}}$que se acerca$\alpha$.
Luego considere que el mapa$f:[1,2] -> [0,1]$con$f(x) = log_{2}(x)$es una biyección.
La imagen de$\frac{2^{m}}{3^{n}}$debajo del mapa esta$N-Nlog_{2}(3)$. Entonces es suficiente demostrar que$N-Nlog_{2}(3)$es denso en$[0,1]$.
Esta es una consecuencia del teorema de equidistribución de Weyl, que es un caso especial del teorema ergódico.
Considerar$a=2-log_{2}(3) = log_{2}(\frac{4}{3})$, entonces$a$está en la imagen del conjunto, así es$na = log_{2}(\frac{4^{n}}{3^{n}})$y también lo es la parte fraccionaria de$na$.
El teorema de equidistribución de Weyl (que no es un resultado trivial) muestra que para a irracional la parte fraccionaria de$na$se distribuye uniformemente y, por lo tanto, es denso en [0,1]. Ya que$2-log_{2}(3)$es irracional puedes usar este teorema.