¿Qué tan grande debería ser un código QR en mi techo para que un satélite pueda escanearlo dada la resolución permitida de hoy?
Digamos, usando los satélites Planet Labs
Gracias
Respuestas
¿Qué tan grande debería ser un código QR en mi techo para que un satélite pueda escanearlo dada la resolución permitida de hoy?
Digamos, usando los satélites Planet Labs
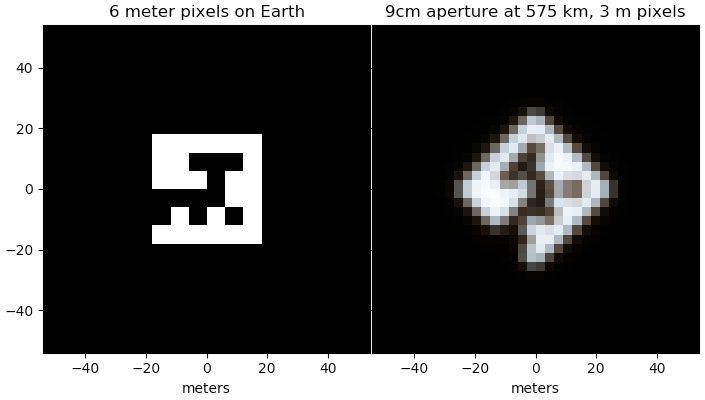
Esta es una respuesta complementaria. He simulado píxeles "QR" de 6 metros como se ve desde el espacio con una apertura de 9 cm (en el extremo de un cubo Dove de 3U) en longitudes de onda de 450, 550 y 650 nm, rotados a 45 grados y luego muestreados con píxeles de 3 metros.
Es un guión rudimentario y frágil, pero funciona.
La imagen apoya la conclusión principal en la otra respuesta de que este es probablemente el tamaño mínimo para cierta confiabilidad de verlo con una paloma.
El guión es subóptimo, era vago y usé PIL para rotar, podría haber interpolado scipy.ndimage.map_coordinatesy podría haber "fuzzificado" en scipy.ndimage.gaussian_filterlugar de un elegante disco Airy.
Los matices en la imagen final se deben a los límites de difracción de la apertura dependientes de la longitud de onda, aproximadamente $1.22 \lambda / D$ variación de la resolución angular con la relación entre la longitud de onda y la apertura.
import numpy as np
import matplotlib.pyplot as plt
import itertools
from PIL import Image
from scipy import special as spe
from scipy.ndimage import convolve
N = 5*2
data = ('111111' + '110001' + '111011' +
'000011' + '010101' + '111111')
data = np.array([int(x) for x in data]).reshape((6, 6))
data = np.pad(data, ((6, 6), (6, 6)))
img = np.zeros((N*18, N*18, 3))
for i, j in itertools.product(np.arange(18), repeat=2):
img[N*i:N*(i+1), N*j:N*(j+1)] = data[i, j]
pixsize = 6 # meters
scale = pixsize/N
extent = 9*N * scale * np.array([-1, 1, -1, 1])
R = 575 * 1000. # meters distance
x = 4*N * scale * np.linspace(-1, 1, 8*N)
X, Y = np.meshgrid(x, x)
q = np.sqrt(X**2 + Y**2)
wavelengths = 1E-09 * np.array([650, 550, 450])
a = 0.045 # radius of aperture in meters (looking out end of a 3U cubesat)
x = (2 * np.pi * a / wavelengths) * (q[..., None] / R)
# https://en.wikipedia.org/wiki/Airy_disk
airy = (2 * spe.j1(x) / x)**2
areas = airy.sum(axis=0).sum(axis=0)
airy /= areas
new = [convolve(img[..., i], airy[..., i]) for i in range(3)]
newarray = np.stack(new, axis=2)
newarray = np.uint8(255 * newarray/newarray.max())
newimg = Image.fromarray(newarray)
newimg45 = newimg.rotate(45)
newimg45.show()
n45 = np.array(list(newimg45.getdata())).reshape(18*2, N>>1, 18*2, N>>1, 3)
n45 = np.uint8(n45.sum(axis=(1, 3)) / (N>>1)**2)
if True:
plt.figure()
plt.subplot(1, 2, 1)
plt.imshow(img, extent=extent)
plt.title('6 meter pixels on Earth')
plt.xlabel('meters')
plt.subplot(1, 2, 2)
plt.imshow(n45, extent=extent)
plt.title('9cm aperture at 575 km, 3 m pixels')
plt.xlabel('meters')
plt.show()
¿Qué tan grande debería ser un código QR en mi techo para que un satélite pueda escanearlo dada la resolución permitida de hoy?
Digamos, usando los satélites Planet Labs
tl; dr: usando 6x6 " etiqueta de realidad aumentada " discutida en la respuesta de @ CamilleGoudeseune como la del rover Curiosity y píxeles de 6 metros (el doble de resolución mínima para permitir una traducción y rotación arbitrarias) su patrón debe ser de 36 x 36 metros para tener un buen cambio de ser visto y recuperado de una imagen de una paloma de PlanetLabs.
Quitaría la reflectividad roja e infrarroja de las áreas brillantes y codificaría solo en las longitudes de onda más cortas, ya que las Doves tienen cuatro canales de color que (probablemente) están limitados por difracción y las longitudes de onda más largas pueden tener una peor resolución.
Intente excitar solo las bandas de longitud de onda más cortas de su nave espacial objetivo para hacerlas "emergentes" para los espectadores casuales, o solo mire esas longitudes de onda en el producto de datos final si lo está buscando usted mismo.
A https://www.planet.com/products/planet-imagery/los satélites o "palomas" más numerosos proporcionan datos para el producto de datos PLANETSCOPE. Se dice que los satélites tienen una resolución de 3,7 metros y el producto de datos tiene un tamaño de píxel muestreado de 3 metros. Consulte también la respuesta de @ djr a ¿Son estas imágenes de Planet Labs? ¿Están las imágenes a disposición del público?
Si tuvieras mucha suerte de tener los píxeles alineados con tu patrón QR tanto de traslación como de rotación, teóricamente podrían ser de 3 metros.
Sin embargo, en la práctica, dada la traducción y rotación arbitrarias de su patrón dentro del campo de la imagen, debería tener un factor de al menos 2, si no 3, más grande que esto.
@Uwe nos recuerda que un código QR pequeño aún sería bastante grande. Hay códigos Micro QR de 11 x 11 y la gente del espacio ha utilizado números de píxeles aún más pequeños para alternativas a los códigos QR con incluso menos píxeles.
Para aquellos, vea las respuestas a:
- ¿Por qué Curiosity tiene dos imágenes de sí mismo, o una es un código QR?
- esta respuesta a ¿Se han utilizado códigos de barras “QR” u otros códigos de barras 2D en vuelos espaciales?


Engineering interns Tristan Schuler, left, and Greta Studier pose with 2D barcodes and a Nano Air-Bearing Simulator prototype that uses the navigation system they developed while at Marshall. Their navigation system is available as open source code on code.nasa.gov. Credits: NASA/Emmett Given