
Los humanos pasaron los últimos cinco milenios y medio inventando más de 100 formas diferentes de escribir números.
Con el debido respeto a los números romanos , la técnica favorita del mundo en este momento es, por un amplio margen, el sistema decimal moderno . Sus usuarios pueden expresar cualquier número entero que quieran con solo 10 pequeños caracteres: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9.
Pero su computadora adopta otro enfoque.
Las computadoras portátiles, los teléfonos inteligentes y otros dispositivos se basan en código binario . Un lenguaje matemático, el binario transmite instrucciones a estos artilugios de alta tecnología. Le dice a su computadora cómo suena la voz de un podcaster, qué colores deben aparecer en un video de YouTube y cuántas letras se usaron en ese correo electrónico que acaba de enviar su jefe.
Sabes. Cosas importantes como esa.
El código binario hace honor a su nombre. A diferencia del sistema decimal, solo utiliza dos tipos de dígitos, que los programadores llaman " bits ". Por lo general, hay "0" y hay "1". Y eso es todo.
Hoy, le mostraremos cómo convertir un número binario en el sistema decimal más familiar. Luego, como buen mago , haremos exactamente lo contrario.
No te preocupes. Con un poco de paciencia, puedes dominar este "truco" y divertirte haciéndolo.
Conozca sus exponentes
Técnicamente, 0 y 1 son los únicos bits que necesitas para escribir números binarios. Pero para darles sentido , debe comprender un tercer valor: 2.
Es mejor si explicamos esto a modo de ejemplo. El número 138 se expresa correctamente en código binario como " 10001010 ".
¿Cómo puede su computadora decir que esta aparente cadena de galimatías significa "138"?
La programación es parte de la respuesta. Alguien le ha informado a su dispositivo que, en este caso, el código binario deletrea un número en lugar de una palabra u oración escrita; hay un método separado para decodificar este último.
Una vez que se establece este hecho básico, el código funciona asignando un exponente diferente de 2 a cada bit individual (es decir, cada 0 y cada 1).
Un exponente es un valor multiplicado por sí mismo un cierto número de veces. Entonces, 2 elevado a la tercera potencia, escrito como 2 3 , es 2 x 2 x 2, que es igual a 8.
Por favor, disfrute de la siguiente lista de poderes de 2 . Confía en nosotros, querrás revisar esto pronto.
2 0 = 1
2 1 = 2
2 2 = 4
2 3 = 8
2 4 = 16
2 5 = 32
2 6 = 64
2 7 = 128
2 8 = 256
2 9 = 512
2 10 = 1024
Conversión de binario a decimal
Ahora volvamos a nuestro número binario original: 10001010
Si el inglés es su lengua materna, prepárese. Estás a punto de luchar contra tus instintos. Mira, el inglés escrito se lee de izquierda a derecha. Pero ahora, tenemos que descomponer ese número binario yendo en la dirección opuesta: de derecha a izquierda.
En cualquier número binario, el bit que está más a la derecha debe multiplicarse por 2 0 . Luego, el que está a su izquierda inmediata se multiplica por 2 1 .
Luego, el bit a su izquierda se multiplica por 2 2 . Y así sucesivamente y así sucesivamente.
¿Notas un patrón aquí? Los exponentes individuales de 2 se utilizan en orden ascendente, de derecha a izquierda .
OK, so now our job is to keep that pattern going until we've matched an exponent of 2 to every bit — every single 0 and 1— in the binary number.
We'll stop once the final bit, the one on the far left side, has been multiplied by the appropriate exponent of 2.
A helpful way to keep your figures straight is to physically line up the exponents over their corresponding binary bits on a sheet of paper. Ideally, it should look something like this:

Good stuff. Alright, now let's return to the actual conversion.
Because 10001010 contains 8 individual bits, we're going to do 8 separate multiplication problems. Let's begin with the 0 on the far right end.
What's 0 x 20? The correct answer is 0.
One problem down, seven to go. Move one space to the left. See the "1" there? Well, 1 x 21 = 2. Now move yet another space to the left. Doing so will give you 0 x 22, which equals 0.
If you continue using this pattern, proceeding from the farthermost right to the farthermost left, here's what you'll ascertain:
0 x 20 = 0
1 x 21 = 2
0 x 22 = 0
1 x 23 = 8
0 x 24 = 0
0 x 25 = 0
0 x 26 = 0
1 x 27 = 128
Hang on, we're almost at the finish line!
Take the results of all those multiplication problems and add them together. Not multiply, add. Savvy?
What does 0 + 2 + 0 + 8 + 0 + 0 + 0 + 128 equal?
Before we answer that, let's get rid of all those zeroes. We don't need them in an addition problem. All we really have to do is solve this puzzle:
2 + 8 + 128 = ?
Guess what? The final answer is 138. Congratulations, we've come full circle! Go take a victory lap.
Note that 138 is a whole number. There is a technique for converting numbers with a fractional component, like 0.25 and 3.14, into binary. But full disclosure: It's kind of complicated. If that doesn't bother you and you'd like to learn more, the Institute of Electrical and Electronics Engineers (IEEE) has published a standardized conversion method.
Here is a handy widget to help you with the conversions.
Converting Decimal to Binary
Having changed "10001010" into "138," it's time to reverse our process. Suppose you'd started out with 138 and had to convert it to binary. How would you do it?
Once again, exponents are the key to the whole shebang.
Have another look at our "powers of 2" list. Find the value that comes the closest to 138 without exceeding it.
A quick reread tells us 138 sits between 256 (which is 28) and 128 (that's 27).
Now, we're going to subtract 128 from 138. Here's the equation:
138 - 128 = 10
Next, take that 10 and have a second gander at the exponent list. The power of 2 which comes the closest to equaling 10 is 23, or 8. So at this point, our job is to subtract 8 from 10. Like so:
10 - 8 = 2
And what do you know? The number 2 is equal to 21.
This process gave us three important figures: 128, 8 and 2. Our next objective is to add them up.
128 + 8 + 2 = 138.
Find a piece of paper if you haven't already done so. Write out the value of every exponent of 2 beginning with "128" (remember, that's 27) and "1" (which equals 20). Do this in descending order from left to right. And make sure to leave some space between each number.
Your scribbling should look like this:
128 64 32 16 8 4 2 1
As you can see, there are eight individual values listed here. Draw a downward-pointing arrow (↓) below each value.
Then, consult the addition problem we wrote down up above, the one that says 128 + 8 + 2 = 138
Do you see a "128" in that problem? If so, write a "1" underneath the corresponding arrow. Is there a "64" written in the equation? Nope! So beneath that arrow, we're going to write a "0." Keep to the same pattern and you'll get this:
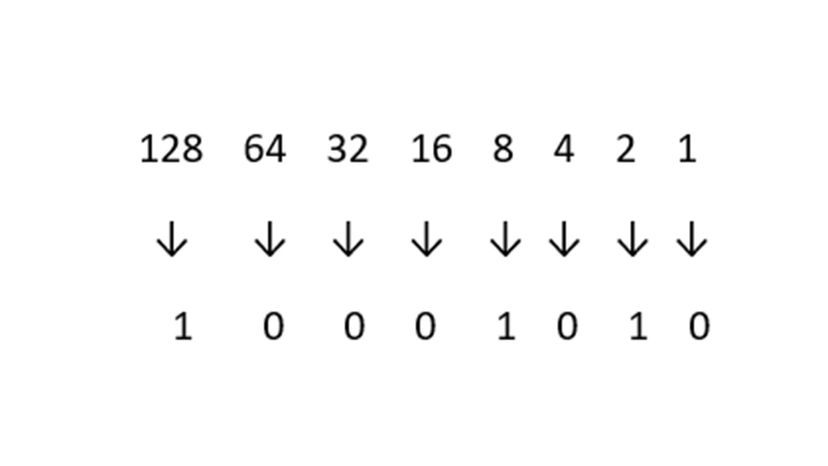
Look familiar? We're left with 10001010 — and as we've already established, that means "138."
So there you go. Our proverbial magician has made the rabbit disappear and brought it back again. Carrots all around!
Now That's Funny
A la popular serie de comedia de ciencia ficción "Futurama" le encantan los chistes matemáticos. En el episodio de la segunda temporada "The Honking", una mansión embrujada es legada al robot sinvergüenza, Bender Bending Rodriguez. Cuando entra, está aterrorizado al descubrir un mensaje binario secreto que dice "1010011010". Quizás Bender tenía razón al estar asustado; en forma decimal, eso se traduce como "666".















































