Stern-Brocot 트리를 더 나은 수렴을 위해 사용할 수 있습니까? $2^m/3^n$?
필수 읽기 :
- 양의 실수는 다음과 같이 근사 할 수 있습니까? $2^m/3^n$ 와 $(m,n)$ 충분히 큰?
- Stern Brocot 트리 시퀀스
이 단점이없는 절차, 즉 다음 근사값이 항상 원하는 결과에 더 가까운 절차를 찾고있는 이유. 이것이 내가 지금까지 시도한 것입니다.
질문 (2.)에 따르면 모든 양의 실수에 대해$0 \lt g \lt 1$, Stern Brocot 트리 [..]에는 실수로 수렴하는 무한한 시퀀스가 있습니다. 한편이 질문에는 답 이 있으며 그 결과의 주요 결과는 다음과 같습니다. $$ - \frac{1}{n_1(n_1+n_2)} \lt g - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} $$ 질문 (1.)을 감안하여 $\ln(2)/\ln(3)$ 그 숫자를 위해 $g$. 그런 다음 다음과 같습니다. $$ - \frac{1}{n_1(n_1+n_2)} \lt \frac{\ln(2)}{\ln(3)} - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} \\ - \frac{\ln(3)}{n_1} \lt \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \lt + \frac{\ln(3)}{n_2} \\ \ln\left(3^{-1/n_1}\right) \lt \ln\left(\frac{2^{n_1+n_2}}{3^{m_1+m_2}}\right) \lt \ln\left(3^{+1/n_2}\right) \\ 3^{-1/n_1} \lt \frac{2^{n_1+n_2}}{3^{m_1+m_2}} \lt 3^{+1/n_2} $$Stern-Brocot 트리를 통한 검색을 그림으로 그릴 수 있습니다. 파란색 선이 기능입니다. $\,\color{blue}{x\ln(2)-y\ln(3)=0}\,$, 작은 원은 격자에 매핑 된 분수입니다. $\,m/n \to (m,n)\,$, 엄청나게 검은 색으로 채워진 점은 Stern-Brocot 트리의 분수입니다. 트리를 검색하는 것이 증가하는 것보다 훨씬 더 효율적이라는 것을 알 수 있습니다. $m$ 과 $n$ 한 번에 하나씩 증가합니다.
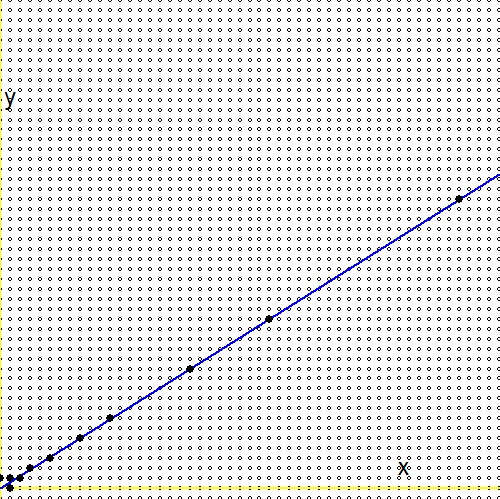
이제 위 공식의 두 번째 줄에있는 표현식을 참조 (1)의 유사한 표현식과 비교합니다. $$ \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \quad \Longleftrightarrow \quad m\ln(2) - n\ln(3) - \ln(r) $$ 그리고 실망에 대비하십시오 : 임의의 실수의 로그 $r$누락! 또는 :$\ln(r)=0$ 또는 $r=1$. 이것은 Stern-Brocot 트리를 통한 우리의 "무한 검색"이 매우 효율적이기는하지만 마침내 숫자 1에 대한 근사치에 도달한다는 것을 의미합니다. 나는 이것이 이상하다고 생각합니다. 왜냐하면-그래픽 적으로-사이에 큰 차이가없는 것 같기 때문입니다$\color{red}{2^m/3^n \to r}$ 과 $\color{blue}{2^m/3^n \to 1}$:
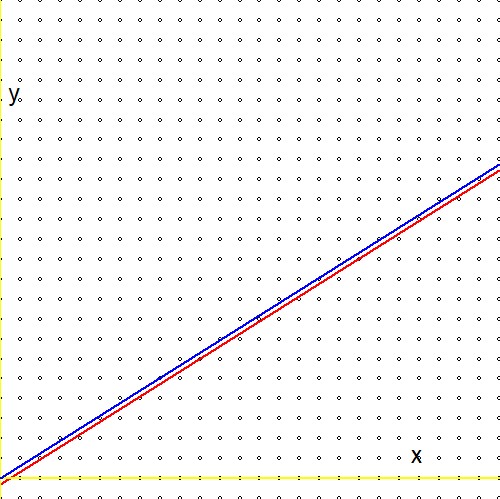
따라서 질문 : Stern-Brocot 절차를 조정하여 하나가 아닌 다른 실제에 대해 작동하는 방법이 있습니까?
편집하다.
여기 Q & A의 유사한 그림과 비교하여 Stern-Brocot 방법으로 놀라운 수렴을 보여주는 또 다른 그래프가 있습니다.$2^m/3^n$ 와 $(m,n)$충분히 큰? :
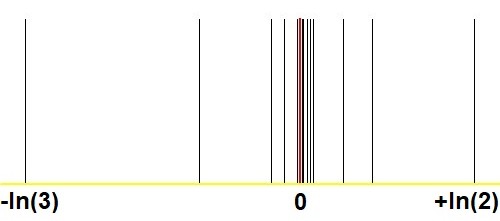
답변
Stern-Brocot 절차를 사용하지 않는 접근 방식을 제공하겠습니다.
보여 주면 충분합니다. $\frac{2^{m}}{3^{n}}$간격 [1,2]에서 조밀합니다. 복용 이후$\alpha\in (0,\infty)$ 이 간격을 벗어나면 $k\in Z$ 그래서 $\alpha = 2^{k}\gamma $ 일부 $\gamma \in [1,2]$. 그런 다음 우리는$\frac{2^{m}}{3^{n}}$ 어떤 접근 $\gamma$, 시퀀스를 항으로 곱하면 $2^{k}$ (아마도 시퀀스의 꼬리를 취함), 우리는 시퀀스를 얻습니다. $\frac{2^{m}}{3^{n}}$ 어떤 접근 $\alpha$.
다음으로지도가 $f:[1,2] -> [0,1]$ 와 $f(x) = log_{2}(x)$ 은사입니다.
이미지 $\frac{2^{m}}{3^{n}}$ 지도 아래는 $N-Nlog_{2}(3)$. 그래서 그것을 보여주는 것으로 충분합니다$N-Nlog_{2}(3)$ 밀도가 높다 $[0,1]$.
이것은 Ergodic 정리의 특별한 경우 인 Weyl의 등분 포 정리의 결과입니다.
중히 여기다 $a=2-log_{2}(3) = log_{2}(\frac{4}{3})$, 그래서 $a$ 세트의 이미지에 있으므로 $na = log_{2}(\frac{4^{n}}{3^{n}})$ 그래서 분수 부분입니다 $na$.
weyl Equidistribution 정리 (사소한 결과가 아님)는 비합리적 a의 분수 부분을 보여줍니다. $na$균일하게 분포되어 있으므로 [0,1]에 조밀합니다. 이후$2-log_{2}(3)$ 이 정리를 사용할 수 있습니다.