Stern-Brocot ağacı, daha iyi yakınsama için kullanılabilir mi? $2^m/3^n$?
Önkoşul okuma:
- Herhangi bir pozitif gerçek şu şekilde yaklaştırılabilir mi? $2^m/3^n$ ile $(m,n)$ yeterince geniş?
- Stern Brocot ağacı dizisi
Bu dezavantajı olmayan, yani bir sonraki yaklaşımın her zaman istenen sonuca daha yakın olduğu bir prosedür aradığımın nedeni. Şimdiye kadar denediğim şey bu.
Soru (2.) 'ye göre, her pozitif gerçek sayı için$0 \lt g \lt 1$, Stern Brocot ağacında [..] gerçek sayıya yakınsayan sonsuz bir dizi vardır. Bu arada, bu sorunun bir cevabı var ve oradaki ana sonuç şu şekildedir: $$ - \frac{1}{n_1(n_1+n_2)} \lt g - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} $$ Soru (1.) göz önüne alındığında, yerine $\ln(2)/\ln(3)$ bu numara için $g$. Ardından şunu takip eder: $$ - \frac{1}{n_1(n_1+n_2)} \lt \frac{\ln(2)}{\ln(3)} - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} \\ - \frac{\ln(3)}{n_1} \lt \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \lt + \frac{\ln(3)}{n_2} \\ \ln\left(3^{-1/n_1}\right) \lt \ln\left(\frac{2^{n_1+n_2}}{3^{m_1+m_2}}\right) \lt \ln\left(3^{+1/n_2}\right) \\ 3^{-1/n_1} \lt \frac{2^{n_1+n_2}}{3^{m_1+m_2}} \lt 3^{+1/n_2} $$Stern-Brocot ağacındaki arama resmedilebilir. Mavi çizgi işlevdir $\,\color{blue}{x\ln(2)-y\ln(3)=0}\,$, küçük daireler kesirlerdir, bir ızgara üzerinde eşlenir $\,m/n \to (m,n)\,$, Stern-Brocot ağacındaki büyük siyah dolgulu noktalar fraksiyonlardır. Ağaçta aramanın artırmaya göre çok daha verimli olduğu görülüyor. $m$ ve $n$ her seferinde bir artışla.
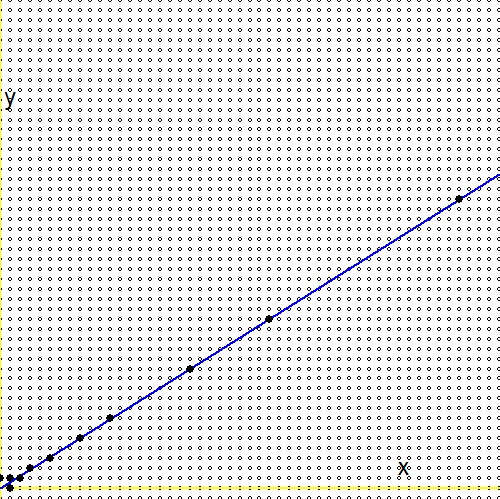
Şimdi yukarıdaki formüllerin ikinci satırındaki ifadeyi referans (1) 'deki benzer bir ifade ile karşılaştırın: $$ \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \quad \Longleftrightarrow \quad m\ln(2) - n\ln(3) - \ln(r) $$ Ve bir hayal kırıklığına hazırlıklı olun: keyfi gerçekliğin logaritması $r$kayıp! Veya alternatif olarak:$\ln(r)=0$ veya $r=1$. Bu, Stern-Brocot ağacındaki "sonsuz araştırmamız", son derece verimli olmasına rağmen, sonunda yalnızca bir numara için bir yaklaşıma ulaştığı anlamına gelir. Bunu garip buluyorum çünkü - grafiksel olarak - arasında büyük bir fark yok gibi görünüyor$\color{red}{2^m/3^n \to r}$ ve $\color{blue}{2^m/3^n \to 1}$:
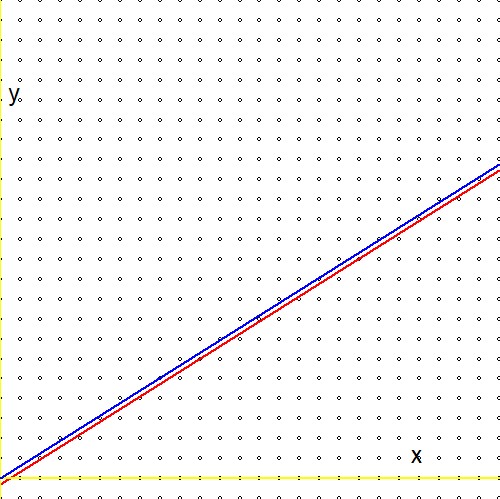
Dolayısıyla SORU: Stern-Brocot prosedürünü birden fazla gerçek için işe yarayacak şekilde uyarlamanın bir yolu var mı?
DÜZENLE.
İşte Stern-Brocot yöntemiyle şaşırtıcı yakınsamayı, Soru-Cevap bölümümdeki benzer resimlerle karşılaştırmalı olarak gösteren başka bir grafik geliyor. Herhangi bir pozitif gerçek$2^m/3^n$ ile $(m,n)$yeterince geniş? :
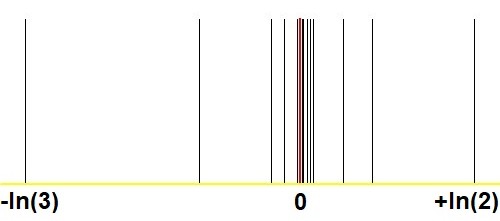
Yanıtlar
Stern-Brocot prosedürünü kullanmayan bir yaklaşım sunacağım.
Bunu göstermek yeterli $\frac{2^{m}}{3^{n}}$[1,2] aralığında yoğundur. Aldığından beri$\alpha\in (0,\infty)$ bu aralığın dışında biraz var $k\in Z$ Böylece $\alpha = 2^{k}\gamma $ bazı $\gamma \in [1,2]$. O zaman bir dizi olduğunu biliyoruz$\frac{2^{m}}{3^{n}}$ hangi yaklaşımlar $\gamma$, diziyi terimsel olarak çarparak $2^{k}$ (muhtemelen dizinin bir kuyruğunu alarak), bir dizi elde ederiz $\frac{2^{m}}{3^{n}}$ hangi yaklaşımlar $\alpha$.
Sonra haritanın $f:[1,2] -> [0,1]$ ile $f(x) = log_{2}(x)$ bir bijeksiyondur.
Resmi $\frac{2^{m}}{3^{n}}$ haritanın altında $N-Nlog_{2}(3)$. Yani bunu göstermek yeterli$N-Nlog_{2}(3)$ yoğun $[0,1]$.
Bu, Ergodik teoremin özel bir durumu olan Weyl'in Eş dağılım teoreminin bir sonucudur.
Düşünmek $a=2-log_{2}(3) = log_{2}(\frac{4}{3})$, yani $a$ setin görüntüsünde, Öyleyse $na = log_{2}(\frac{4^{n}}{3^{n}})$ ve böylelikle kesirli kısmı $na$.
Weyl Eş dağılım teoremi (önemsiz bir sonuç değildir), irrasyonel bir $na$düzgün dağılmıştır ve bu nedenle [0,1] üzerinde yoğundur. Dan beri$2-log_{2}(3)$ irrasyoneldir bu teoremi kullanabilirsiniz.