A árvore de Stern-Brocot pode ser empregada para uma melhor convergência de $2^m/3^n$?
Pré-requisito de leitura:
- Qualquer real positivo pode ser aproximado como$2^m/3^n$com$(m,n)$grande o suficiente?
- Sequência da árvore Stern Brocot
Razão pela qual tenho procurado um procedimento que não tenha esse inconveniente, ou seja, onde a próxima aproximação seja sempre mais próxima do resultado desejado. Isto é o que eu tentei até agora.
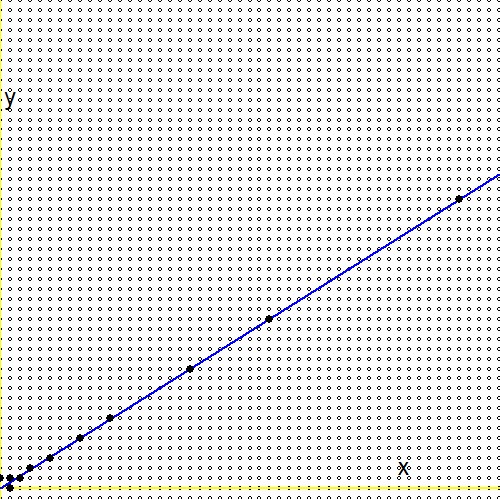
De acordo com a questão (2.), para todo número real positivo$0 \lt g \lt 1$, existe uma sequência infinita na árvore Stern Brocot [ .. ] que converge para o número real. Enquanto isso, esta pergunta tem uma resposta , e o resultado principal é o seguinte: $$ - \frac{1}{n_1(n_1+n_2)} \lt g - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} $$Em vista da questão (1.), substituímos $\ln(2)/\ln(3)$para esse número $g$. Então segue que: $$ - \frac{1}{n_1(n_1+n_2)} \lt \frac{\ln(2)}{\ln(3)} - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} \\ - \frac{\ln(3)}{n_1} \lt \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \lt + \frac{\ln(3)}{n_2} \\ \ln\left(3^{-1/n_1}\right) \lt \ln\left(\frac{2^{n_1+n_2}}{3^{m_1+m_2}}\right) \lt \ln\left(3^{+1/n_2}\right) \\ 3^{-1/n_1} \lt \frac{2^{n_1+n_2}}{3^{m_1+m_2}} \lt 3^{+1/n_2} $$A busca pela árvore Stern-Brocot pode ser retratada. A linha azul é a função $\,\color{blue}{x\ln(2)-y\ln(3)=0}\,$, pequenos círculos são frações, mapeadas em uma grade $\,m/n \to (m,n)\,$, pontos preenchidos maciçamente pretos são as frações na árvore Stern-Brocot. Vê-se que pesquisar na árvore é muito mais eficiente do que aumentar $m$e $n$com incrementos um de cada vez.
Agora compare a expressão na segunda linha das fórmulas acima com uma expressão análoga na referência (1.):$$ \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \quad \Longleftrightarrow \quad m\ln(2) - n\ln(3) - \ln(r) $$E esteja preparado para uma decepção: o logaritmo do real arbitrário$r$está desaparecido! Ou alternativamente:$\ln(r)=0$ou$r=1$. Isso significa que nossa "busca infinita" pela árvore Stern-Brocot, embora altamente eficiente, finalmente chega a uma aproximação apenas para o número um. Acho isso estranho, porque - graficamente - não parece haver uma grande diferença entre$\color{red}{2^m/3^n \to r}$e$\color{blue}{2^m/3^n \to 1}$:
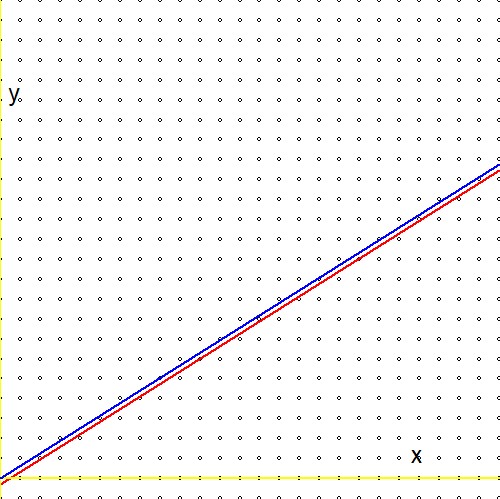
Daí a PERGUNTA: existe algum meio de adaptar o procedimento Stern-Brocot para que funcione para outros reais?
EDITAR.
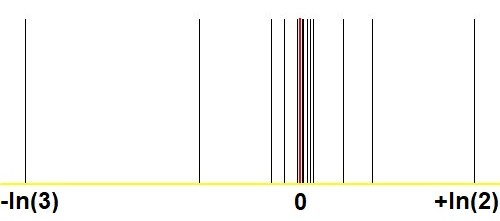
Aqui vem outro gráfico que mostra a surpreendente convergência com o método Stern-Brocot, em comparação com imagens análogas em minhas perguntas e respostas .$2^m/3^n$com$(m,n)$grande o suficiente? :
Respostas
Vou dar uma abordagem que não usa o procedimento Stern-Brocot.
Basta mostrar que$\frac{2^{m}}{3^{n}}$é denso no intervalo [1,2]. Desde que tomou$\alpha\in (0,\infty)$fora deste intervalo existe algum$k\in Z$de modo a$\alpha = 2^{k}\gamma $para alguns$\gamma \in [1,2]$. Então sabemos que existe uma sequência em$\frac{2^{m}}{3^{n}}$que se aproxima$\gamma$, multiplicando a sequência termo a termo por$2^{k}$(possivelmente tomando uma cauda da sequência), obtemos uma sequência em$\frac{2^{m}}{3^{n}}$que se aproxima$\alpha$.
Em seguida, considere que o mapa$f:[1,2] -> [0,1]$com$f(x) = log_{2}(x)$é uma bijeção.
A imagem de$\frac{2^{m}}{3^{n}}$sob o mapa é$N-Nlog_{2}(3)$. Então é suficiente mostrar que$N-Nlog_{2}(3)$é denso em$[0,1]$.
Esta é uma consequência do teorema da equidistribuição de Weyl, que é um caso especial do teorema ergódico.
Considerar$a=2-log_{2}(3) = log_{2}(\frac{4}{3})$, assim$a$está na imagem do conjunto, Então é$na = log_{2}(\frac{4^{n}}{3^{n}})$e assim é a parte fracionária de$na$.
O teorema da equidistribuição de Weyl (que não é um resultado trivial) mostra que para a irracional a parte fracionária de$na$é uniformemente distribuído e, portanto, denso em [0,1]. Desde$2-log_{2}(3)$é irracional, você pode usar este teorema.