A matemática de ponto flutuante está quebrada?

Question

Considere o seguinte código:

0.1 + 0.2 == 0.3  ->  false

0.1 + 0.2         ->  0.30000000000000004

Por que essas imprecisões acontecem?

Answer 1

A matemática de ponto flutuante binário é assim. Na maioria das linguagens de programação, ele é baseado no padrão IEEE 754 . O ponto crucial do problema é que os números são representados nesse formato como um número inteiro vezes uma potência de dois; números racionais (como 0.1, que é 1/10) cujo denominador não é uma potência de dois não podem ser representados exatamente.

Pois 0.1no binary64formato padrão , a representação pode ser escrita exatamente como

• 0.1000000000000000055511151231257827021181583404541015625 em decimal, ou
• 0x1.999999999999ap-4em notação hexfloat C99 .

Em contraste, o número racional 0.1, que é 1/10, pode ser escrito exatamente como

• 0.1 em decimal, ou
• 0x1.99999999999999...p-4em um análogo da notação hexfloat C99, onde o ...representa uma sequência interminável de 9's.

As constantes 0.2e 0.3em seu programa também serão aproximações de seus valores reais. Acontece que o mais próximo doublede 0.2é maior do que o número racional, 0.2mas o mais próximo doublede 0.3é menor que o número racional 0.3. A soma de 0.1e 0.2acaba sendo maior do que o número racional 0.3e, portanto, discordando da constante em seu código.

Um tratamento bastante abrangente de questões aritméticas de ponto flutuante é o que todo cientista da computação deve saber sobre aritmética de ponto flutuante . Para uma explicação mais fácil de digerir, consulte floating-point-gui.de .

Nota lateral: Todos os sistemas numéricos posicionais (base N) compartilham este problema com precisão

Números decimais simples (base 10) têm os mesmos problemas, e é por isso que números como 1/3 terminam em 0,3333333333 ...

Você acabou de descobrir um número (3/10) que é fácil de representar com o sistema decimal, mas não se encaixa no sistema binário. Pode ser em ambos os sentidos (em um pequeno grau) também: 1/16 é um número feio em decimal (0,0625), mas em binário parece tão bom quanto um 10.000 em decimal (0,0001) ** - se estivéssemos em o hábito de usar um sistema numérico de base 2 em nossas vidas diárias, você até olhava para esse número e instintivamente entenderia que poderia chegar lá reduzindo algo pela metade, reduzindo pela metade novamente, e novamente e novamente.

** Claro, não é exatamente assim que os números de ponto flutuante são armazenados na memória (eles usam uma forma de notação científica). No entanto, ele ilustra o ponto de que erros binários de precisão de ponto flutuante tendem a surgir porque os números do "mundo real" com os quais estamos geralmente interessados ​​em trabalhar são frequentemente potências de dez - mas apenas porque usamos um sistema numérico decimal dia- hoje. É também por isso que diremos coisas como 71% em vez de "5 de cada 7" (71% é uma aproximação, já que 5/7 não pode ser representado exatamente com nenhum número decimal).

Portanto, não: os números de ponto flutuante binários não são quebrados, eles simplesmente são tão imperfeitos quanto qualquer outro sistema numérico de base N :)

Nota lateral lateral: Trabalhando com flutuadores na programação

Na prática, este problema de precisão significa que você precisa usar funções de arredondamento para arredondar seus números de ponto flutuante para quantas casas decimais você estiver interessado antes de exibi-los.

Você também precisa substituir os testes de igualdade por comparações que permitem alguma tolerância, o que significa:

Você não fazerif (x == y) { ... }

Em vez disso, faça if (abs(x - y) < myToleranceValue) { ... }.

onde absestá o valor absoluto. myToleranceValueprecisa ser escolhido para sua aplicação específica - e isso terá muito a ver com quanto "espaço de manobra" você está preparado para permitir e qual pode ser o maior número que você vai comparar (devido a problemas de perda de precisão ) Cuidado com as constantes de estilo "epsilon" no idioma de sua escolha. Eles não devem ser usados ​​como valores de tolerância.

Answer 2

A perspectiva de um designer de hardware

Acredito que devo adicionar a perspectiva de um designer de hardware a isso, já que projeto e construo hardware de ponto flutuante. Saber a origem do erro pode ajudar a entender o que está acontecendo no software e, em última análise, espero que isso ajude a explicar as razões pelas quais os erros de ponto flutuante acontecem e parecem se acumular com o tempo.

1. Visão Geral

De uma perspectiva de engenharia, a maioria das operações de ponto flutuante terá algum elemento de erro, já que o hardware que faz os cálculos de ponto flutuante só precisa ter um erro de menos da metade de uma unidade no último lugar. Portanto, muito hardware irá parar em uma precisão que só é necessária para produzir um erro de menos da metade de uma unidade no último lugar para uma única operação que é especialmente problemática na divisão de ponto flutuante. O que constitui uma única operação depende de quantos operandos a unidade leva. Para a maioria, é dois, mas algumas unidades levam 3 ou mais operandos. Por causa disso, não há garantia de que operações repetidas resultarão em um erro desejável, pois os erros aumentam com o tempo.

2. Padrões

A maioria dos processadores segue o padrão IEEE-754 , mas alguns usam padrões desnormalizados ou diferentes. Por exemplo, há um modo desnormalizado no IEEE-754 que permite a representação de números de ponto flutuante muito pequenos em detrimento da precisão. O seguinte, no entanto, cobrirá o modo normalizado do IEEE-754, que é o modo típico de operação.

No padrão IEEE-754, os designers de hardware têm permissão para qualquer valor de erro / epsilon, desde que seja menos da metade de uma unidade no último lugar, e o resultado só precisa ser menos da metade de uma unidade no último lugar para uma operação. Isso explica por que, quando há operações repetidas, os erros se somam. Para a precisão dupla IEEE-754, este é o 54º bit, já que 53 bits são usados ​​para representar a parte numérica (normalizada), também chamada de mantissa, do número de ponto flutuante (por exemplo, 5.3 em 5.3e5). As próximas seções fornecem mais detalhes sobre as causas dos erros de hardware em várias operações de ponto flutuante.

3. Causa do erro de arredondamento na divisão

A principal causa do erro na divisão de ponto flutuante são os algoritmos de divisão usados ​​para calcular o quociente. A maioria dos sistemas de computador calcular divisão usando a multiplicação por uma inversa, principalmente em Z=X/Y, Z = X * (1/Y). Uma divisão é calculada iterativamente, ou seja, cada ciclo calcula alguns bits do quociente até que a precisão desejada seja atingida, que para o IEEE-754 é qualquer coisa com um erro menor que uma unidade no último lugar. A tabela de recíprocos de Y (1 / Y) é conhecida como a tabela de seleção de quociente (QST) na divisão lenta, e o tamanho em bits da tabela de seleção de quociente é geralmente a largura da raiz, ou um número de bits de o quociente calculado em cada iteração, mais alguns bits de guarda. Para o padrão IEEE-754, precisão dupla (64 bits), seria o tamanho da raiz do divisor, mais alguns bits de guarda k, onde k>=2. Então, por exemplo, uma Tabela de Seleção de Quociente típica para um divisor que calcula 2 bits do quociente por vez (raiz 4) seria 2+2= 4bits (mais alguns bits opcionais).

3.1 Erro de arredondamento de divisão: Aproximação de recíproca

Os recíprocos na tabela de seleção de quocientes dependem do método de divisão : divisão lenta, como a divisão SRT, ou divisão rápida, como a divisão Goldschmidt; cada entrada é modificada de acordo com o algoritmo de divisão em uma tentativa de produzir o menor erro possível. Em qualquer caso, porém, todos os recíprocos são aproximações do recíproco real e introduzem algum elemento de erro. Os métodos de divisão lenta e divisão rápida calculam o quociente iterativamente, ou seja, alguns números de bits do quociente são calculados a cada etapa, então o resultado é subtraído do dividendo, e o divisor repete as etapas até que o erro seja inferior a metade de um unidade em último lugar. Os métodos de divisão lenta calculam um número fixo de dígitos do quociente em cada etapa e geralmente são mais baratos de construir, e os métodos de divisão rápida calculam um número variável de dígitos por etapa e geralmente são mais caros de construir. A parte mais importante dos métodos de divisão é que a maioria deles depende da multiplicação repetida por uma aproximação de um recíproco, portanto, estão sujeitos a erros.

4. Erros de arredondamento em outras operações: truncamento

Outra causa dos erros de arredondamento em todas as operações são os diferentes modos de truncamento da resposta final que o IEEE-754 permite. Há truncar, arredondar para zero, arredondar para o mais próximo (padrão), arredondar para baixo e arredondar para cima. Todos os métodos introduzem um elemento de erro de menos de uma unidade no último lugar para uma única operação. Com o tempo e operações repetidas, o truncamento também adiciona cumulativamente ao erro resultante. Esse erro de truncamento é especialmente problemático na exponenciação, que envolve alguma forma de multiplicação repetida.

5. Operações repetidas

Como o hardware que faz os cálculos de ponto flutuante só precisa produzir um resultado com um erro de menos da metade de uma unidade no último lugar para uma única operação, o erro aumentará com as operações repetidas se não for observado. Esta é a razão de que em cálculos que requerem um erro limitado, os matemáticos usam métodos como o arredondamento para o dígito par mais próximo no último lugar do IEEE-754, porque, com o tempo, os erros são mais propensos a se cancelarem out e Interval Arithmetic combinada com variações dos modos de arredondamento IEEE 754 para prever erros de arredondamento e corrigi-los. Por causa de seu erro relativo baixo em comparação com outros modos de arredondamento, arredondar para o dígito par mais próximo (no último lugar), é o modo de arredondamento padrão do IEEE-754.

Observe que o modo de arredondamento padrão, arredondado para o dígito par mais próximo na última posição , garante um erro de menos da metade de uma unidade na última posição para uma operação. Usar o truncamento, arredondamento para cima e arredondamento para baixo sozinho pode resultar em um erro maior que a metade de uma unidade no último lugar, mas menos de uma unidade no último lugar, portanto, esses modos não são recomendados, a menos que sejam usado na Aritmética de Intervalo.

6. Resumo

Em suma, a razão fundamental para os erros em operações de ponto flutuante é uma combinação do truncamento no hardware e o truncamento de um recíproco no caso de divisão. Visto que o padrão IEEE-754 requer apenas um erro de menos da metade de uma unidade no último lugar para uma única operação, os erros de ponto flutuante em operações repetidas serão somados, a menos que sejam corrigidos.

Answer 3

Ele é quebrado exatamente da mesma forma que a notação decimal (base 10) é quebrada, apenas para a base 2.

Para entender, pense em representar 1/3 como um valor decimal. É impossível fazer exatamente! Da mesma forma, 1/10 (decimal 0,1) não pode ser representado exatamente na base 2 (binária) como um valor "decimal"; um padrão repetido após o ponto decimal continua para sempre. O valor não é exato e, portanto, você não pode fazer matemática exata com ele usando métodos normais de ponto flutuante.

Answer 4

A maioria das respostas aqui aborda essa questão em termos técnicos muito secos. Eu gostaria de abordar isso em termos que seres humanos normais possam entender.

Imagine que você está tentando fatiar pizzas. Você tem um cortador de pizza robótico que pode cortar fatias de pizza exatamente pela metade. Pode cortar pela metade uma pizza inteira ou pode cortar pela metade uma fatia existente, mas em qualquer caso, a metade é sempre exata.

Esse cortador de pizza tem movimentos muito finos, e se você começar com uma pizza inteira, depois dividi-la pela metade e continuar cortando pela metade a menor fatia de cada vez, você pode fazer a redução pela metade 53 vezes antes que a fatia fique pequena demais até mesmo para suas habilidades de alta precisão . Nesse ponto, você não pode mais reduzir pela metade essa fatia muito fina, mas deve incluí-la ou excluí-la como está.

Agora, como você dividiria todas as fatias de forma que somassem um décimo (0,1) ou um quinto (0,2) de uma pizza? Realmente pense sobre isso e tente descobrir. Você pode até tentar usar uma pizza de verdade, se tiver um cortador de pizza de precisão mítico à mão. :-)

---

A maioria dos programadores experientes, é claro, sabe a verdadeira resposta, que é que não há como juntar um décimo ou quinto exato da pizza usando essas fatias, não importa o quão finas sejam as fatias. Você pode fazer uma boa aproximação, e se somar a aproximação de 0,1 com a aproximação de 0,2, você obtém uma aproximação muito boa de 0,3, mas ainda é apenas isso, uma aproximação.

Para números de precisão dupla (que é a precisão que permite reduzir a pizza pela metade 53 vezes), os números imediatamente menores e maiores que 0,1 são 0,09999999999999999167332731531132594682276248931884765625 e 0,1000000000000000055511151231257827021181583404541015625. O último é um pouco mais próximo de 0,1 do que o primeiro, então um analisador numérico irá, dada uma entrada de 0,1, favorecer o último.

(A diferença entre esses dois números é a "menor fatia" que devemos decidir incluir, que introduz uma tendência para cima, ou excluir, que introduz uma tendência para baixo. O termo técnico para a menor fatia é ulp .)

No caso de 0,2, os números são todos iguais, apenas aumentados por um fator de 2. Mais uma vez, favorecemos o valor que é ligeiramente superior a 0,2.

Observe que, em ambos os casos, as aproximações de 0,1 e 0,2 têm uma ligeira tendência para cima. Se somarmos o suficiente desses vieses, eles empurrarão o número cada vez mais para longe do que queremos e, de fato, no caso de 0,1 + 0,2, o viés é alto o suficiente para que o número resultante não seja mais o número mais próximo a 0,3.

Em particular, 0,1 + 0,2 é realmente 0,1000000000000000055511151231257827021181583404541015625 + 0,200000000000000011102230246251565404236316680908203125 = 0,300000000000000044408920985006261616945267797599679968917683689179683689179236328125, enquanto que o número 9376891796899917968993391796891796899339179689339179683985999178999 943689339 mais próximo de 948812599968999139689995913689179689179689179689179689179236328125.

---

PS Algumas linguagens de programação também fornecem cortadores de pizza que podem dividir fatias em décimos exatos . Embora esses cortadores de pizza sejam incomuns, se você tiver acesso a um, deverá usá-lo quando for importante conseguir obter exatamente um décimo ou um quinto de uma fatia.

(Postado originalmente no Quora.)

Answer 5

Erros de arredondamento de ponto flutuante. 0,1 não pode ser representado com tanta precisão na base 2 como na base 10 devido à falta do fator primo de 5. Assim como 1/3 leva um número infinito de dígitos para representar em decimal, mas é "0,1" na base 3, 0,1 leva um número infinito de dígitos na base 2, onde não na base 10. E os computadores não têm uma quantidade infinita de memória.

Answer 6

Além das outras respostas corretas, você pode considerar escalar seus valores para evitar problemas com aritmética de ponto flutuante.

Por exemplo:

var result = 1.0 + 2.0;     // result === 3.0 returns true

... ao invés de:

var result = 0.1 + 0.2;     // result === 0.3 returns false

A expressão 0.1 + 0.2 === 0.3retorna falseem JavaScript, mas felizmente a aritmética de inteiros em ponto flutuante é exata, portanto, os erros de representação decimal podem ser evitados por escalonamento.

Como um exemplo prático, para evitar problemas de ponto flutuante em que a precisão é fundamental, é recomendado ¹ tratar o dinheiro como um número inteiro que representa o número de centavos: 2550centavos em vez de 25.50dólares.

---

¹ Douglas Crockford: JavaScript: As partes boas : Apêndice A - Partes horríveis (página 105) .

Answer 7

Minha resposta é bem longa, então a dividi em três seções. Como a questão é sobre matemática de ponto flutuante, coloquei ênfase no que a máquina realmente faz. Também tornei específico para precisão dupla (64 bits), mas o argumento se aplica igualmente a qualquer aritmética de ponto flutuante.

Preâmbulo

Um número de formato de ponto flutuante binário de precisão dupla IEEE 754 (binary64) representa um número da forma

valor = (-1) ^ s * (1.m ₅₁ m ₅₀ ... m ₂ m ₁ m ₀ ) ₂ * 2 ^e-1023

em 64 bits:

• O primeiro bit é o bit de sinal : 1se o número for negativo, 0caso contrário , ¹ .
• Os próximos 11 bits são o expoente , que é deslocado por 1023. Em outras palavras, depois de ler os bits do expoente de um número de precisão dupla, 1023 deve ser subtraído para obter a potência de dois.
• Os 52 bits restantes são o significando (ou mantissa). No mantissa, um 'implícita' 1.é sempre ² omitido uma vez que o bit mais significativo de qualquer valor binário é 1.

¹ - IEEE 754 permite o conceito de zero com sinal - +0e -0são tratados de forma diferente: 1 / (+0)é infinito positivo; 1 / (-0)é infinito negativo. Para valores zero, os bits de mantissa e expoente são todos zero. Nota: os valores zero (+0 e -0) não são explicitamente classificados como denormal ² .

² - Este não é o caso de números denormais , que têm um expoente de deslocamento de zero (e um implícito 0.). O intervalo de números de precisão dupla denormal é d _min ≤ | x | ≤ d _max , onde d _min (o menor número não zero representável) é 2 ^{-1023 - 51} (≈ 4,94 * 10 ^-324 ) ed _max (o maior número denormal, para o qual a mantissa consiste inteiramente de 1s) é 2 ^{-1023 + 1} - 2 ^{-1023 - 51} (≈ 2,225 * 10 ^-308 ).

---

Transformando um número de precisão dupla em binário

Muitos conversores online existem para converter um número de ponto flutuante de precisão dupla em binário (por exemplo, em binaryconvert.com ), mas aqui está um código C # de amostra para obter a representação IEEE 754 para um número de precisão dupla (eu separo as três partes com dois pontos ( :) :

public static string BinaryRepresentation(double value)
{
    long valueInLongType = BitConverter.DoubleToInt64Bits(value);
    string bits = Convert.ToString(valueInLongType, 2);
    string leadingZeros = new string('0', 64 - bits.Length);
    string binaryRepresentation = leadingZeros + bits;

    string sign = binaryRepresentation[0].ToString();
    string exponent = binaryRepresentation.Substring(1, 11);
    string mantissa = binaryRepresentation.Substring(12);

    return string.Format("{0}:{1}:{2}", sign, exponent, mantissa);
}

---

Indo direto ao ponto: a pergunta original

(Vá para o final da versão TL; versão DR)

Cato Johnston (o autor da pergunta) perguntou por que 0,1 + 0,2! = 0,3.

Escrito em binário (com dois pontos separando as três partes), as representações IEEE 754 dos valores são:

0.1 => 0:01111111011:1001100110011001100110011001100110011001100110011010
0.2 => 0:01111111100:1001100110011001100110011001100110011001100110011010

Observe que a mantissa é composta por dígitos recorrentes de 0011. Esta é a chave para a razão de haver qualquer erro nos cálculos - 0,1, 0,2 e 0,3 não podem ser representados em binário precisamente em um número finito de bits binários, mais do que 1/9, 1/3 ou 1/7 podem ser representados precisamente em dígitos decimais .

Observe também que podemos diminuir a potência no expoente em 52 e deslocar o ponto na representação binária para a direita em 52 casas (semelhante a 10 ^-3 * 1,23 == 10 ^-5 * 123). Isso nos permite representar a representação binária como o valor exato que ela representa na forma a * 2 ^p . onde 'a' é um número inteiro.

Converter os expoentes em decimal, remover o deslocamento e adicionar novamente o implícito 1(entre colchetes), 0,1 e 0,2 são:

0.1 => 2^-4 * [1].1001100110011001100110011001100110011001100110011010
0.2 => 2^-3 * [1].1001100110011001100110011001100110011001100110011010
or
0.1 => 2^-56 * 7205759403792794 = 0.1000000000000000055511151231257827021181583404541015625
0.2 => 2^-55 * 7205759403792794 = 0.200000000000000011102230246251565404236316680908203125

Para somar dois números, o expoente precisa ser o mesmo, ou seja:

0.1 => 2^-3 *  0.1100110011001100110011001100110011001100110011001101(0)
0.2 => 2^-3 *  1.1001100110011001100110011001100110011001100110011010
sum =  2^-3 * 10.0110011001100110011001100110011001100110011001100111
or
0.1 => 2^-55 * 3602879701896397  = 0.1000000000000000055511151231257827021181583404541015625
0.2 => 2^-55 * 7205759403792794  = 0.200000000000000011102230246251565404236316680908203125
sum =  2^-55 * 10808639105689191 = 0.3000000000000000166533453693773481063544750213623046875

Como a soma não tem a forma 2 ⁿ * 1. {bbb}, aumentamos o expoente em um e mudamos o ponto decimal ( binário ) para obter:

sum = 2^-2  * 1.0011001100110011001100110011001100110011001100110011(1)
    = 2^-54 * 5404319552844595.5 = 0.3000000000000000166533453693773481063544750213623046875

Agora há 53 bits na mantissa (o 53º está entre colchetes na linha acima). O padrão modo de arredondamento para IEEE 754 é ' Round to mais próxima ' - ou seja, se um número x cai entre dois valores de um e b , o valor onde o bit menos significativo é zero é escolhido.

a = 2^-54 * 5404319552844595 = 0.299999999999999988897769753748434595763683319091796875
  = 2^-2  * 1.0011001100110011001100110011001100110011001100110011

x = 2^-2  * 1.0011001100110011001100110011001100110011001100110011(1)

b = 2^-2  * 1.0011001100110011001100110011001100110011001100110100
  = 2^-54 * 5404319552844596 = 0.3000000000000000444089209850062616169452667236328125

Note-se que um e b diferem apenas no último bit; ...0011+ 1= ...0100. Nesse caso, o valor com o bit menos significativo de zero é b , então a soma é:

sum = 2^-2  * 1.0011001100110011001100110011001100110011001100110100
    = 2^-54 * 5404319552844596 = 0.3000000000000000444089209850062616169452667236328125

enquanto a representação binária de 0,3 é:

0.3 => 2^-2  * 1.0011001100110011001100110011001100110011001100110011
    =  2^-54 * 5404319552844595 = 0.299999999999999988897769753748434595763683319091796875

que difere apenas da representação binária da soma de 0,1 e 0,2 por 2 ^-54 .

A representação binária de 0,1 e 0,2 são as representações mais precisas dos números permitidos pelo IEEE 754. A adição dessas representações, devido ao modo de arredondamento padrão, resulta em um valor que difere apenas no bit menos significativo.

TL; DR

Escrevendo 0.1 + 0.2em uma representação binária IEEE 754 (com dois pontos separando as três partes) e comparando-a 0.3, isto é (coloquei os bits distintos entre colchetes):

0.1 + 0.2 => 0:01111111101:0011001100110011001100110011001100110011001100110[100]
0.3       => 0:01111111101:0011001100110011001100110011001100110011001100110[011]

Convertido de volta para decimal, esses valores são:

0.1 + 0.2 => 0.300000000000000044408920985006...
0.3       => 0.299999999999999988897769753748...

A diferença é exatamente 2 ^-54 , que é ~ 5,5511151231258 × 10 ^-17 - insignificante (para muitas aplicações) quando comparado aos valores originais.

Comparar os últimos bits de um número de ponto flutuante é inerentemente perigoso, como sabe qualquer um que leia o famoso " O que todo cientista da computação deve saber sobre aritmética de ponto flutuante " (que cobre todas as partes principais desta resposta).

A maioria das calculadoras usa dígitos de guarda adicionais para contornar este problema, que é como 0.1 + 0.2daria 0.3: os poucos bits finais são arredondados.

Answer 8

Os números de ponto flutuante armazenados no computador consistem em duas partes, um inteiro e um expoente para o qual a base é levada e multiplicada pela parte inteira.

Se o computador estivesse funcionando na base 10, 0.1estaria 1 x 10⁻¹, 0.2estaria 2 x 10⁻¹e 0.3estaria 3 x 10⁻¹. A matemática inteira é fácil e exata, portanto, adicionar 0.1 + 0.2obviamente resultará em 0.3.

Os computadores geralmente não funcionam na base 10, eles funcionam na base 2. Você ainda pode obter resultados exatos para alguns valores, por exemplo 0.5é 1 x 2⁻¹e 0.25é 1 x 2⁻², e adicioná-los resulta em 3 x 2⁻², ou 0.75. Exatamente.

O problema vem com números que podem ser representados exatamente na base 10, mas não na base 2. Esses números precisam ser arredondados para seu equivalente mais próximo. Assumindo o formato de ponto flutuante IEEE de 64 bits muito comum, o número mais próximo de 0.1é 3602879701896397 x 2⁻⁵⁵e o número mais próximo de 0.2é 7205759403792794 x 2⁻⁵⁵; soma-los resulta em 10808639105689191 x 2⁻⁵⁵, ou um valor decimal exato de 0.3000000000000000444089209850062616169452667236328125. Os números de ponto flutuante geralmente são arredondados para exibição.

Answer 9

Erro de arredondamento de ponto flutuante. Do que todo cientista da computação deve saber sobre aritmética de ponto flutuante :

Comprimir um número infinito de números reais em um número finito de bits requer uma representação aproximada. Embora existam infinitos números inteiros, na maioria dos programas o resultado de cálculos de inteiros pode ser armazenado em 32 bits. Em contraste, dado qualquer número fixo de bits, a maioria dos cálculos com números reais produzirá quantidades que não podem ser representadas exatamente usando tantos bits. Portanto, o resultado de um cálculo de ponto flutuante deve frequentemente ser arredondado para caber de volta em sua representação finita. Este erro de arredondamento é o recurso característico da computação de ponto flutuante.

Answer 10

Minha solução alternativa:

function add(a, b, precision) {
    var x = Math.pow(10, precision || 2);
    return (Math.round(a * x) + Math.round(b * x)) / x;
}

precisão se refere ao número de dígitos que você deseja preservar após a vírgula decimal durante a adição.

Answer 11

Muitas respostas boas foram postadas, mas gostaria de acrescentar mais uma.

Nem todos os números podem ser representados por meio de flutuadores / duplos. Por exemplo, o número "0,2" será representado como "0,2000003" em precisão simples no padrão de ponto flutuante IEEE754.

Modelo para armazenar números reais sob o capô representa números flutuantes como

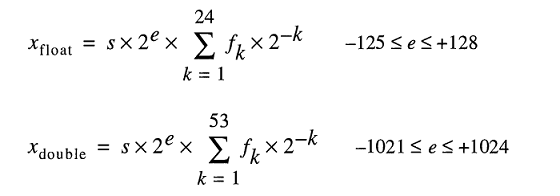
Mesmo que você possa digitar 0.2facilmente, FLT_RADIXe DBL_RADIXé 2; não 10 para um computador com FPU que usa "Padrão IEEE para Aritmética de Ponto Flutuante Binário (ISO / IEEE Std 754-1985)".

Portanto, é um pouco difícil representar esses números com exatidão. Mesmo se você especificar essa variável explicitamente, sem nenhum cálculo intermediário.

Answer 12

Algumas estatísticas relacionadas a esta famosa pergunta de dupla precisão.

Ao adicionar todos os valores ( a + b ) usando uma etapa de 0,1 (de 0,1 a 100), temos ~ 15% de chance de erro de precisão . Observe que o erro pode resultar em valores ligeiramente maiores ou menores. aqui estão alguns exemplos:

0.1 + 0.2 = 0.30000000000000004 (BIGGER)
0.1 + 0.7 = 0.7999999999999999 (SMALLER)
...
1.7 + 1.9 = 3.5999999999999996 (SMALLER)
1.7 + 2.2 = 3.9000000000000004 (BIGGER)
...
3.2 + 3.6 = 6.800000000000001 (BIGGER)
3.2 + 4.4 = 7.6000000000000005 (BIGGER)

Ao subtrair todos os valores ( a - b onde a> b ) usando uma etapa de 0,1 (de 100 a 0,1), temos ~ 34% de chance de erro de precisão . aqui estão alguns exemplos:

0.6 - 0.2 = 0.39999999999999997 (SMALLER)
0.5 - 0.4 = 0.09999999999999998 (SMALLER)
...
2.1 - 0.2 = 1.9000000000000001 (BIGGER)
2.0 - 1.9 = 0.10000000000000009 (BIGGER)
...
100 - 99.9 = 0.09999999999999432 (SMALLER)
100 - 99.8 = 0.20000000000000284 (BIGGER)

* 15% e 34% são realmente enormes, então sempre use BigDecimal quando a precisão for muito importante. Com 2 dígitos decimais (passo 0,01) a situação piora um pouco mais (18% e 36%).

Answer 13

Não, não quebrado, mas a maioria das frações decimais deve ser aproximada

Resumo

A aritmética de vírgula flutuante é exata, infelizmente, não combina bem com nossa representação de número de base 10 usual, então acontece que muitas vezes fornecemos uma entrada um pouco diferente do que escrevemos.

Mesmo números simples como 0,01, 0,02, 0,03, 0,04 ... 0,24 não são representáveis ​​exatamente como frações binárias. Se você contar 0,01, 0,02, 0,03 ..., só depois de chegar a 0,25 você obterá a primeira fração representável na base ₂ . Se você tentasse isso usando FP, seu 0,01 ficaria ligeiramente errado, então a única maneira de adicionar 25 deles até um bom 0,25 exato teria exigido uma longa cadeia de causalidade envolvendo bits de guarda e arredondamento. É difícil prever, então levantamos nossas mãos e dizemos "FP é inexato", mas isso não é verdade.

Constantemente damos ao hardware FP algo que parece simples na base 10, mas é uma fração repetida na base 2.

Como isso aconteceu?

Quando escrevemos em decimal, cada fração (especificamente, cada decimal final) é um número racional da forma

           a / (2 ⁿ x 5 ^m )

Em binário, obtemos apenas o termo 2 ⁿ , ou seja:

           a / 2 ⁿ

Assim, em decimal, não podemos representar ¹ / ₃ . Como a base 10 inclui 2 como fator primo, cada número que podemos escrever como uma fração binária também pode ser escrito como uma fração de base 10. No entanto, quase nada que escrevemos como uma fração de base ₁₀ é representável em binário. No intervalo de 0,01, 0,02, 0,03 ... 0,99, apenas três números podem ser representados em nosso formato FP: 0,25, 0,50 e 0,75, porque eles são 1/4, 1/2 e 3/4, todos números com um fator primo usando apenas o termo 2 ⁿ .

Na base de ₁₀ nós não pode representar ¹ / ₃ . Mas em binário, não podemos fazer ¹ / ₁₀ ou ¹ / ₃ .

Portanto, embora cada fração binária possa ser escrita em decimal, o inverso não é verdadeiro. E, de fato, a maioria das frações decimais se repetem em binário.

Lidando com isso

Os desenvolvedores geralmente são instruídos a fazer comparações <epsilon , o melhor conselho pode ser arredondar para valores integrais (na biblioteca C: round () e roundf (), ou seja, permanecer no formato FP) e depois comparar. O arredondamento para um comprimento de fração decimal específico resolve a maioria dos problemas de saída.

Além disso, em problemas de processamento de números reais (os problemas para os quais o FP foi inventado nos primeiros computadores terrivelmente caros), as constantes físicas do universo e todas as outras medições são conhecidas apenas por um número relativamente pequeno de algarismos significativos, portanto, todo o espaço do problema era "inexato" de qualquer maneira. A "precisão" do FP não é um problema neste tipo de aplicação.

Toda a questão realmente surge quando as pessoas tentam usar FP para contagem de grãos. Funciona para isso, mas apenas se você se limitar a valores integrais, o que meio que frustra o sentido de usá-lo. É por isso que temos todas aquelas bibliotecas de software de fração decimal.

Adoro a resposta Pizza de Chris , porque descreve o problema real, não apenas o aceno de mão usual sobre "imprecisão". Se o FP fosse simplesmente "impreciso", poderíamos consertar isso e teríamos feito isso décadas atrás. A razão de não termos feito isso é porque o formato FP é compacto e rápido e é a melhor maneira de processar muitos números. Além disso, é um legado da era espacial e da corrida armamentista e das primeiras tentativas de resolver grandes problemas com computadores muito lentos usando pequenos sistemas de memória. (Às vezes, núcleos magnéticos individuais para armazenamento de 1 bit, mas isso é outra história. )

Conclusion

If you are just counting beans at a bank, software solutions that use decimal string representations in the first place work perfectly well. But you can't do quantum chromodynamics or aerodynamics that way.

Answer 14

In short it's because:

Floating point numbers cannot represent all decimals precisely in binary

So just like 3/10 which does not exist in base 10 precisely (it will be 3.33... recurring), in the same way 1/10 doesn't exist in binary.

So what? How to deal with it? Is there any workaround?

In order to offer The best solution I can say I discovered following method:

parseFloat((0.1 + 0.2).toFixed(10)) => Will return 0.3

Let me explain why it's the best solution. As others mentioned in above answers it's a good idea to use ready to use Javascript toFixed() function to solve the problem. But most likely you'll encounter with some problems.

Imagine you are going to add up two float numbers like 0.2 and 0.7 here it is: 0.2 + 0.7 = 0.8999999999999999.

Your expected result was 0.9 it means you need a result with 1 digit precision in this case. So you should have used (0.2 + 0.7).tofixed(1) but you can't just give a certain parameter to toFixed() since it depends on the given number, for instance

0.22 + 0.7 = 0.9199999999999999

In this example you need 2 digits precision so it should be toFixed(2), so what should be the paramter to fit every given float number?

You might say let it be 10 in every situation then:

(0.2 + 0.7).toFixed(10) => Result will be "0.9000000000"

Damn! What are you going to do with those unwanted zeros after 9? It's the time to convert it to float to make it as you desire:

parseFloat((0.2 + 0.7).toFixed(10)) => Result will be 0.9

Now that you found the solution, it's better to offer it as a function like this:

function floatify(number){
           return parseFloat((number).toFixed(10));
        }
    

Let's try it yourself:

function floatify(number){
       return parseFloat((number).toFixed(10));
    }
 
function addUp(){
  var number1 = +$("#number1").val(); var number2 = +$("#number2").val();
  var unexpectedResult = number1 + number2;
  var expectedResult = floatify(number1 + number2);
  $("#unexpectedResult").text(unexpectedResult); $("#expectedResult").text(expectedResult);
}
addUp();

input{
  width: 50px;
}
#expectedResult{
color: green;
}
#unexpectedResult{
color: red;
}

<script src="https://ajax.googleapis.com/ajax/libs/jquery/2.1.1/jquery.min.js"></script>
<input id="number1" value="0.2" onclick="addUp()" onkeyup="addUp()"/> +
<input id="number2" value="0.7" onclick="addUp()" onkeyup="addUp()"/> =
<p>Expected Result: <span id="expectedResult"></span></p>
<p>Unexpected Result: <span id="unexpectedResult"></span></p>

You can use it this way:

var x = 0.2 + 0.7;
floatify(x);  => Result: 0.9

As W3SCHOOLS suggests there is another solution too, you can multiply and divide to solve the problem above:

var x = (0.2 * 10 + 0.1 * 10) / 10;       // x will be 0.3

Keep in mind that (0.2 + 0.1) * 10 / 10 won't work at all although it seems the same! I prefer the first solution since I can apply it as a function which converts the input float to accurate output float.

Answer 15

Did you try the duct tape solution?

Try to determine when errors occur and fix them with short if statements, it's not pretty but for some problems it is the only solution and this is one of them.

 if( (n * 0.1) < 100.0 ) { return n * 0.1 - 0.000000000000001 ;}
                    else { return n * 0.1 + 0.000000000000001 ;}    

I had the same problem in a scientific simulation project in c#, and I can tell you that if you ignore the butterfly effect it's gonna turn to a big fat dragon and bite you in the a**

Answer 16

Those weird numbers appear because computers use binary(base 2) number system for calculation purposes, while we use decimal(base 10).

There are a majority of fractional numbers that cannot be represented precisely either in binary or in decimal or both. Result - A rounded up (but precise) number results.

Answer 17

Given that nobody has mentioned this...

Some high level languages such as Python and Java come with tools to overcome binary floating point limitations. For example:

• Python's decimal module and Java's BigDecimal class, that represent numbers internally with decimal notation (as opposed to binary notation). Both have limited precision, so they are still error prone, however they solve most common problems with binary floating point arithmetic.

  Decimals are very nice when dealing with money: ten cents plus twenty cents are always exactly thirty cents:

  >>> 0.1 + 0.2 == 0.3
  False
  >>> Decimal('0.1') + Decimal('0.2') == Decimal('0.3')
  True
  

  Python's decimal module is based on IEEE standard 854-1987.

• Python's fractions module and Apache Common's BigFraction class. Both represent rational numbers as (numerator, denominator) pairs and they may give more accurate results than decimal floating point arithmetic.

Neither of these solutions is perfect (especially if we look at performances, or if we require a very high precision), but still they solve a great number of problems with binary floating point arithmetic.

Answer 18

Many of this question's numerous duplicates ask about the effects of floating point rounding on specific numbers. In practice, it is easier to get a feeling for how it works by looking at exact results of calculations of interest rather than by just reading about it. Some languages provide ways of doing that - such as converting a float or double to BigDecimal in Java.

Since this is a language-agnostic question, it needs language-agnostic tools, such as a Decimal to Floating-Point Converter.

Applying it to the numbers in the question, treated as doubles:

0.1 converts to 0.1000000000000000055511151231257827021181583404541015625,

0.2 converts to 0.200000000000000011102230246251565404236316680908203125,

0.3 converts to 0.299999999999999988897769753748434595763683319091796875, and

0.30000000000000004 converts to 0.3000000000000000444089209850062616169452667236328125.

Adding the first two numbers manually or in a decimal calculator such as Full Precision Calculator, shows the exact sum of the actual inputs is 0.3000000000000000166533453693773481063544750213623046875.

If it were rounded down to the equivalent of 0.3 the rounding error would be 0.0000000000000000277555756156289135105907917022705078125. Rounding up to the equivalent of 0.30000000000000004 also gives rounding error 0.0000000000000000277555756156289135105907917022705078125. The round-to-even tie breaker applies.

Returning to the floating point converter, the raw hexadecimal for 0.30000000000000004 is 3fd3333333333334, which ends in an even digit and therefore is the correct result.

Answer 19

Can I just add; people always assume this to be a computer problem, but if you count with your hands (base 10), you can't get (1/3+1/3=2/3)=true unless you have infinity to add 0.333... to 0.333... so just as with the (1/10+2/10)!==3/10 problem in base 2, you truncate it to 0.333 + 0.333 = 0.666 and probably round it to 0.667 which would be also be technically inaccurate.

Count in ternary, and thirds are not a problem though - maybe some race with 15 fingers on each hand would ask why your decimal math was broken...

Answer 20

The kind of floating-point math that can be implemented in a digital computer necessarily uses an approximation of the real numbers and operations on them. (The standard version runs to over fifty pages of documentation and has a committee to deal with its errata and further refinement.)

This approximation is a mixture of approximations of different kinds, each of which can either be ignored or carefully accounted for due to its specific manner of deviation from exactitude. It also involves a number of explicit exceptional cases at both the hardware and software levels that most people walk right past while pretending not to notice.

If you need infinite precision (using the number π, for example, instead of one of its many shorter stand-ins), you should write or use a symbolic math program instead.

But if you're okay with the idea that sometimes floating-point math is fuzzy in value and logic and errors can accumulate quickly, and you can write your requirements and tests to allow for that, then your code can frequently get by with what's in your FPU.

Answer 21

Just for fun, I played with the representation of floats, following the definitions from the Standard C99 and I wrote the code below.

The code prints the binary representation of floats in 3 separated groups

SIGN EXPONENT FRACTION

and after that it prints a sum, that, when summed with enough precision, it will show the value that really exists in hardware.

So when you write float x = 999..., the compiler will transform that number in a bit representation printed by the function xx such that the sum printed by the function yy be equal to the given number.

In reality, this sum is only an approximation. For the number 999,999,999 the compiler will insert in bit representation of the float the number 1,000,000,000

After the code I attach a console session, in which I compute the sum of terms for both constants (minus PI and 999999999) that really exists in hardware, inserted there by the compiler.

#include <stdio.h>
#include <limits.h>

void
xx(float *x)
{
    unsigned char i = sizeof(*x)*CHAR_BIT-1;
    do {
        switch (i) {
        case 31:
             printf("sign:");
             break;
        case 30:
             printf("exponent:");
             break;
        case 23:
             printf("fraction:");
             break;

        }
        char b=(*(unsigned long long*)x&((unsigned long long)1<<i))!=0;
        printf("%d ", b);
    } while (i--);
    printf("\n");
}

void
yy(float a)
{
    int sign=!(*(unsigned long long*)&a&((unsigned long long)1<<31));
    int fraction = ((1<<23)-1)&(*(int*)&a);
    int exponent = (255&((*(int*)&a)>>23))-127;

    printf(sign?"positive" " ( 1+":"negative" " ( 1+");
    unsigned int i = 1<<22;
    unsigned int j = 1;
    do {
        char b=(fraction&i)!=0;
        b&&(printf("1/(%d) %c", 1<<j, (fraction&(i-1))?'+':')' ), 0);
    } while (j++, i>>=1);

    printf("*2^%d", exponent);
    printf("\n");
}

void
main()
{
    float x=-3.14;
    float y=999999999;
    printf("%lu\n", sizeof(x));
    xx(&x);
    xx(&y);
    yy(x);
    yy(y);
}

---

Here is a console session in which I compute the real value of the float that exists in hardware. I used bc to print the sum of terms outputted by the main program. One can insert that sum in python repl or something similar also.

-- .../terra1/stub
@ qemacs f.c
-- .../terra1/stub
@ gcc f.c
-- .../terra1/stub
@ ./a.out
sign:1 exponent:1 0 0 0 0 0 0 fraction:0 1 0 0 1 0 0 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 1
sign:0 exponent:1 0 0 1 1 1 0 fraction:0 1 1 0 1 1 1 0 0 1 1 0 1 0 1 1 0 0 1 0 1 0 0 0
negative ( 1+1/(2) +1/(16) +1/(256) +1/(512) +1/(1024) +1/(2048) +1/(8192) +1/(32768) +1/(65536) +1/(131072) +1/(4194304) +1/(8388608) )*2^1
positive ( 1+1/(2) +1/(4) +1/(16) +1/(32) +1/(64) +1/(512) +1/(1024) +1/(4096) +1/(16384) +1/(32768) +1/(262144) +1/(1048576) )*2^29
-- .../terra1/stub
@ bc
scale=15
( 1+1/(2) +1/(4) +1/(16) +1/(32) +1/(64) +1/(512) +1/(1024) +1/(4096) +1/(16384) +1/(32768) +1/(262144) +1/(1048576) )*2^29
999999999.999999446351872

That's it. The value of 999999999 is in fact

999999999.999999446351872

You can also check with bc that -3.14 is also perturbed. Do not forget to set a scale factor in bc.

The displayed sum is what inside the hardware. The value you obtain by computing it depends on the scale you set. I did set the scale factor to 15. Mathematically, with infinite precision, it seems it is 1,000,000,000.

Answer 22

Another way to look at this: Used are 64 bits to represent numbers. As consequence there is no way more than 2**64 = 18,446,744,073,709,551,616 different numbers can be precisely represented.

However, Math says there are already infinitely many decimals between 0 and 1. IEE 754 defines an encoding to use these 64 bits efficiently for a much larger number space plus NaN and +/- Infinity, so there are gaps between accurately represented numbers filled with numbers only approximated.

Unfortunately 0.3 sits in a gap.

Answer 23

Since Python 3.5 you can use math.isclose() function for testing approximate equality:

>>> import math
>>> math.isclose(0.1 + 0.2, 0.3)
True
>>> 0.1 + 0.2 == 0.3
False

Answer 24

Imagine working in base ten with, say, 8 digits of accuracy. You check whether

1/3 + 2 / 3 == 1

and learn that this returns false. Why? Well, as real numbers we have

1/3 = 0.333.... and 2/3 = 0.666....

Truncating at eight decimal places, we get

0.33333333 + 0.66666666 = 0.99999999

which is, of course, different from 1.00000000 by exactly 0.00000001.

---

The situation for binary numbers with a fixed number of bits is exactly analogous. As real numbers, we have

1/10 = 0.0001100110011001100... (base 2)

and

1/5 = 0.0011001100110011001... (base 2)

If we truncated these to, say, seven bits, then we'd get

0.0001100 + 0.0011001 = 0.0100101

while on the other hand,

3/10 = 0.01001100110011... (base 2)

which, truncated to seven bits, is 0.0100110, and these differ by exactly 0.0000001.

---

The exact situation is slightly more subtle because these numbers are typically stored in scientific notation. So, for instance, instead of storing 1/10 as 0.0001100 we may store it as something like 1.10011 * 2^-4, depending on how many bits we've allocated for the exponent and the mantissa. This affects how many digits of precision you get for your calculations.

The upshot is that because of these rounding errors you essentially never want to use == on floating-point numbers. Instead, you can check if the absolute value of their difference is smaller than some fixed small number.

Answer 25

Decimal numbers such as 0.1, 0.2, and 0.3 are not represented exactly in binary encoded floating point types. The sum of the approximations for 0.1 and 0.2 differs from the approximation used for 0.3, hence the falsehood of 0.1 + 0.2 == 0.3 as can be seen more clearly here:

#include <stdio.h>

int main() {
    printf("0.1 + 0.2 == 0.3 is %s\n", 0.1 + 0.2 == 0.3 ? "true" : "false");
    printf("0.1 is %.23f\n", 0.1);
    printf("0.2 is %.23f\n", 0.2);
    printf("0.1 + 0.2 is %.23f\n", 0.1 + 0.2);
    printf("0.3 is %.23f\n", 0.3);
    printf("0.3 - (0.1 + 0.2) is %g\n", 0.3 - (0.1 + 0.2));
    return 0;
}

Output:

0.1 + 0.2 == 0.3 is false
0.1 is 0.10000000000000000555112
0.2 is 0.20000000000000001110223
0.1 + 0.2 is 0.30000000000000004440892
0.3 is 0.29999999999999998889777
0.3 - (0.1 + 0.2) is -5.55112e-17

For these computations to be evaluated more reliably, you would need to use a decimal-based representation for floating point values. The C Standard does not specify such types by default but as an extension described in a technical Report.

The _Decimal32, _Decimal64 and _Decimal128 types might be available on your system (for example, GCC supports them on selected targets, but Clang does not support them on OS X).

Answer 26

Since this thread branched off a bit into a general discussion over current floating point implementations I'd add that there are projects on fixing their issues.

Take a look at https://posithub.org/ for example, which showcases a number type called posit (and its predecessor unum) that promises to offer better accuracy with fewer bits. If my understanding is correct, it also fixes the kind of problems in the question. Quite interesting project, the person behind it is a mathematician it Dr. John Gustafson. The whole thing is open source, with many actual implementations in C/C++, Python, Julia and C# (https://hastlayer.com/arithmetics).

Answer 27

It's actually pretty simple. When you have a base 10 system (like ours), it can only express fractions that use a prime factor of the base. The prime factors of 10 are 2 and 5. So 1/2, 1/4, 1/5, 1/8, and 1/10 can all be expressed cleanly because the denominators all use prime factors of 10. In contrast, 1/3, 1/6, and 1/7 are all repeating decimals because their denominators use a prime factor of 3 or 7. In binary (or base 2), the only prime factor is 2. So you can only express fractions cleanly which only contain 2 as a prime factor. In binary, 1/2, 1/4, 1/8 would all be expressed cleanly as decimals. While, 1/5 or 1/10 would be repeating decimals. So 0.1 and 0.2 (1/10 and 1/5) while clean decimals in a base 10 system, are repeating decimals in the base 2 system the computer is operating in. When you do math on these repeating decimals, you end up with leftovers which carry over when you convert the computer's base 2 (binary) number into a more human readable base 10 number.

From https://0.30000000000000004.com/

Answer 28

Normal arithmetic is base-10, so decimals represent tenths, hundredths, etc. When you try to represent a floating-point number in binary base-2 arithmetic, you are dealing with halves, fourths, eighths, etc.

In the hardware, floating points are stored as integer mantissas and exponents. Mantissa represents the significant digits. Exponent is like scientific notation but it uses a base of 2 instead of 10. For example 64.0 would be represented with a mantissa of 1 and exponent of 6. 0.125 would be represented with a mantissa of 1 and an exponent of -3.

Floating point decimals have to add up negative powers of 2

0.1b = 0.5d
0.01b = 0.25d
0.001b = 0.125d
0.0001b = 0.0625d
0.00001b = 0.03125d

and so on.

It is common to use a error delta instead of using equality operators when dealing with floating point arithmetic. Instead of

if(a==b) ...

you would use

delta = 0.0001; // or some arbitrarily small amount
if(a - b > -delta && a - b < delta) ...

Answer 29

Floating point numbers are represented, at the hardware level, as fractions of binary numbers (base 2). For example, the decimal fraction:

0.125

has the value 1/10 + 2/100 + 5/1000 and, in the same way, the binary fraction:

0.001

has the value 0/2 + 0/4 + 1/8. These two fractions have the same value, the only difference is that the first is a decimal fraction, the second is a binary fraction.

Unfortunately, most decimal fractions cannot have exact representation in binary fractions. Therefore, in general, the floating point numbers you give are only approximated to binary fractions to be stored in the machine.

The problem is easier to approach in base 10. Take for example, the fraction 1/3. You can approximate it to a decimal fraction:

0.3

or better,

0.33

or better,

0.333

etc. No matter how many decimal places you write, the result is never exactly 1/3, but it is an estimate that always comes closer.

Likewise, no matter how many base 2 decimal places you use, the decimal value 0.1 cannot be represented exactly as a binary fraction. In base 2, 1/10 is the following periodic number:

0.0001100110011001100110011001100110011001100110011 ...

Stop at any finite amount of bits, and you'll get an approximation.

For Python, on a typical machine, 53 bits are used for the precision of a float, so the value stored when you enter the decimal 0.1 is the binary fraction.

0.00011001100110011001100110011001100110011001100110011010

which is close, but not exactly equal, to 1/10.

It's easy to forget that the stored value is an approximation of the original decimal fraction, due to the way floats are displayed in the interpreter. Python only displays a decimal approximation of the value stored in binary. If Python were to output the true decimal value of the binary approximation stored for 0.1, it would output:

>>> 0.1
0.1000000000000000055511151231257827021181583404541015625

This is a lot more decimal places than most people would expect, so Python displays a rounded value to improve readability:

>>> 0.1
0.1

It is important to understand that in reality this is an illusion: the stored value is not exactly 1/10, it is simply on the display that the stored value is rounded. This becomes evident as soon as you perform arithmetic operations with these values:

>>> 0.1 + 0.2
0.30000000000000004

This behavior is inherent to the very nature of the machine's floating-point representation: it is not a bug in Python, nor is it a bug in your code. You can observe the same type of behavior in all other languages ​​that use hardware support for calculating floating point numbers (although some languages ​​do not make the difference visible by default, or not in all display modes).

Another surprise is inherent in this one. For example, if you try to round the value 2.675 to two decimal places, you will get

>>> round (2.675, 2)
2.67

The documentation for the round() primitive indicates that it rounds to the nearest value away from zero. Since the decimal fraction is exactly halfway between 2.67 and 2.68, you should expect to get (a binary approximation of) 2.68. This is not the case, however, because when the decimal fraction 2.675 is converted to a float, it is stored by an approximation whose exact value is :

2.67499999999999982236431605997495353221893310546875

Since the approximation is slightly closer to 2.67 than 2.68, the rounding is down.

If you are in a situation where rounding decimal numbers halfway down matters, you should use the decimal module. By the way, the decimal module also provides a convenient way to "see" the exact value stored for any float.

>>> from decimal import Decimal
>>> Decimal (2.675)
>>> Decimal ('2.67499999999999982236431605997495353221893310546875')

Another consequence of the fact that 0.1 is not exactly stored in 1/10 is that the sum of ten values ​​of 0.1 does not give 1.0 either:

>>> sum = 0.0
>>> for i in range (10):
... sum + = 0.1
...>>> sum
0.9999999999999999

The arithmetic of binary floating point numbers holds many such surprises. The problem with "0.1" is explained in detail below, in the section "Representation errors". See The Perils of Floating Point for a more complete list of such surprises.

It is true that there is no simple answer, however do not be overly suspicious of floating virtula numbers! Errors, in Python, in floating-point number operations are due to the underlying hardware, and on most machines are no more than 1 in 2 ** 53 per operation. This is more than necessary for most tasks, but you should keep in mind that these are not decimal operations, and every operation on floating point numbers may suffer from a new error.

Although pathological cases exist, for most common use cases you will get the expected result at the end by simply rounding up to the number of decimal places you want on the display. For fine control over how floats are displayed, see String Formatting Syntax for the formatting specifications of the str.format () method.

This part of the answer explains in detail the example of "0.1" and shows how you can perform an exact analysis of this type of case on your own. We assume that you are familiar with the binary representation of floating point numbers.The term Representation error means that most decimal fractions cannot be represented exactly in binary. This is the main reason why Python (or Perl, C, C ++, Java, Fortran, and many others) usually doesn't display the exact result in decimal:

>>> 0.1 + 0.2
0.30000000000000004

Why ? 1/10 and 2/10 are not representable exactly in binary fractions. However, all machines today (July 2010) follow the IEEE-754 standard for the arithmetic of floating point numbers. and most platforms use an "IEEE-754 double precision" to represent Python floats. Double precision IEEE-754 uses 53 bits of precision, so on reading the computer tries to convert 0.1 to the nearest fraction of the form J / 2 ** N with J an integer of exactly 53 bits. Rewrite :

1/10 ~ = J / (2 ** N)

in :

J ~ = 2 ** N / 10

remembering that J is exactly 53 bits (so> = 2 ** 52 but <2 ** 53), the best possible value for N is 56:

>>> 2 ** 52
4503599627370496
>>> 2 ** 53
9007199254740992
>>> 2 ** 56/10
7205759403792793

So 56 is the only possible value for N which leaves exactly 53 bits for J. The best possible value for J is therefore this quotient, rounded:

>>> q, r = divmod (2 ** 56, 10)
>>> r
6

Since the carry is greater than half of 10, the best approximation is obtained by rounding up:

>>> q + 1
7205759403792794

Therefore the best possible approximation for 1/10 in "IEEE-754 double precision" is this above 2 ** 56, that is:

7205759403792794/72057594037927936

Note that since the rounding was done upward, the result is actually slightly greater than 1/10; if we hadn't rounded up, the quotient would have been slightly less than 1/10. But in no case is it exactly 1/10!

So the computer never "sees" 1/10: what it sees is the exact fraction given above, the best approximation using the double precision floating point numbers from the "" IEEE-754 ":

>>>. 1 * 2 ** 56
7205759403792794.0

If we multiply this fraction by 10 ** 30, we can observe the values ​​of its 30 decimal places of strong weight.

>>> 7205759403792794 * 10 ** 30 // 2 ** 56
100000000000000005551115123125L

meaning that the exact value stored in the computer is approximately equal to the decimal value 0.100000000000000005551115123125. In versions prior to Python 2.7 and Python 3.1, Python rounded these values ​​to 17 significant decimal places, displaying “0.10000000000000001”. In current versions of Python, the displayed value is the value whose fraction is as short as possible while giving exactly the same representation when converted back to binary, simply displaying “0.1”.

Answer 30

I just saw this interesting issue around floating points:

Consider the following results:

error = (2**53+1) - int(float(2**53+1))

>>> (2**53+1) - int(float(2**53+1))
1

We can clearly see a breakpoint when 2**53+1 - all works fine until 2**53.

>>> (2**53) - int(float(2**53))
0

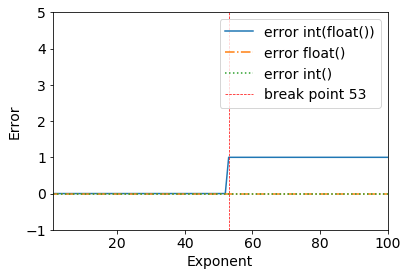
This happens because of the double-precision binary: IEEE 754 double-precision binary floating-point format: binary64

From the Wikipedia page for Double-precision floating-point format:

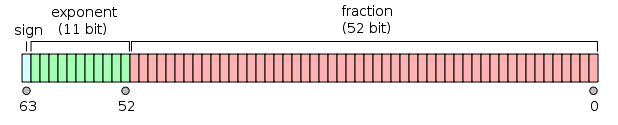
Double-precision binary floating-point is a commonly used format on PCs, due to its wider range over single-precision floating point, in spite of its performance and bandwidth cost. As with single-precision floating-point format, it lacks precision on integer numbers when compared with an integer format of the same size. It is commonly known simply as double. The IEEE 754 standard specifies a binary64 as having:

• Sign bit: 1 bit
• Exponent: 11 bits
• Significant precision: 53 bits (52 explicitly stored)

The real value assumed by a given 64-bit double-precision datum with a given biased exponent and a 52-bit fraction is

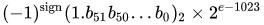
or

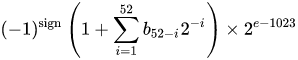
Thanks to @a_guest for pointing that out to me.