Qual seria o tamanho de um código QR no meu telhado para que um satélite pudesse digitalizá-lo com a resolução permitida de hoje?

Jan 26 2021

Digamos, usando os satélites Planet Labs

Obrigada

Respostas

7 uhoh Jan 28 2021 at 04:55

Qual seria o tamanho de um código QR no meu telhado para que um satélite pudesse digitalizá-lo com a resolução permitida de hoje?

Digamos, usando os satélites Planet Labs

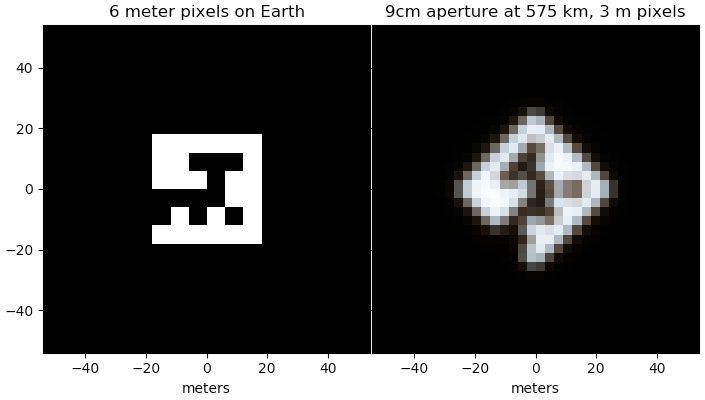
Esta é uma resposta complementar. Eu simulei pixels "QR" de 6 metros vistos do espaço com uma abertura de 9 cm (no final de um cubo Dove 3U) em comprimentos de onda de 450, 550 e 650 nm, girados em 45 graus e, em seguida, amostrados com pixels de 3 metros.

É um script fragmentado e frágil, mas faz o trabalho.

A imagem apóia a conclusão principal na outra resposta de que este é provavelmente o tamanho mínimo para alguma confiabilidade de vê-lo com um Dove.

O script está abaixo do ideal, fui preguiçoso e usei PIL para girar, poderia ter interpolado scipy.ndimage.map_coordinatese poderia ter "difundido" em scipy.ndimage.gaussian_filtervez de um disco Airy sofisticado.

Os matizes na imagem final são devidos aos limites de difração dependentes do comprimento de onda da abertura, a aproximadamente $1.22 \lambda / D$ variação da resolução angular com relação entre comprimento de onda e abertura.

import numpy as np
import matplotlib.pyplot as plt
import itertools
from PIL import Image
from scipy import special as spe
from scipy.ndimage import convolve

N = 5*2

data = ('111111' + '110001' + '111011' +
        '000011' + '010101' + '111111')
data = np.array([int(x) for x in data]).reshape((6, 6))
data = np.pad(data, ((6, 6), (6, 6)))

img = np.zeros((N*18, N*18, 3))

for i, j in itertools.product(np.arange(18), repeat=2):
    img[N*i:N*(i+1), N*j:N*(j+1)] = data[i, j]

pixsize = 6 # meters
scale = pixsize/N
extent = 9*N * scale * np.array([-1, 1, -1, 1])

R = 575 * 1000. # meters distance
x = 4*N * scale * np.linspace(-1, 1, 8*N)
X, Y = np.meshgrid(x, x)
q = np.sqrt(X**2 + Y**2)
wavelengths = 1E-09 * np.array([650, 550, 450])

a = 0.045 # radius of aperture in meters (looking out end of a 3U cubesat)
x = (2 * np.pi * a / wavelengths) * (q[..., None] / R)

# https://en.wikipedia.org/wiki/Airy_disk
airy = (2 * spe.j1(x) / x)**2
areas = airy.sum(axis=0).sum(axis=0)
airy /= areas

new = [convolve(img[..., i], airy[..., i]) for i in range(3)]
newarray = np.stack(new, axis=2)
newarray = np.uint8(255 * newarray/newarray.max())

newimg = Image.fromarray(newarray)
newimg45 = newimg.rotate(45)
newimg45.show()
n45 = np.array(list(newimg45.getdata())).reshape(18*2, N>>1, 18*2, N>>1, 3)
n45 = np.uint8(n45.sum(axis=(1, 3)) / (N>>1)**2)

if True:
    plt.figure()
    plt.subplot(1, 2, 1)
    plt.imshow(img, extent=extent)
    plt.title('6 meter pixels on Earth')
    plt.xlabel('meters')
    plt.subplot(1, 2, 2)
    plt.imshow(n45, extent=extent)
    plt.title('9cm aperture at 575 km, 3 m pixels')
    plt.xlabel('meters')
    plt.show()

4 uhoh Jan 27 2021 at 08:30

Qual seria o tamanho de um código QR no meu telhado para que um satélite pudesse digitalizá-lo com a resolução permitida de hoje?

Digamos, usando os satélites Planet Labs

tl; dr: usando 6x6 " tag de realidade aumentada " discutida na resposta de @CamilleGoudeseune como a do rover Curiosity e pixels de 6 metros (duas resoluções mínimas para permitir translação e rotação arbitrárias), seu padrão deve ser 36 x 36 metros para ter um boa mudança de ser visto e recuperado de uma imagem de um PlanetLabs Dove.

Eu removeria a refletividade vermelha e infravermelha das áreas brilhantes e codificaria apenas nos comprimentos de onda mais curtos, uma vez que as pombas têm quatro canais de cor são (provavelmente) limitados por difração e comprimentos de onda mais longos podem ter pior resolução.

Tente excitar apenas as bandas de comprimento de onda mais curtas de sua espaçonave para torná-las "pop-out" para observadores casuais, ou apenas olhe para esses comprimentos de onda no produto de dados final se estiver procurando por si mesmo.

No https://www.planet.com/products/planet-imagery/os mais numerosos satélites ou "pombas" fornecem dados para o produto de dados PLANETSCOPE. Diz-se que os satélites têm resolução de 3,7 metros e o produto de dados tem um tamanho de pixel reamostrado de 3 metros. Veja também a resposta de @djr para Are these images from Planet Labs? As imagens estão publicamente disponíveis?

Se você tivesse muita sorte de ter os pixels alinhados com seu padrão QR tanto translacional quanto rotacionalmente, eles poderiam teoricamente ter 3 metros.

No entanto, na prática, dada a translação e rotação arbitrárias de seu padrão dentro do campo da imagem, você deve tê-los um fator de pelo menos 2, se não 3 maior do que isso.

@Uwe nos lembra que um pequeno código QR ainda seria muito grande. Existem códigos QR 11 x 11 Micro e os astronautas têm usado números de pixels ainda menores como alternativas aos códigos QR com ainda menos pixels.