Статистика - Центральная предельная теорема

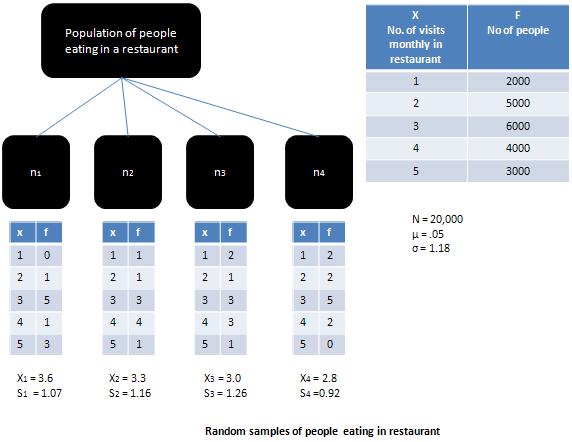
Если совокупность, из которой была взята выборка, является нормальной совокупностью, тогда sample means будет равно среднему значению по совокупности, а sampling distributionбыло бы нормально. Когда большая часть населения искажена, как показано на рисунке, тогдаsampling distribution будет иметь тенденцию приближаться к нормальному распределению при условии, что выборка велика (то есть больше 30).

В соответствии с Central Limit Theorem, для достаточно больших образцов размером более 30 форма sampling distribution будет все больше и больше походить на normal distribution, независимо от формы родительского населения. Эта теорема объясняет связь междуpopulation distribution и sampling distribution. Это подчеркивает тот факт, что если имеется достаточно большой набор образцов, тоsampling distribution средних подходов normal distribution. Важность центральной предельной теоремы была резюмирована Ричардом. И. Левина в следующих словах:

Значение центральной предельной теоремы заключается в том, что она позволяет нам использовать статистику выборки, чтобы делать выводы о параметрах совокупности, не зная ничего о форме частотного распределения этой совокупности, кроме того, что мы можем получить из выборки.