Статистика - распределение хи-квадрат

Распределение хи-квадрат (хи-квадрат или $ {X ^ 2} $ - распределение) со степенями свободы, k - это распределение суммы квадратов k независимых стандартных нормальных случайных величин. Это одно из наиболее широко используемых распределений вероятностей в статистике. Это частный случай гамма-распределения.

Распределение хи-квадрат широко используется статистиками для вычисления следующего:

Оценка доверительного интервала для стандартного отклонения совокупности нормального распределения с использованием стандартного отклонения выборки.
Проверить независимость двух критериев классификации множества качественных переменных.
Чтобы проверить отношения между категориальными переменными.
Для изучения дисперсии выборки, в которой основное распределение является нормальным.
Проверить отклонения разницы между ожидаемой и наблюдаемой частотами.
Провести тест хи-квадрат (критерий согласия).

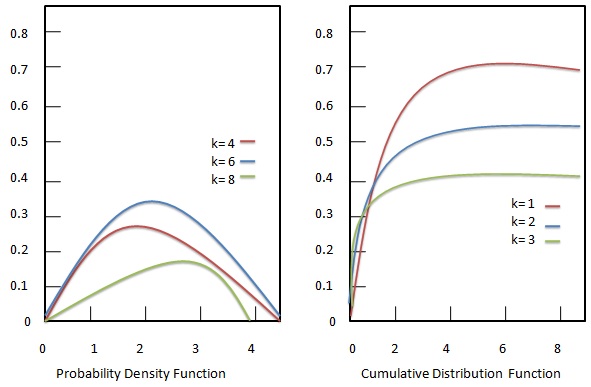
Функция плотности вероятности

Функция плотности вероятности распределения хи-квадрат определяется как:

Формула

$ {f (x; k) =} $ $ \ begin {cases} \ frac {x ^ {\ frac {k} {2} - 1} e ^ {- \ frac {x} {2}}} {2 ^ {\ frac {k} {2}} \ Gamma (\ frac {k} {2})}, & \ text {if $ x \ gt 0 $} \\ [7pt] 0, & \ text {if $ x \ le 0 $} \ end {case} $

Где -

$ {\ Gamma (\ frac {k} {2})} $ = Гамма-функция, имеющая значения в замкнутой форме для целочисленного параметра k.
$ {x} $ = случайная величина.
$ {k} $ = целочисленный параметр.