Статистика - эксцесс

Степень хвостичности распределения измеряется эксцессом. Он говорит нам, в какой степени распределение более или менее подвержено выбросам (более тяжелым или легким хвостом), чем нормальное распределение. Три разных типа кривых, любезно предоставленные Investopedia, показаны следующим образом:

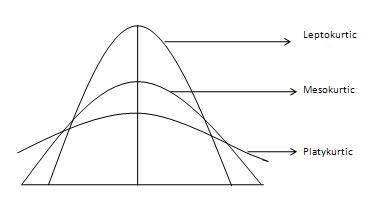
На графиках плотности (левая панель) трудно различить различные типы эксцесса, потому что хвосты близки к нулю для всех распределений. Но различия в хвостах легко увидеть на обычных графиках квантиль-квантиль (правая панель).

Нормальная кривая называется мезокуртической кривой. Если кривая распределения более склонна к выбросам (или имеет более тяжелый хвост), чем нормальная или мезокуртическая кривая, то ее называют лептокуртической кривой. Если кривая менее склонна к выбросам (или имеет более легкий хвост), чем нормальная кривая, она называется платикуртической кривой. Эксцесс измеряется моментами и определяется по следующей формуле -

Формула

$ {\ beta_2 = \ frac {\ mu_4} {\ mu_2}} $

Где -

$ {\ mu_4 = \ frac {\ sum (x- \ bar x) ^ 4} {N}} $

Чем больше значение \ beta_2, тем больше пик или лептокуртичность кривой. Нормальная кривая имеет значение 3, лептокуртика имеет значение \ beta_2 больше 3, а пластиковая кривая имеет значение \ beta_2 меньше 3.

пример

Problem Statement:

Приведены данные о дневной заработной плате 45 рабочих завода. Вычислите \ beta_1 и \ beta_2, используя момент относительно среднего. Прокомментируйте результаты.

Заработная плата (рупии)	Количество рабочих
100-200	1
120-200	2
140-200	6
160-200	20
180-200	11
200-200	3
220-200	2

Solution:

Заработная плата (рупии)	Количество рабочих (ж)	Средняя точка м	m - $ {\ frac {170} {20}} $ d	$ {fd} $	$ {fd ^ 2} $	$ {fd ^ 3} $	$ {fd ^ 4} $
100-200	1	110	-3	-3	9	-27	81 год
120-200	2	130	-2	-4	8	-16	32
140-200	6	150	-1	-6	6	-6	6
160-200	20	170	0	0	0	0	0
180-200	11	190	1	11	11	11	11
200-200	3	210	2	6	12	24	48
220-200	2	230	3	6	18	54	162
	$ {N = 45} $			$ {\ sum fd = 10} $	$ {\ sum fd ^ 2 = 64} $	$ {\ sum fd ^ 3 = 40} $	$ {\ sum fd ^ 4 = 330} $

Поскольку отклонения были взяты от предполагаемого среднего значения, мы сначала вычисляем моменты относительно произвольного начала, а затем моменты относительно среднего. Моменты о произвольном происхождении '170'

$ {\ mu_1 ^ 1 = \ frac {\ sum fd} {N} \ times i = \ frac {10} {45} \ times 20 = 4.44 \\ [7pt] \ mu_2 ^ 1 = \ frac {\ sum fd ^ 2} {N} \ times i ^ 2 = \ frac {64} {45} \ times 20 ^ 2 = 568,88 \\ [7pt] \ mu_3 ^ 1 = \ frac {\ sum fd ^ 2} {N} \ раз i ^ 3 = \ frac {40} {45} \ times 20 ^ 3 = 7111,11 \\ [7pt] \ mu_4 ^ 1 = \ frac {\ sum fd ^ 4} {N} \ times i ^ 4 = \ frac {330} {45} \ times 20 ^ 4 = 1173333,33} $

Моменты о среднем

$ {\ mu_2 = \ mu'_2 - (\ mu'_1) ^ 2 = 568,88- (4.44) ^ 2 = 549,16 \\ [7pt] \ mu_3 = \ mu'_3 - 3 (\ mu'_1) (\ mu'_2) + 2 (\ mu'_1) ^ 3 \\ [7pt] \, = 7111,11 - (4,44) (568,88) + 2 (4,44) ^ 3 \\ [7pt] \, = 7111,11 - 7577,48 + 175,05 = - 291.32 \\ [7pt] \\ [7pt] \ mu_4 = \ mu'_4 - 4 (\ mu'_1) (\ mu'_3) + 6 (\ mu_1) ^ 2 (\ mu'_2) -3 (\ mu'_1) ^ 4 \\ [7pt] \, = 1173333.33 - 4 (4.44) (7111.11) +6 (4.44) ^ 2 (568.88) - 3 (4.44) ^ 4 \\ [7pt] \, = 1173333.33 - 126293.31 + 67288.03-1165.87 \\ [7pt] \, = 1113162.18} $

Теперь, исходя из значения движения относительно среднего, мы можем вычислить $ {\ beta_1} $ и $ {\ beta_2} $:

$ {\ beta_1 = \ mu ^ 2_3 = \ frac {(- 291.32) ^ 2} {(549.16) ^ 3} = 0,00051 \\ [7pt] \ beta_2 = \ frac {\ mu_4} {(\ mu_2) ^ 2 } = \ frac {1113162.18} {(546.16) ^ 2} = 3,69} $

Из приведенных выше вычислений можно сделать вывод, что $ {\ beta_1} $, который измеряет асимметрию, почти равен нулю, что указывает на то, что распределение почти симметрично. $ {\ beta_2} $, который измеряет эксцесс, имеет значение больше 3, что означает лептокуртичность распределения.