Wie groß müsste ein QR-Code auf meinem Dach sein, damit ein Satellit ihn bei der heute zulässigen Auflösung scannen kann?

Jan 26 2021

Verwenden Sie beispielsweise die Planet Labs-Satelliten

Vielen Dank

Antworten

7 uhoh Jan 28 2021 at 04:55

Wie groß müsste ein QR-Code auf meinem Dach sein, damit ein Satellit ihn bei der heute zulässigen Auflösung scannen kann?

Verwenden Sie beispielsweise die Planet Labs-Satelliten

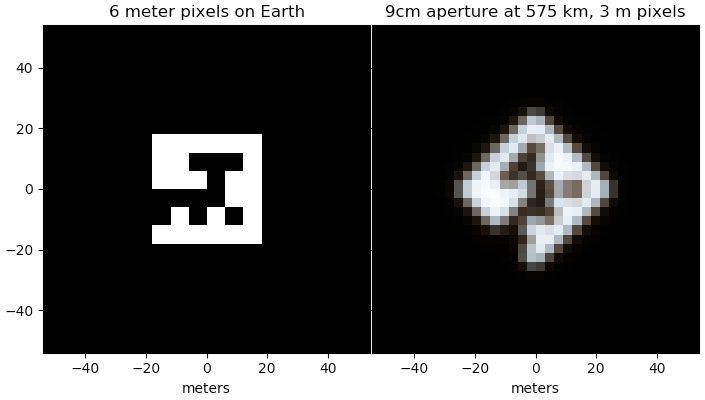
Dies ist eine ergänzende Antwort. Ich habe 6-Meter-QR-Pixel aus dem Weltraum mit einer 9-cm-Apertur (aus dem Ende eines 3U-Dove-Cubesat) bei Wellenlängen von 450, 550 und 650 nm simuliert, um 45 Grad gedreht und dann mit 3-Meter-Pixeln abgetastet.

Es ist ein schäbiges und zerbrechliches Skript, aber es macht den Job.

Das Bild unterstützt die Hauptschlussfolgerung in der anderen Antwort, dass dies wahrscheinlich die Mindestgröße für eine gewisse Zuverlässigkeit ist, um es mit einer Taube zu sehen.

Das Skript ist suboptimal, ich war faul und habe PIL zum Drehen verwendet, ich hätte interpolieren scipy.ndimage.map_coordinateskönnen und ich hätte mit "fuzzified" scipy.ndimage.gaussian_filteranstelle einer schicken Airy-Festplatte "fuzzifizieren" können .

Die Farbtöne im endgültigen Bild sind auf wellenlängenabhängige Beugungsgrenzen der Apertur zurückzuführen, die ungefähr $1.22 \lambda / D$ Variation der Winkelauflösung mit dem Verhältnis von Wellenlänge zu Apertur.

import numpy as np
import matplotlib.pyplot as plt
import itertools
from PIL import Image
from scipy import special as spe
from scipy.ndimage import convolve

N = 5*2

data = ('111111' + '110001' + '111011' +
        '000011' + '010101' + '111111')
data = np.array([int(x) for x in data]).reshape((6, 6))
data = np.pad(data, ((6, 6), (6, 6)))

img = np.zeros((N*18, N*18, 3))

for i, j in itertools.product(np.arange(18), repeat=2):
    img[N*i:N*(i+1), N*j:N*(j+1)] = data[i, j]

pixsize = 6 # meters
scale = pixsize/N
extent = 9*N * scale * np.array([-1, 1, -1, 1])

R = 575 * 1000. # meters distance
x = 4*N * scale * np.linspace(-1, 1, 8*N)
X, Y = np.meshgrid(x, x)
q = np.sqrt(X**2 + Y**2)
wavelengths = 1E-09 * np.array([650, 550, 450])

a = 0.045 # radius of aperture in meters (looking out end of a 3U cubesat)
x = (2 * np.pi * a / wavelengths) * (q[..., None] / R)

# https://en.wikipedia.org/wiki/Airy_disk
airy = (2 * spe.j1(x) / x)**2
areas = airy.sum(axis=0).sum(axis=0)
airy /= areas

new = [convolve(img[..., i], airy[..., i]) for i in range(3)]
newarray = np.stack(new, axis=2)
newarray = np.uint8(255 * newarray/newarray.max())

newimg = Image.fromarray(newarray)
newimg45 = newimg.rotate(45)
newimg45.show()
n45 = np.array(list(newimg45.getdata())).reshape(18*2, N>>1, 18*2, N>>1, 3)
n45 = np.uint8(n45.sum(axis=(1, 3)) / (N>>1)**2)

if True:
    plt.figure()
    plt.subplot(1, 2, 1)
    plt.imshow(img, extent=extent)
    plt.title('6 meter pixels on Earth')
    plt.xlabel('meters')
    plt.subplot(1, 2, 2)
    plt.imshow(n45, extent=extent)
    plt.title('9cm aperture at 575 km, 3 m pixels')
    plt.xlabel('meters')
    plt.show()

4 uhoh Jan 27 2021 at 08:30

Wie groß müsste ein QR-Code auf meinem Dach sein, damit ein Satellit ihn bei der heute zulässigen Auflösung scannen kann?

Verwenden Sie beispielsweise die Planet Labs-Satelliten

tl; dr: Wenn Sie das in @ CamilleGoudeseunes Antwort beschriebene 6x6 " Augmented Reality Tag " verwenden, wie das auf dem Curiosity Rover und 6-Meter-Pixel (doppelte Mindestauflösung, um eine willkürliche Übersetzung und Drehung zu ermöglichen) , sollte Ihr Muster 36 x 36 Meter groß sein , um ein zu haben Gute Abwechslung beim Erkennen und Wiederherstellen eines Bildes von einer PlanetLabs-Taube.

Ich würde das rote und infrarote Reflexionsvermögen aus den hellen Bereichen entfernen und nur in den kürzeren Wellenlängen codieren, da die Tauben vier Farbkanäle haben, die (wahrscheinlich) beugungsbegrenzt sind und längere Wellenlängen dann möglicherweise eine schlechtere Auflösung haben.

Versuchen Sie, nur die kürzeren Wellenlängenbänder Ihres Zielraumfahrzeugs anzuregen, damit sie für gelegentliche Betrachter "herausspringen", oder betrachten Sie diese Wellenlängen im endgültigen Datenprodukt nur, wenn Sie nach sich selbst suchen.

Beim https://www.planet.com/products/planet-imagery/Die zahlreichsten Satelliten oder "Tauben" liefern Daten für das Datenprodukt PLANETSCOPE. Die Satelliten sollen eine Auflösung von 3,7 Metern haben und das Datenprodukt eine neu abgetastete Pixelgröße von 3 Metern. Siehe auch die Antwort von @ djr auf Sind diese Bilder von Planet Labs? Sind die Bilder öffentlich verfügbar?

Wenn Sie unglaublich viel Glück hatten, dass die Pixel sowohl translatorisch als auch rotatorisch mit Ihrem QR-Muster ausgerichtet waren, könnten sie theoretisch 3 Meter betragen.

In der Praxis sollten Sie bei einer willkürlichen Verschiebung und Drehung Ihres Musters innerhalb des Bildfelds einen Faktor von mindestens 2, wenn nicht 3 größer als diesen haben.

@Uwe erinnert uns daran, dass ein kleiner QR-Code immer noch ziemlich groß wäre. Es gibt 11 x 11 Micro-QR-Codes und Spacefolks haben noch kleinere Pixelzahlen für Alternativen zu QR-Codes mit noch weniger Pixeln verwendet.