Wilson-Effekt: Wie „tief“ sind Sonnenflecken?
Ich habe kürzlich vom Wilson-Effekt der Sonnenatmosphäre erfahren . Der Saas-Fee-Aufbaukurs 2009 39 besagt:
In der Nähe des Sonnenrandes verschwinden der Kernschatten [der kreisförmige dunkle Bereich eines Sonnenflecks] und der mittelseitige Halbschatten [der hellere Rand des Sonnenflecks]. Wir sehen$400-800{\rm km}$ tiefer in Sonnenflecken als in der Photosphäre.
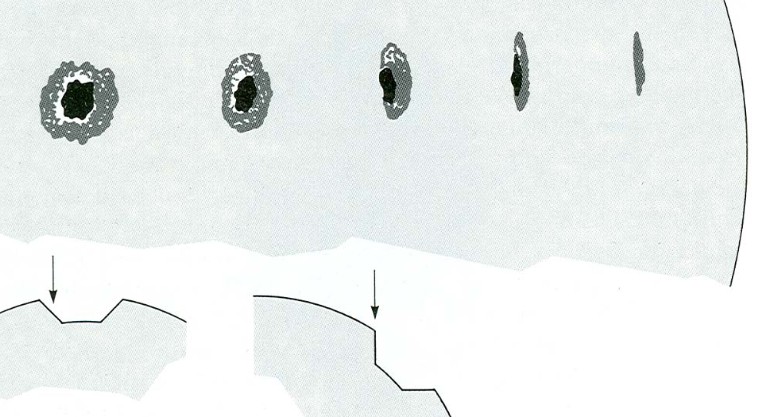
Dann gibt es eine Publikation mit dem Titel Der Sonnenfleck – seicht oder tief? von Solov'ev und Kirichek aus dem Jahr 2014, die in der Zusammenfassung sagt:
Zwei Sonnenfleckenmodelle werden verglichen - flach und tief. Nach ersterem dringt ein Sonnenfleck als ein von einem starken regulären Feld und vergleichsweise kaltem Plasma besetzter Bereich bis zu einer geringen Tiefe von etwa 4 mm in die solare Konvektionszone ein. […]
Außerdem gibt es eine Dissertation von Benjamin Beeck aus dem Jahr 2015, die zB folgende Grafik zeigt:
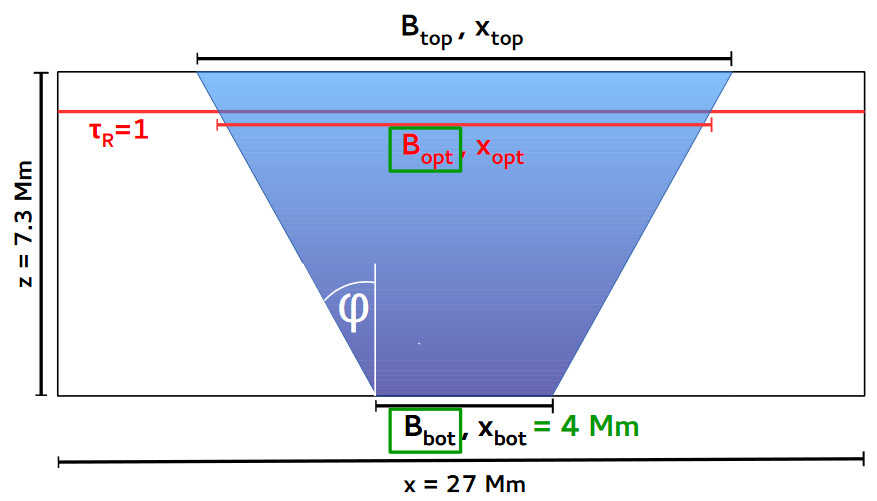
Mit anderen Worten, ich habe Werte zwischen $400 \ldots 7300 {\rm km}=7.3 {\rm Mm}$für die Tiefen eines Sonnenflecks, was mich etwas verwirrt - ich würde mich freuen, wenn mir jemand die recht große Bandbreite der Tiefen erklären könnte. Zum einen interessiert mich die Tiefe des Kernschattens gemessen vom Halbschatten (sofern er als flach angesehen werden kann), zum anderen möchte ich auch den Abstand vom Halbschatten bis zum Ende des ( sichtbare) Photosphäre, alles idealerweise mit Fehlerbalken.
Antworten
Interessante Fragen! Ich hoffe, ich kann etwas Sonnenlicht auf sie werfen.
Wie in der von Ihnen zitierten Zusammenfassung erwähnt, ist das Verständnis und die Modellierung von Sonnenflecken eine offene Frage , insbesondere die Frage, wie die Stabilität von Sonnenflecken aufrechterhalten wird.
Es gibt viele Modelle, wie Ihre Zitate zeigen. Zunächst eine terminologische Klarstellung: Der "Wilson-Effekt" ist heute im Wesentlichen ein Modell zur Erklärung der Physik des Sonnenflecks. Die „Wilson-Depression“ ist ein beobachtbarer Bestandteil eines Sonnenflecks: Die geometrische Höhe der sichtbaren Sonnenoberfläche ist im Vergleich zum Rest der Sonne tiefer. Zur Zeit Wilsons war dies eine Hypothese, aber solche Depressionen wurden gemessen, siehe z. B. die Abbildung hier. Da der Sonnenfleck im Prinzip durch konvektive Aktivität unterhalb der Photosphäre erzeugt wird (dh der konvektive Wärmetransport wird durch starke Magnetfelder blockiert, weshalb starke Magnetfelder benötigt werden, um einen stabilen Sonnenfleck zu erhalten), könnte der Sonnenfleck im Prinzip viel tiefer als das, was wir beobachten können, da wir nicht direkt unter die Photosphäre sehen können (da das Plasma der Sonne zu undurchsichtig wird).
Es gibt andere Modelle, um die Depression eines Sonnenflecks zu erklären. Beispielsweise minimiert ein neueres Modell , das (anscheinend) frei von systematischen Unsicherheiten ist, da keine modellabhängigen Annahmen vorliegen, die Divergenz des Magnetfelds, die aus spektropolarimetrischen Beobachtungen abgeleitet wird. Indem sie ihren Rahmen auf Beobachtungen eines Sonnenflecks anwenden, stellen sie fest:
Die abgeleitete Wilson-Depression (∼600 km) stimmt mit Ergebnissen überein, die typischerweise aus dem Wilson-Effekt gewonnen werden.
Ihre Ergebnisse stimmen mit denen von Studien überein, die den Wilson-Effekt verwenden, wie Sie z. B. aus dem Saas-Fee-Aufbaukurs 2009 39 zitieren.
Also deine Fragen:
Ich würde mich freuen, wenn mir jemand den recht großen Tiefenbereich erklären könnte. Zum einen interessiert mich die Tiefe des Kernschattens gemessen vom Halbschatten (wenn er als flach angesehen werden kann), zum anderen möchte ich auch den Abstand vom Halbschatten bis zum Ende des ( sichtbare) Photosphäre, alles idealerweise mit Fehlerbalken.
Um einen Plot mit genaueren Antworten und Fehlerbalken zu erstellen, würde jemand bereits einen solchen Plot erstellt haben, oder ich müsste einen erstellen. Ich selbst habe dazu keine Zeit, und ich kann keine veröffentlichte Arbeit damit finden (es könnte dort draußen sein). Also versuche ich es konzeptioneller zu erklären. Außerdem können wir nicht unter die Photosphäre sehen, daher müssen meines Erachtens indirekte Methoden verwendet werden, um Fehlerbalken bei Beobachtungen der Tiefe des Kernschattens zu erhalten, die ich nur schwer finden kann (und bezweifle, dass dies bereits geschehen ist! EDIT: siehe sehr letzter Absatz über Helioseismologie).
In dem Wiki- Artikel heißt es: "Das Ausmaß der Vertiefung ist schwer zu bestimmen, kann aber bis zu 1.000 km betragen." Aber es zitiert diese Behauptung nicht ;)
Modelle des Wilson-Effekts, wie die von Ihnen zitierten, versuchen die Entstehung eines Sonnenflecks so zu erklären, dass er aus der konvektiven Hülle des Sterneninneren stammt. Ist das vernünftig?: die zitierte Tiefe von$\sim 7.3$Mm für diese Anschwellen des Plasmas liegen mindestens innerhalb des Sonnenradius, der $\sim 10^9$m = 1 Gramm. Die Photosphäre ist die tiefste im Inneren der Sonne, die wir optisch sehen können, und erstreckt sich auf etwa 4x10$^5$m. Es ist also vorstellbar, dass der Sonnenfleck in Tiefen unterhalb der Photosphäre innerhalb eines konvektiven Bereichs der Sonne existieren kann, ohne dass der Boden des Sonnenflecks zu tief ist.
ADDED EDIT: In den Modellen von Solov'ev und Kirichek, z 4000 G. Die Tiefe der Wilson-Senke wächst linear mit B. Der Bereich stabiler Gleichgewichte ist so begrenzt, dass größere Sonnenflecken (Radius größer als etwa 12–18 mm) instabil sind, was das Fehlen sehr großer Sonnenflecken auf . erklären könnte der Sonne, sowie das Erscheinen der Lichtbrücken in großen Sonnenflecken, die sie in mehrere Teile unterteilen. Sonnenflecken mit B im Bereich von 2,6–2,7 kg und einem Umbralradius von etwa 2 mm sind am stabilsten.“ Zitat aus Anmerkung 4 davon entnommen Helioseismology Review (auch im letzten Absatz unten) und siehe Abbildung 22 dieses Reviews für eine schematische Darstellung ihres Modells.
In der von Ihnen zitierten These von B. Beeck, dem hier gefundenen Hauptartikel , ist die Geometrie des Kernschattens (noch des Halbschattens) NICHT von vornherein bekannt, daher machen sie Vermutungen und überprüfen sie mit ihren detaillierten numerischen Simulationen. Sie variieren systematisch die Anfangsbedingungen, Randbedingungen, die magnetische Feldstärke und die Tiefe des Sonnenflecks, um einen physikalisch stabilen Sonnenfleck zu erzeugen. Sie finden:
Stabile Sonnenflecken erfordern ein Magnetfeld von > 4kG in den unterirdischen Schichten. Die Struktur (zB T-Gradient) unterhalb von z~2-3 Mm scheint für die Stabilität von Sonnenflecken wichtig zu sein. Dies deutet auch darauf hin, dass Sonnenflecken keine sehr flachen Phänomene sein können. Daraus schließen sie: Stabile Sonnenflecken brauchen in Tiefen von 5-6 mm ein Magnetfeld von B ≥ 6 kG.
Sie spekulieren, dass diese Stabilitätsanforderung flache (dh nicht tiefe) Sonnenfleckengeometrien ausschließen kann. Sie versuchen dies mit der Keil-/Plattengeometrie zu quantifizieren, bei der eine höhere Magnetfeldstärke am unteren Rand des Sonnenflecks zu einer geringeren Umbraintensität und einer ausgeprägteren Halbschatten führt (siehe 5. Folie von Ende), was verwendet werden könnte, um bestimmte beobachtungsbedingt auszuschließen Sonnenfleckengeometrien.
ADDED EDIT: Die hier beteiligten Skalen sind also Teil eines aktiven Forschungsgebiets. Es gibt viele theoretische Gründe für die Annahme, dass die Sonnenflecken tief und groß in der Größenordnung von ~Mm sein können, aber wir können die Sonne nur so tief untersuchen, sodass wir uns normalerweise darauf beschränken, nur in der Größenordnung von ~ . zu sehen$10^5$m, was mit der Tiefe der Photosphäre übereinstimmt. Dies führt dazu, dass die genaue Struktur und Tiefe des Kernschattens und des Halbschattens derzeit nicht gut verstanden wird, obwohl die Abhängigkeit von verschiedenen Parametern innerhalb bestimmter Rahmen gut verstanden wird.
Direkt nachdem ich diese Antwort gepostet hatte, wurde mir klar, dass die Helioseismologie eine Möglichkeit ist, das Problem der Sondierung tiefer als die Photosphäre zu umgehen, und es scheint vielversprechend zu sein! Fortschritte in der Helioseismologie haben lange Einblicke in das Innere der Sonne erwartet, zum Beispiel hier und hier , die vergleichbare Schätzungen für die Tiefe von Sonnenflecken ergeben haben, d$\sim$1 mm. Ich denke, dies ist ein aktives Forschungsgebiet und es wird gut sein, seine Entwicklung zu verfolgen. Sehen Sie hier für eine (halb-)neue Rezension.