Kann der Stern-Brocot-Baum zur besseren Konvergenz von eingesetzt werden? $2^m/3^n$?
Lesevoraussetzung:
- Kann irgendein positiver Real als angenähert werden? $2^m/3^n$ mit $(m,n)$ groß genug?
- Stern Brocot Baumsequenz
Grund, warum ich nach einem Verfahren gesucht habe, das diesen Nachteil nicht aufweist, dh bei dem die nächste Annäherung immer näher am gewünschten Ergebnis liegt. Das habe ich bisher versucht.
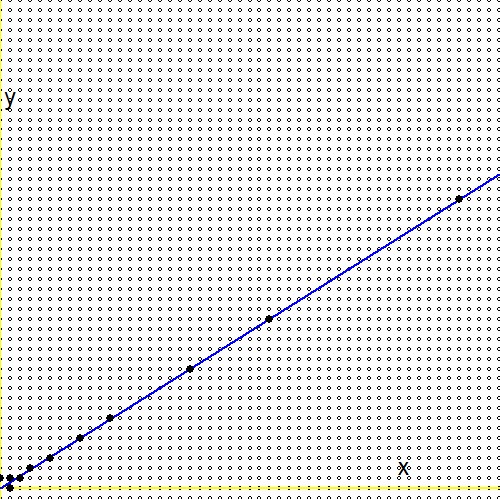
Nach Frage (2.) für jede positive reelle Zahl$0 \lt g \lt 1$gibt es eine unendliche Folge im Stern Brocot-Baum [..], die gegen die reelle Zahl konvergiert. In der Zwischenzeit hat diese Frage eine Antwort und das Hauptergebnis lautet wie folgt: $$ - \frac{1}{n_1(n_1+n_2)} \lt g - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} $$ In Anbetracht von Frage (1.) ersetzen wir $\ln(2)/\ln(3)$ für diese Nummer $g$. Dann folgt daraus: $$ - \frac{1}{n_1(n_1+n_2)} \lt \frac{\ln(2)}{\ln(3)} - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} \\ - \frac{\ln(3)}{n_1} \lt \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \lt + \frac{\ln(3)}{n_2} \\ \ln\left(3^{-1/n_1}\right) \lt \ln\left(\frac{2^{n_1+n_2}}{3^{m_1+m_2}}\right) \lt \ln\left(3^{+1/n_2}\right) \\ 3^{-1/n_1} \lt \frac{2^{n_1+n_2}}{3^{m_1+m_2}} \lt 3^{+1/n_2} $$Die Suche durch den Stern-Brocot-Baum kann abgebildet werden. Die blaue Linie ist die Funktion $\,\color{blue}{x\ln(2)-y\ln(3)=0}\,$, kleine Kreise sind Brüche, die auf einem Gitter abgebildet sind $\,m/n \to (m,n)\,$Massiv schwarz gefüllte Punkte sind die Fraktionen im Stern-Brocot-Baum. Es ist ersichtlich, dass das Durchsuchen des Baums viel effizienter ist als das Erhöhen $m$ und $n$ mit Schritten nacheinander.
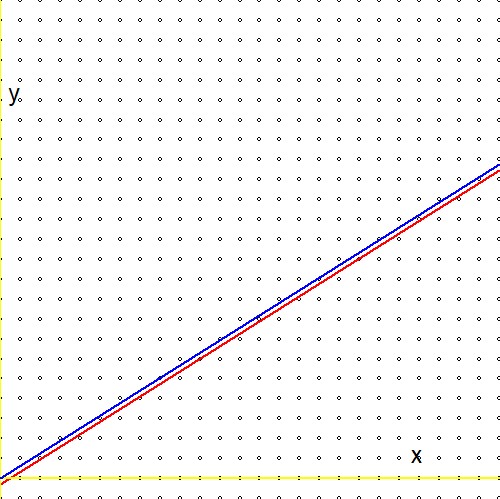
Vergleichen Sie nun den Ausdruck in der zweiten Zeile der obigen Formeln mit einem analogen Ausdruck in Referenz (1.): $$ \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \quad \Longleftrightarrow \quad m\ln(2) - n\ln(3) - \ln(r) $$ Und seien Sie auf eine Enttäuschung vorbereitet: den Logarithmus des willkürlichen Realen $r$wird vermisst! Oder alternativ:$\ln(r)=0$ oder $r=1$. Dies bedeutet, dass unsere "unendliche Suche" durch den Stern-Brocot-Baum, obwohl hocheffizient, letztendlich nur für die Nummer eins zu einer Annäherung kommt. Ich finde das seltsam, weil es - grafisch gesehen - keinen großen Unterschied zwischen zu geben scheint$\color{red}{2^m/3^n \to r}$ und $\color{blue}{2^m/3^n \to 1}$::
Daher die FRAGE: Gibt es ein Mittel, um das Stern-Brocot-Verfahren so anzupassen, dass es für andere Realitäten als eine funktioniert?
BEARBEITEN.
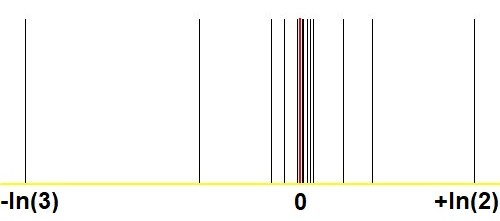
Hier kommt eine weitere Grafik, die die erstaunliche Konvergenz mit der Stern-Brocot-Methode im Vergleich zu analogen Bildern in meinen Fragen und Antworten zeigt$2^m/3^n$ mit $(m,n)$groß genug? ::
Antworten
Ich werde einen Ansatz geben, der das Stern-Brocot-Verfahren nicht verwendet.
Es reicht aus, das zu zeigen $\frac{2^{m}}{3^{n}}$ist im Intervall dicht [1,2]. Seit der Einnahme$\alpha\in (0,\infty)$ außerhalb dieses Intervalls gibt es einige $k\in Z$ so dass $\alpha = 2^{k}\gamma $ für einige $\gamma \in [1,2]$. Dann wissen wir, dass es eine Sequenz in gibt$\frac{2^{m}}{3^{n}}$ welche Ansätze $\gamma$Multiplizieren der Sequenz termweise mit $2^{k}$ (möglicherweise einen Schwanz der Sequenz nehmen), erhalten wir eine Sequenz in $\frac{2^{m}}{3^{n}}$ welche Ansätze $\alpha$.
Als nächstes betrachten wir die Karte $f:[1,2] -> [0,1]$ mit $f(x) = log_{2}(x)$ ist eine Bijektion.
Das Bild von $\frac{2^{m}}{3^{n}}$ unter der Karte ist $N-Nlog_{2}(3)$. Es reicht also aus, das zu zeigen$N-Nlog_{2}(3)$ ist dicht in $[0,1]$.
Dies ist eine Folge des Weylschen Gleichverteilungssatzes, der ein Sonderfall des Ergodischen Satzes ist.
Erwägen $a=2-log_{2}(3) = log_{2}(\frac{4}{3})$, so $a$ ist im Bild des Sets, so ist $na = log_{2}(\frac{4^{n}}{3^{n}})$ und so ist der Bruchteil von $na$.
Der Satz der Weyl-Gleichverteilung (der kein triviales Ergebnis ist) zeigt, dass für irrational a der Bruchteil von $na$ist gleichmäßig verteilt und daher dicht auf [0,1]. Schon seit$2-log_{2}(3)$ ist irrational, können Sie diesen Satz verwenden.