Dapatkah pohon Stern-Brocot digunakan untuk konvergensi yang lebih baik $2^m/3^n$?
Bacaan prasyarat:
- Dapatkah riil positif apa pun didekati sebagai $2^m/3^n$ dengan $(m,n)$ cukup besar?
- Urutan pohon Brocot buritan
Alasan mengapa saya telah mencari prosedur yang tidak memiliki kelemahan ini, yaitu di mana perkiraan berikutnya selalu lebih dekat dengan hasil yang diinginkan. Inilah yang sudah saya coba selama ini.
Menurut pertanyaan (2.), untuk setiap bilangan riil positif$0 \lt g \lt 1$, terdapat urutan tak hingga dalam pohon Stern Brocot [..] yang menyatu dengan bilangan real. Sementara itu, pertanyaan ini memiliki jawaban , dan hasil utamanya berbunyi sebagai berikut: $$ - \frac{1}{n_1(n_1+n_2)} \lt g - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} $$ Mengingat pertanyaan (1.), kami menggantinya $\ln(2)/\ln(3)$ untuk nomor itu $g$. Maka berikut ini: $$ - \frac{1}{n_1(n_1+n_2)} \lt \frac{\ln(2)}{\ln(3)} - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} \\ - \frac{\ln(3)}{n_1} \lt \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \lt + \frac{\ln(3)}{n_2} \\ \ln\left(3^{-1/n_1}\right) \lt \ln\left(\frac{2^{n_1+n_2}}{3^{m_1+m_2}}\right) \lt \ln\left(3^{+1/n_2}\right) \\ 3^{-1/n_1} \lt \frac{2^{n_1+n_2}}{3^{m_1+m_2}} \lt 3^{+1/n_2} $$Pencarian melalui pohon Stern-Brocot bisa digambarkan. Garis biru adalah fungsinya $\,\color{blue}{x\ln(2)-y\ln(3)=0}\,$, lingkaran kecil adalah pecahan, dipetakan pada kotak $\,m/n \to (m,n)\,$, titik-titik besar berwarna hitam adalah pecahan di pohon Stern-Brocot. Terlihat bahwa pencarian melalui pohon jauh lebih efisien daripada meningkatkan $m$ dan $n$ dengan penambahan satu per satu.
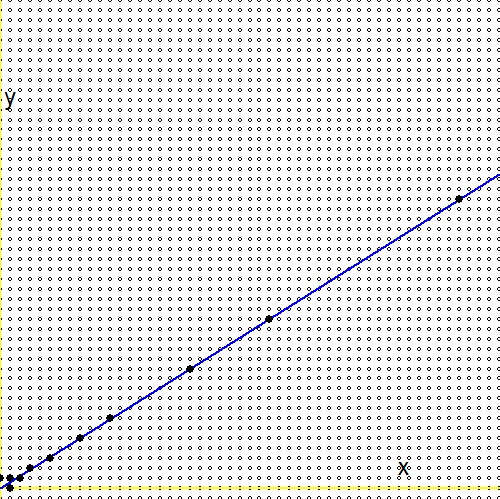
Sekarang bandingkan ekspresi pada baris kedua dari rumus di atas dengan ekspresi analog dalam referensi (1.): $$ \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \quad \Longleftrightarrow \quad m\ln(2) - n\ln(3) - \ln(r) $$ Dan bersiaplah untuk kekecewaan: logaritma nyata yang sewenang-wenang $r$hilang! Atau sebagai alternatif:$\ln(r)=0$ atau $r=1$. Ini berarti bahwa "pencarian tak terbatas" kita melalui pohon Stern-Brocot, meskipun sangat efisien, akhirnya sampai pada perkiraan hanya untuk nomor satu. Menurut saya ini aneh, karena - secara grafis - sepertinya tidak ada perbedaan besar di antara keduanya$\color{red}{2^m/3^n \to r}$ dan $\color{blue}{2^m/3^n \to 1}$:
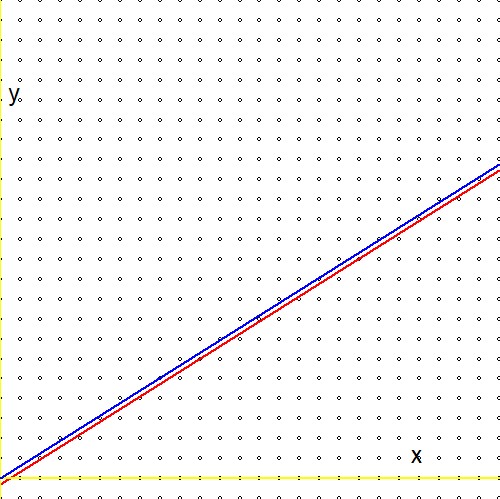
Oleh karena itu, PERTANYAAN: apakah ada cara untuk mengadaptasi prosedur Stern-Brocot sedemikian rupa sehingga berfungsi untuk real selain satu?
EDIT.
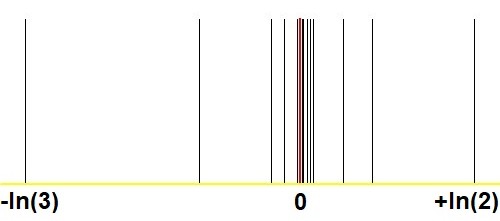
Di sinilah grafik lain yang menunjukkan konvergensi yang menakjubkan dengan metode Stern-Brocot, dibandingkan dengan gambar analog di Tanya Jawab saya. Dapatkah riil positif diperkirakan sebagai$2^m/3^n$ dengan $(m,n)$cukup besar? :
Jawaban
Saya akan memberikan pendekatan yang tidak menggunakan prosedur Stern-Brocot.
Itu sudah cukup untuk menunjukkan itu $\frac{2^{m}}{3^{n}}$padat dalam interval [1,2]. Sejak mengambil$\alpha\in (0,\infty)$ di luar interval ini ada beberapa $k\in Z$ yang seperti itu $\alpha = 2^{k}\gamma $ untuk beberapa $\gamma \in [1,2]$. Lalu kita tahu ada urutan masuk$\frac{2^{m}}{3^{n}}$ yang mendekati $\gamma$, mengalikan urutan menurut jarum jam dengan $2^{k}$ (mungkin mengambil ekor dari urutan), kita mendapatkan urutan dalam $\frac{2^{m}}{3^{n}}$ yang mendekati $\alpha$.
Selanjutnya pertimbangkan itu peta $f:[1,2] -> [0,1]$ dengan $f(x) = log_{2}(x)$ adalah kebijaksanaan.
Gambar dari $\frac{2^{m}}{3^{n}}$ di bawah peta adalah $N-Nlog_{2}(3)$. Jadi cukup menunjukkan itu$N-Nlog_{2}(3)$ padat $[0,1]$.
Ini adalah konsekuensi dari Teorema Persamaan Weyl, yang merupakan kasus khusus dari Teorema Ergodik.
Mempertimbangkan $a=2-log_{2}(3) = log_{2}(\frac{4}{3})$, jadi $a$ adalah gambar dari himpunan, begitu juga $na = log_{2}(\frac{4^{n}}{3^{n}})$ dan begitu juga bagian pecahan dari $na$.
Teorema Persamaan Weyl (yang bukan merupakan hasil sepele) menunjukkan bahwa untuk irasional bagian pecahan dari $na$didistribusikan secara seragam dan karenanya padat pada [0,1]. Sejak$2-log_{2}(3)$ tidak rasional Anda dapat menggunakan teorema ini.