スターン・ブロコットの木を採用して、 $2^m/3^n$?
前提条件の読み物:
- 正の実数は次のように近似できますか $2^m/3^n$ と $(m,n)$ 十分大きい?
- スターンブロコットツリーシーケンス
この欠点がない手順、つまり次の近似が常に望ましい結果に近い手順を探していた理由。これは私がこれまでに試したことです。
質問(2.)によると 、すべての正の実数に対して$0 \lt g \lt 1$、スターンブロコットツリー[..]には、実数に収束する無限のシーケンスが存在します。一方、この質問に は答えがあり、そこでの主な結果は次のようになります。 $$ - \frac{1}{n_1(n_1+n_2)} \lt g - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} $$ 質問(1.)を考慮して、 $\ln(2)/\ln(3)$ その数のために $g$。次に、次のようになります。 $$ - \frac{1}{n_1(n_1+n_2)} \lt \frac{\ln(2)}{\ln(3)} - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} \\ - \frac{\ln(3)}{n_1} \lt \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \lt + \frac{\ln(3)}{n_2} \\ \ln\left(3^{-1/n_1}\right) \lt \ln\left(\frac{2^{n_1+n_2}}{3^{m_1+m_2}}\right) \lt \ln\left(3^{+1/n_2}\right) \\ 3^{-1/n_1} \lt \frac{2^{n_1+n_2}}{3^{m_1+m_2}} \lt 3^{+1/n_2} $$スターン・ブロコットの木の探索を描くことができます。青い線は機能です $\,\color{blue}{x\ln(2)-y\ln(3)=0}\,$、小さな円は分数であり、グリッドにマッピングされます $\,m/n \to (m,n)\,$、非常に黒い塗りつぶされたドットは、スターンブロコットツリーの分数です。ツリーを検索する方が、増やすよりもはるかに効率的であることがわかります。 $m$ そして $n$ 一度に1つずつ増分します。
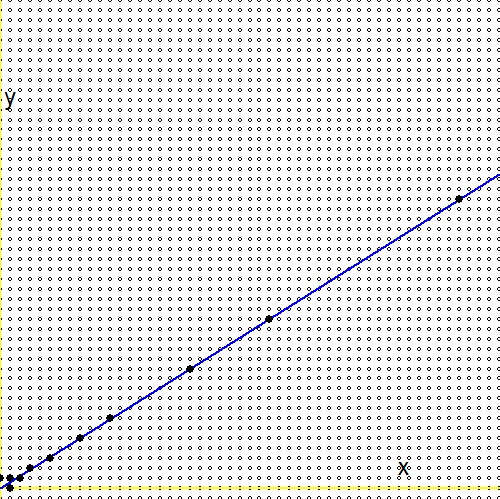
次に、上記の式の2行目の式を、参照(1.)の類似の式と比較します。 $$ \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \quad \Longleftrightarrow \quad m\ln(2) - n\ln(3) - \ln(r) $$ そして失望に備えてください:任意の実数の対数 $r$不足している!または代わりに:$\ln(r)=0$ または $r=1$。これは、Stern-Brocotツリーを介した「無限検索」は、非常に効率的ですが、最終的には1番目の近似値に到達することを意味します。私はこれが奇妙だと思います。なぜなら、グラフィカルに、両者の間に大きな違いはないように思われるからです。$\color{red}{2^m/3^n \to r}$ そして $\color{blue}{2^m/3^n \to 1}$:
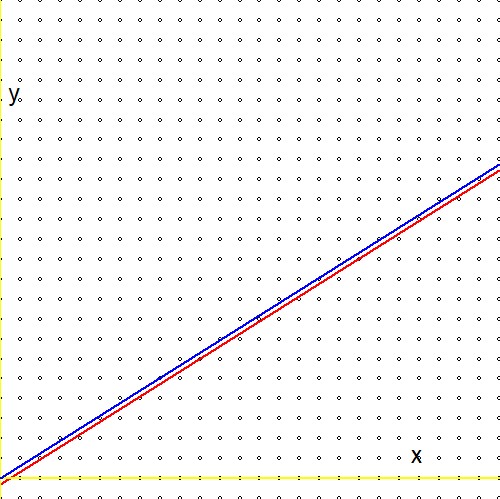
したがって、質問:1つ以外の実数で機能するようにStern-Brocot手順を適応させる手段はありますか?
編集。
これは、私のQ&Aの類似の写真と比較して、スターンブロコット法による驚くべき収束を示す別のグラフです。 正の実数は次のように近似できますか?$2^m/3^n$ と $(m,n)$十分大きい?:
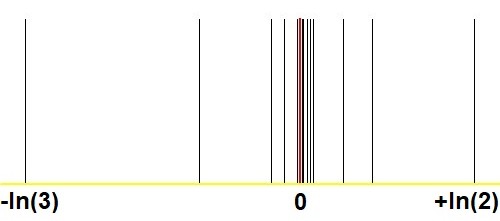
回答
スターン・ブロコット法を使用しないアプローチを紹介します。
それを示すだけで十分です $\frac{2^{m}}{3^{n}}$区間[1,2]で密です。取ってから$\alpha\in (0,\infty)$ この間隔の外にいくつかあります $k\in Z$ そのため $\alpha = 2^{k}\gamma $ いくつかのための $\gamma \in [1,2]$。次に、シーケンスがあることがわかります$\frac{2^{m}}{3^{n}}$ 近づく $\gamma$、シーケンスを項ごとに乗算します $2^{k}$ (おそらくシーケンスのテールを取る)、シーケンスを取得します $\frac{2^{m}}{3^{n}}$ 近づく $\alpha$。
次に、マップを検討します $f:[1,2] -> [0,1]$ と $f(x) = log_{2}(x)$ 全単射です。
の画像 $\frac{2^{m}}{3^{n}}$ 地図の下は $N-Nlog_{2}(3)$。だからそれを示すだけで十分です$N-Nlog_{2}(3)$ で密集しています $[0,1]$。
これは、エルゴード定理の特殊なケースであるワイルの同程度分布定理の結果です。
検討する $a=2-log_{2}(3) = log_{2}(\frac{4}{3})$、 そう $a$ セットの画像にあるので、 $na = log_{2}(\frac{4^{n}}{3^{n}})$ の小数部分もそうです $na$。
ワイル同程度分布定理(これは自明な結果ではありません)は、無理数の場合、 $na$は均一に分布しているため、[0,1]に密集しています。以来$2-log_{2}(3)$ この定理を使用できるのは不合理です。