浮動小数点演算は壊れていますか？

Question

次のコードについて考えてみます。

0.1 + 0.2 == 0.3  ->  false

0.1 + 0.2         ->  0.30000000000000004

なぜこれらの不正確さが起こるのですか？

Answer 1

バイナリ浮動小数点演算は次のようになります。ほとんどのプログラミング言語では、IEEE754標準に基づいています。問題の核心は、数値がこの形式で整数に2の累乗を掛けたものとして表されることです。（例えば、有理数0.1であり、1/10その分母正確に表現することができない2のべき乗ではありません）。

以下のために0.1標準でbinary64フォーマット、表現は正確のように記述することができます

• 0.1000000000000000055511151231257827021181583404541015625 10進数、または
• 0x1.999999999999ap-4でC99表記をhexfloat。

対照的に、である有理数0.1は1/10、次のように正確に書くことができます。

• 0.1 10進数、または
• 0x1.99999999999999...p-4C99 hexfloat表記の類似物で、...は9の終わりのないシーケンスを表します。

定数0.2と0.3あなたのプログラムではまた、彼らの真の値に近似されます。に最も近いdoubleもの0.2が有理数よりも大きい0.2が、最も近いdoubleもの0.3が有理数よりも小さい場合があり0.3ます。合計0.1とは、0.2合理的な数よりも大きい巻き取る0.3ので、あなたのコード内の定数で不同意します。

浮動小数点演算の問題のかなり包括的な取り扱いは、すべてのコンピューター科学者が浮動小数点演算について知っておくべきことです。わかりやすい説明については、floating-point-gui.deを参照してください。

補足：すべての位置（基数N）数値システムは、この問題を正確に共有します

単純な古い10進数（基数10）にも同じ問題があります。そのため、1/3のような数値は0.333333333になります。

たまたま10進法で表現するのは簡単ですが、2進法に適合しない数（3/10）に出くわしました。1/16は10進数（0.0625）の醜い数字ですが、2進数では、10進数（0.0001）の10,000分の1と同じくらいきれいに見えます**-私たちの日常生活で2進数システムを使用する習慣があると、その数字を見て、何かを半分にしたり、何度も何度も何度も半分にすることでそこに到達できることを本能的に理解するでしょう。

**もちろん、それは浮動小数点数がメモリに格納される方法とは異なります（科学的記数法の形式を使用します）。ただし、通常使用する「実世界」の数値は10の累乗であることが多いため、2進浮動小数点の精度エラーが発生する傾向があることを示しています。ただし、10進数システムを使用しているためです。今日。これが、「7つのうち5つ」ではなく71％のようなものを言う理由でもあります（5/7は10進数で正確に表すことができないため、71％は概算です）。

つまり、2進浮動小数点数は壊れていません。たまたま、他のすべての基数N記数法と同じくらい不完全です:)

サイドサイドノート：プログラミングでのフロートの操作

実際には、この精度の問題は、浮動小数点数を表示する前に、丸め関数を使用して、関心のある小数点以下の桁数に丸める必要があることを意味します。

また、同等性テストを、ある程度の許容範囲を許容する比較に置き換える必要があります。これは、次のことを意味します。

しないでくださいif (x == y) { ... }

代わりにif (abs(x - y) < myToleranceValue) { ... }。

ここabsで、は絶対値です。myToleranceValue特定のアプリケーションに合わせて選択する必要があります。これは、許容できる「ウィグルルーム」の量と、比較する最大数（精度の問題による）に大きく関係します。 ）。選択した言語の「イプシロン」スタイル定数に注意してください。これらは許容値として使用されません。

Answer 2

ハードウェア設計者の視点

私は浮動小数点ハードウェアを設計および構築しているので、これにハードウェア設計者の視点を追加する必要があると思います。エラーの原因を知ることは、ソフトウェアで何が起こっているかを理解するのに役立つ可能性があり、最終的には、これが浮動小数点エラーが発生し、時間の経過とともに蓄積するように見える理由を説明するのに役立つことを願っています。

1。概要

エンジニアリングの観点からは、浮動小数点の計算を行うハードウェアは、最後に1ユニットの半分未満のエラーで十分であるため、ほとんどの浮動小数点演算にはエラーの要素があります。したがって、多くのハードウェアは、浮動小数点除算で特に問題となる1回の操作で、最後に1ユニットの半分未満のエラーを生成するためにのみ必要な精度で停止します。単一の操作を構成するものは、ユニットが取るオペランドの数によって異なります。ほとんどの場合、2つですが、一部のユニットは3つ以上のオペランドを取ります。このため、エラーは時間の経過とともに増加するため、操作を繰り返すと望ましいエラーが発生するという保証はありません。

2.標準

ほとんどのプロセッサはIEEE-754標準に準拠していますが、一部のプロセッサは非正規化または異なる標準を使用しています。たとえば、IEEE-754には非正規化モードがあり、精度を犠牲にして非常に小さい浮動小数点数を表現できます。ただし、以下では、一般的な動作モードであるIEEE-754の正規化モードについて説明します。

IEEE-754標準では、ハードウェア設計者は、最後の場所で1ユニットの半分未満である限り、エラー/イプシロンの任意の値を許可され、結果は最後の1ユニットの半分未満である必要があります。 1回の操作のための場所。これは、操作が繰り返されるとエラーが増える理由を説明しています。IEEE-754倍精度の場合、これは54番目のビットです。これは、53ビットが浮動小数点数（たとえば、5.3e5の5.3）の仮数とも呼ばれる数値部分（正規化）を表すために使用されるためです。次のセクションでは、さまざまな浮動小数点演算でのハードウェアエラーの原因について詳しく説明します。

3.除算の丸め誤差の原因

浮動小数点除算のエラーの主な原因は、商の計算に使用される除算アルゴリズムです。ほとんどのコンピュータシステムは、主にZ=X/Y、で、逆数による乗算を使用して除算を計算しZ = X * (1/Y)ます。除算は繰り返し計算されます。つまり、各サイクルは、目的の精度に達するまで商の一部のビットを計算します。これは、IEEE-754の場合、最後に1単位未満の誤差を持つものです。Y（1 / Y）の逆数のテーブルは、低速除算では商選択テーブル（QST）と呼ばれ、商選択テーブルのビット単位のサイズは、通常、基数の幅、またはのビット数です。各反復で計算された商と、いくつかのガードビット。IEEE-754標準の倍精度（64ビット）の場合、除算器の基数のサイズにいくつかのガードビットkを加えたものになりk>=2ます。ここで。したがって、たとえば、一度に2ビットの商（基数4）を計算する除算器の一般的な商選択テーブルは、2+2= 4ビット（およびいくつかのオプションのビット）になります。

3.1除算の丸め誤差：逆数の近似

商選択テーブルの逆数は、除算方法によって異なります。SRT除算などの低速除算、またはゴールドシュミット除算などの高速除算。各エントリは、可能な限り最小のエラーを生成するために、除算アルゴリズムに従って変更されます。ただし、いずれの場合も、すべての逆数は実際の逆数の近似値であり、エラーの要素が発生します。低速除算と高速除算の両方の方法で商が繰り返し計算されます。つまり、各ステップで商のビット数が計算され、その結果が被除数から減算され、除算器は誤差が1の半分未満になるまでステップを繰り返します。最後にユニット。低速除算法は、各ステップで商の固定桁数を計算し、通常は構築に費用がかかりません。高速除算法は、ステップごとに可変桁数を計算し、通常、構築に費用がかかります。除算法の最も重要な部分は、それらのほとんどが逆数の近似による繰り返し乗算に依存しているため、エラーが発生しやすいことです。

4.他の操作での丸め誤差：切り捨て

すべての演算での丸め誤差のもう1つの原因は、IEEE-754で許可されている最終回答の切り捨てのさまざまなモードです。切り捨て、ゼロに丸める、最も近い丸め（デフォルト）、切り捨て、および切り上げがあります。すべてのメソッドは、1回の操作で最後に1ユニット未満のエラー要素を導入します。時間の経過と繰り返しの操作により、切り捨てによって結果のエラーも累積的に増加します。この切り捨てエラーは、何らかの形の繰り返し乗算を含むべき乗で特に​​問題になります。

5.繰り返し操作

浮動小数点計算を実行するハードウェアは、1回の操作で、最後に1ユニットの半分未満のエラーで結果を生成するだけでよいため、監視しないと、エラーは繰り返しの操作で大きくなります。これが、制限付きエラーを必要とする計算で、数学者がIEEE-754の最後の場所で最も近い偶数に丸めるなどの方法を使用する理由です。時間の経過とともにエラーが互いに打ち消し合う可能性が高くなるためです。と、IEEE 754丸めモードのバリエーションと組み合わせた区間演算を使用して、丸め誤差を予測し、それらを修正します。他の丸めモードと比較して相対誤差が小さいため、（最後の場所で）最も近い偶数桁に丸めるのがIEEE-754のデフォルトの丸めモードです。

デフォルトの丸めモードである、最後の場所で最も近い偶数に丸めるモードでは、1回の操作で最後の場所の1単位の半分未満のエラーが保証されることに注意してください。切り捨て、切り上げ、および切り捨てを単独で使用すると、最後の場所で1ユニットの半分より大きく、最後の場所で1ユニット未満のエラーが発生する可能性があるため、これらのモードは、そうでない限り推奨されません。区間演算で使用されます。

6.まとめ

要するに、浮動小数点演算のエラーの根本的な理由は、ハードウェアでの切り捨てと、除算の場合の逆数の切り捨ての組み合わせです。IEEE-754標準では、1回の操作で最後に1ユニットの半分未満のエラーしか必要としないため、繰り返し操作での浮動小数点エラーは、修正しない限り合計されます。

Answer 3

これは、基数2の場合とまったく同じように、10進数（基数10）の表記が破られます。

理解するには、1/3を10進値として表すことを考えてください。正確に行うことは不可能です！同様に、1/10（10進数の0.1）は、基数2（2進数）で「10進数」の値として正確に表すことはできません。小数点以下の繰り返しパターンは永遠に続きます。値は正確ではないため、通常の浮動小数点法を使用して正確な計算を行うことはできません。

Answer 4

ここでのほとんどの回答は、非常に乾燥した技術用語でこの質問に対処しています。普通の人間が理解できる言葉でこれに取り組みたいと思います。

あなたがピザをスライスしようとしていると想像してみてください。あなたはピザのスライスを正確に半分に切ることができるロボットのピザカッターを持っています。ピザ全体を半分にすることも、既存のスライスを半分にすることもできますが、いずれの場合も、半分は常に正確です。

そのピザカッターの動きは非常に細かく、ピザ全体から始めてそれを半分にし、毎回最小のスライスを半分にし続けると、スライスが小さすぎて高精度の能力が得られない前に、53回半分にすることができます。。その時点で、その非常に薄いスライスを半分にすることはできなくなりますが、そのまま含めるか除外する必要があります。

さて、ピザの10分の1（0.1）または5分の1（0.2）になるような方法で、すべてのスライスをどのようにつなぎ合わせますか？本当に考えて、試してみてください。神話上の精密ピザカッターが手元にあれば、本物のピザを試してみることができます。:-)

---

もちろん、ほとんどの経験豊富なプログラマーは本当の答えを知っています。つまり、どれほど細かくスライスしても、それらのスライスを使用してピザの正確な10分の1または5分の1をつなぎ合わせる方法はないということです。かなり良い近似を行うことができ、0.1の近似と0.2の近似を合計すると、0.3のかなり良い近似が得られますが、それでもそれは近似です。

倍精度の数値（ピザを53回半分にすることができる精度）の場合、0.1のすぐ下と大きい数値は、0.09999999999999999167332731531132594682276248931884765625と0.1000000000000000055511151231257827021181583404541015625です。後者は前者よりも0.1にかなり近いため、数値パーサーは0.1の入力が与えられると、後者を優先します。

（これら2つの数値の違いは、上向きのバイアスを導入する包含または下向きのバイアスを導入する除外のいずれかを決定する必要がある「最小スライス」です。その最小スライスの専門用語はulpです。）

0.2の場合、数値はすべて同じで、2倍に拡大されています。ここでも、0.2よりわずかに高い値を優先します。

どちらの場合も、0.1と0.2の近似にはわずかな上向きのバイアスがあることに注意してください。これらのバイアスを十分に追加すると、数値が必要な数値からさらに遠ざかります。実際、0.1 + 0.2の場合、バイアスが十分に高いため、結果の数値は最も近い数値ではなくなります。 0.3まで。

特に、0.1 +0.2は実際には0.1000000000000000055511151231257827021181583404541015625+ 0.200000000000000011102230246251565404236316680908203125 = 0.3000000000000000444089209850062616169452667236328125ですが、0.3に最も近い数値は実際には0.299999999999999988897769753748434595763683319091796875です。

---

PS一部のプログラミング言語では、スライスを正確に10分の1に分割できるピザカッターも提供されています。このようなピザカッターは一般的ではありませんが、アクセスできる場合は、スライスの10分の1または5分の1を正確に取得できることが重要な場合に使用する必要があります。

（元々はQuoraに投稿されました。）

Answer 5

浮動小数点の丸め誤差。0.1は、素因数5が欠落しているため、基数2では基数10ほど正確に表すことができません。1/ 3が10進数で表すのに無限の桁数を必要とするのと同じように、基数3では「0.1」です。 0.1は、基数10ではないのに対し、基数2では無限の桁数を取ります。そして、コンピュータには無限の量のメモリがありません。

Answer 6

他の正解に加えて、浮動小数点演算の問題を回避するために値のスケーリングを検討することをお勧めします。

例えば：

var result = 1.0 + 2.0;     // result === 3.0 returns true

... の代わりに：

var result = 0.1 + 0.2;     // result === 0.3 returns false

式0.1 + 0.2 === 0.3はfalseJavaScriptで返されますが、幸い浮動小数点での整数演算は正確であるため、スケーリングによって小数表現エラーを回避できます。

実用的な例として、精度が最優先される浮動小数点の問題を回避するために、¹セントの数を表す整数としてお金を処理することをお勧めします。ドルでは2550なくセントです25.50。

---

¹ Douglas Crockford：JavaScript：良い部分：付録A-ひどい部分（105ページ）。

Answer 7

私の答えはかなり長いので、3つのセクションに分けました。質問は浮動小数点数学に関するものなので、私はマシンが実際に何をするかを強調しました。また、倍精度（64ビット）に固有のものにしましたが、この引数はすべての浮動小数点演算に等しく適用されます。

前文

AN IEEE 754倍精度バイナリ浮動小数点形式（binary64）数は、フォームの数を表します。

値=（-1）^ s *（1.m ₅₁ m ₅₀ ... m ₂ m ₁ m ₀）₂ * 2 ^e-1023

64ビット：

• 最初のビットは符号ビットです。1数値が負の0場合、それ以外の場合は¹です。
• 次の11ビットは指数され、オフセットすなわち1023により、倍精度数の指数ビットを読んだ後、1023は、二つの電力を得るために減算されなければなりません。
• 残りの52ビットが仮数（又は仮数）。仮数では、バイナリ値の最上位ビットがであるため、「暗黙の」1.は常に²省略されます1。

¹ -IEEE 754は、符号付きゼロの概念を許可します-+0そして-0、異なる方法で処理され1 / (+0)ます。正​​の無限大です。1 / (-0)は負の無限大です。ゼロ値の場合、仮数ビットと指数ビットはすべてゼロです。注：ゼロ値（+0および-0）は、明示的に非正規化²として分類されません。

^2-これは、オフセット指数がゼロ（および暗黙的）である非正規化数には当てはまりません0.。デノーマル倍精度数の範囲をd_分≤| X | ≤D _maxのD、_最小（最小の表現の非ゼロの数）2れる^{-1023 - 51}（≈4.94×10 ^-324）及びd _maxの（仮数は、完全に構成されている最大の非正規化数、1s）は2であり、^{-1023 +} 1-2 ^-1023 --51（≈2.225* 10 ^-308）。

---

倍精度数を2進数に変換する

倍精度浮動小数点数を2進数に変換するオンラインコンバーターは多数存在しますが（binaryconvert.comなど）、倍精度数のIEEE 754表現を取得するためのサンプルC＃コードを次に示します（3つの部分をコロンで区切ります（:） ：

public static string BinaryRepresentation(double value)
{
    long valueInLongType = BitConverter.DoubleToInt64Bits(value);
    string bits = Convert.ToString(valueInLongType, 2);
    string leadingZeros = new string('0', 64 - bits.Length);
    string binaryRepresentation = leadingZeros + bits;

    string sign = binaryRepresentation[0].ToString();
    string exponent = binaryRepresentation.Substring(1, 11);
    string mantissa = binaryRepresentation.Substring(12);

    return string.Format("{0}:{1}:{2}", sign, exponent, mantissa);
}

---

要点：元の質問

（TL; DRバージョンの場合は下にスキップしてください）

Cato Johnston（質問者）は、なぜ0.1 + 0.2！= 0.3なのかと尋ねました。

バイナリで記述され（3つの部分をコロンで区切る）、値のIEEE754表現は次のとおりです。

0.1 => 0:01111111011:1001100110011001100110011001100110011001100110011010
0.2 => 0:01111111100:1001100110011001100110011001100110011001100110011010

仮数は、の繰り返し数字で構成されていることに注意してください0011。これは、計算にエラーがある理由の鍵です-0.1、0.2、および0.3は、1 / 9、1 / 3、または1/7を超える有限数のバイナリビットで正確にバイナリで表すことはできません。10進数。

また、指数の累乗を52減らし、バイナリ表現のポイントを52桁右にシフトできることにも注意してください（10 ^-3 * 1.23 == 10 ^-5 * 123のように）。これにより、バイナリ表現をa * ^2pの形式で表す正確な値として表すことができます。ここで、「a」は整数です。

指数を10進数に変換し、オフセットを削除し、暗黙の1（角括弧内）を再度追加すると、0.1と0.2は次のようになります。

0.1 => 2^-4 * [1].1001100110011001100110011001100110011001100110011010
0.2 => 2^-3 * [1].1001100110011001100110011001100110011001100110011010
or
0.1 => 2^-56 * 7205759403792794 = 0.1000000000000000055511151231257827021181583404541015625
0.2 => 2^-55 * 7205759403792794 = 0.200000000000000011102230246251565404236316680908203125

2つの数値を加算するには、指数が同じである必要があります。

0.1 => 2^-3 *  0.1100110011001100110011001100110011001100110011001101(0)
0.2 => 2^-3 *  1.1001100110011001100110011001100110011001100110011010
sum =  2^-3 * 10.0110011001100110011001100110011001100110011001100111
or
0.1 => 2^-55 * 3602879701896397  = 0.1000000000000000055511151231257827021181583404541015625
0.2 => 2^-55 * 7205759403792794  = 0.200000000000000011102230246251565404236316680908203125
sum =  2^-55 * 10808639105689191 = 0.3000000000000000166533453693773481063544750213623046875

合計は²ⁿ * 1. {bbb}の形式ではないため、指数を1増やし、10進数（2進数）のポイントをシフトして次のようにします。

sum = 2^-2  * 1.0011001100110011001100110011001100110011001100110011(1)
    = 2^-54 * 5404319552844595.5 = 0.3000000000000000166533453693773481063544750213623046875

仮数には53ビットがあります（53番目は上の行の角括弧内にあります）。IEEE 754のデフォルトの丸めモードは「最も近い値に丸める」です。つまり、数値xが2つの値aとbの間にある場合、最下位ビットがゼロである値が選択されます。

a = 2^-54 * 5404319552844595 = 0.299999999999999988897769753748434595763683319091796875
  = 2^-2  * 1.0011001100110011001100110011001100110011001100110011

x = 2^-2  * 1.0011001100110011001100110011001100110011001100110011(1)

b = 2^-2  * 1.0011001100110011001100110011001100110011001100110100
  = 2^-54 * 5404319552844596 = 0.3000000000000000444089209850062616169452667236328125

aとbは最後のビットだけが異なることに注意してください。...0011+ 1= ...0100。この場合、最下位ビットがゼロの値はbであるため、合計は次のようになります。

sum = 2^-2  * 1.0011001100110011001100110011001100110011001100110100
    = 2^-54 * 5404319552844596 = 0.3000000000000000444089209850062616169452667236328125

一方、0.3のバイナリ表現は次のとおりです。

0.3 => 2^-2  * 1.0011001100110011001100110011001100110011001100110011
    =  2^-54 * 5404319552844595 = 0.299999999999999988897769753748434595763683319091796875

これは、0.1と0.2の合計のバイナリ表現と^2-54だけ異なります。

0.1と0.2のバイナリ表現は、IEEE 754で許可されている数値の最も正確な表現です。デフォルトの丸めモードにより、これらの表現を追加すると、最下位ビットのみが異なる値になります。

TL; DR

ライティング0.1 + 0.2（三つの部分を分離するコロンで）IEEE 754バイナリ表現にし、それを比較する0.3（私は角括弧内の個別のビットを入れている）、これは次のとおりです。

0.1 + 0.2 => 0:01111111101:0011001100110011001100110011001100110011001100110[100]
0.3       => 0:01111111101:0011001100110011001100110011001100110011001100110[011]

10進数に戻すと、これらの値は次のようになります。

0.1 + 0.2 => 0.300000000000000044408920985006...
0.3       => 0.299999999999999988897769753748...

差は正確に2である^-54〜5.5511151231258×10であり、^-17 - （多くの用途のために）有意でない元の値と比較した場合。

有名な「すべてのコンピューター科学者が浮動小数点演算について知っておくべきこと」（この回答のすべての主要部分をカバーしている）を読む人なら誰でも知っているので、浮動小数点数の最後の数ビットを比較することは本質的に危険です。

ほとんどの電卓は、追加の使用保護桁をどのようにしている、この問題を回避するために0.1 + 0.2与えるだろう0.3。最後の数のビットが丸みを帯びています。

Answer 8

コンピューターに格納されている浮動小数点数は、整数と、底をとって整数部分を掛ける指数の2つの部分で構成されます。

コンピュータがベース10で作業していた場合、0.1だろう1 x 10⁻¹、0.2となり2 x 10⁻¹、そして0.3だろう3 x 10⁻¹。整数の計算は簡単で正確なので、追加0.1 + 0.2すると明らかに0.3。になります。

コンピュータは、ベース10でない通常の作業を行う、彼らは例えば、あなたはまだいくつかの値の正確な結果を得ることができますベース2での作業0.5である1 x 2⁻¹と0.25され1 x 2⁻²、それらを追加することになり3 x 2⁻²、または0.75。丁度。

問題は、基数10で正確に表すことができるが、基数2では表すことができない数値にあります。これらの数値は、最も近いものに丸める必要があります。非常に一般的なIEEE64ビット浮動小数点形式を想定すると、に最も近い数0.1は3602879701896397 x 2⁻⁵⁵、であり、に最も近い数0.2は7205759403792794 x 2⁻⁵⁵;です。それらを合計すると、、10808639105689191 x 2⁻⁵⁵または正確な10進値がになり0.3000000000000000444089209850062616169452667236328125ます。浮動小数点数は通常、表示のために丸められます。

Answer 9

浮動小数点の丸め誤差。すべてのコンピューター科学者が浮動小数点演算について知っておくべきことから：

無限に多くの実数を有限のビット数に圧縮するには、近似表現が必要です。整数は無限にありますが、ほとんどのプログラムでは、整数計算の結果を32ビットで格納できます。対照的に、ビット数が固定されている場合、実数を使用したほとんどの計算では、その数のビットを使用して正確に表すことができない量が生成されます。したがって、浮動小数点計算の結果は、有限表現に戻すために丸める必要があります。この丸め誤差は、浮動小数点計算の特徴です。

Answer 10

私の回避策：

function add(a, b, precision) {
    var x = Math.pow(10, precision || 2);
    return (Math.round(a * x) + Math.round(b * x)) / x;
}

精度とは、加算時に小数点以下を保持する桁数を指します。

Answer 11

良い回答がたくさん投稿されていますが、もう1つ追加したいと思います。

すべての数値をfloat / doubleで表すことができるわけではありません。たとえば、IEEE754浮動小数点標準では、数値「0.2」は単精度で「0.200000003」として表されます。

内部の実数を格納するためのモデルは、フロート数を次のように表します。

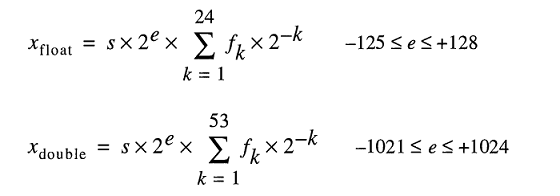
次のように入力することができたとしても0.2、容易、FLT_RADIXかつDBL_RADIX2です。「バイナリ浮動小数点演算のIEEE標準（ISO / IEEE Std 754-1985）」を使用するFPUを搭載したコンピュータの場合は10ではありません。

したがって、そのような数値を正確に表すのは少し難しいです。この変数を中間計算なしで明示的に指定した場合でも。

Answer 12

この有名な倍精度の質問に関連するいくつかの統計。

0.1のステップ（0.1から100）を使用してすべての値（a + b）を加算すると、精度エラーの確率は最大15％になります。エラーにより、値がわずかに大きくなったり小さくなったりする可能性があることに注意してください。ここではいくつかの例を示します。

0.1 + 0.2 = 0.30000000000000004 (BIGGER)
0.1 + 0.7 = 0.7999999999999999 (SMALLER)
...
1.7 + 1.9 = 3.5999999999999996 (SMALLER)
1.7 + 2.2 = 3.9000000000000004 (BIGGER)
...
3.2 + 3.6 = 6.800000000000001 (BIGGER)
3.2 + 4.4 = 7.6000000000000005 (BIGGER)

0.1のステップ（100から0.1）を使用してすべての値（a --b、ここでa> b）を減算すると、精度エラーの確率は約34％になります。ここではいくつかの例を示します。

0.6 - 0.2 = 0.39999999999999997 (SMALLER)
0.5 - 0.4 = 0.09999999999999998 (SMALLER)
...
2.1 - 0.2 = 1.9000000000000001 (BIGGER)
2.0 - 1.9 = 0.10000000000000009 (BIGGER)
...
100 - 99.9 = 0.09999999999999432 (SMALLER)
100 - 99.8 = 0.20000000000000284 (BIGGER)

* 15％と34％は確かに巨大なので、精度が非常に重要な場合は常にBigDecimalを使用してください。10進数の2桁（ステップ0.01）を使用すると、状況はもう少し悪化します（18％および36％）。

Answer 13

いいえ、壊れていませんが、ほとんどの小数は概算する必要があります

概要

浮動小数点演算は正確ですが、残念ながら、通常の10進数の表現とはよく一致しません。そのため、私たちが書いたものとは少し異なる入力を与えることがよくあります。

0.01、0.02、0.03、0.04 ... 0.24のような単純な数値でさえ、2進分数として正確に表すことはできません。0.01、.02、.03 ...を数えると、0.25に達するまで、基数_2で表現できる最初の分数が得られません。FPを使用して試してみた場合、0.01はわずかにずれていたため、25個を正確な0.25に追加する唯一の方法は、ガードビットと丸めを含む因果関係の長いチェーンを必要としたでしょう。予測するのは難しいので、手を挙げて「FPは不正確です」と言いますが、それは本当ではありません。

FPハードウェアには、基数10では単純に見えますが、基数2では繰り返し分数であるものを常に提供しています。

どうしてそうなった？

10進数で書く場合、すべての分数（具体的にはすべての終了小数）は次の形式の有理数です。

           a /（2 ⁿ x 5 ^m）

バイナリでは、2 ^nの項のみを取得します。つまり、次のようになります。

           a / 2 ⁿ

したがって、10進数では、¹ / _3を表すことはできません。ベース10は、素因数として2を含んでいるので、我々はバイナリ分数として記述することができ、すべての数はまた、ベース10分数のように記述することができます。ただし、基数_10の分数として記述したものは、バイナリで表現できるものはほとんどありません。0.01、0.02、0.03 ... 0.99の範囲では、FP形式で表すことができるのは0.25、0.50、0.75の3つの数値のみです。これらはすべて、1 / 4、1 / 2、および3/4であるためです。²ⁿ項のみを使用する素因数を使用します。

ベースで₁₀我々は表現できない¹ / ₃。しかし、バイナリでは、我々が行うことができない¹ / ₁₀ または ¹ / ₃。

したがって、すべての2進数の分数は10進数で記述できますが、その逆は当てはまりません。実際、ほとんどの小数は2進数で繰り返されます。

それに対処する

開発者は通常、<イプシロン比較を行うように指示されます。より良いアドバイスは、整数値に丸めて（Cライブラリではround（）とroundf（）、つまりFP形式のまま）比較することです。特定の小数部の長さに丸めると、出力に関するほとんどの問題が解決されます。

また、実数計算の問題（FPが初期の恐ろしく高価なコンピューターで発明された問題）では、宇宙の物理定数と他のすべての測定値は、比較的少数の有効数字しか知らないため、問題空間全体がわかります。とにかく「不正確」でした。この種のアプリケーションでは、FPの「精度」は問題ではありません。

人々が豆の数え方にFPを使おうとすると、全体の問題が実際に発生します。それはそのために機能しますが、それを使用するポイントを打ち負かすような整数値に固執する場合に限ります。これが、これらすべての小数部ソフトウェアライブラリがある理由です。

私はクリスによるピザの答えが大好きです。なぜなら、それは「不正確さ」についての通常の手振りだけでなく、実際の問題を説明しているからです。FPが単に「不正確」だったとしたら、それを修正することができ、数十年前にそれを行っていたでしょう。私たちがそうしなかった理由は、FP形式がコンパクトで高速であり、多くの数値を処理するための最良の方法だからです。また、それは宇宙時代と軍拡競争からの遺産であり、小さなメモリシステムを使用する非常に遅いコンピュータの大きな問題を解決するための初期の試みです。（1ビットストレージ用の個々の磁気コアもありますが、それは別の話です。）

結論

銀行でBeanを数えているだけの場合は、最初に10進文字列表現を使用するソフトウェアソリューションが完全に機能します。しかし、そのように量子色力学や空気力学を行うことはできません。

Answer 14

要するに、それは理由です：

浮動小数点数は、すべての小数を2進数で正確に表すことはできません

したがって、基数10に正確に存在しない3/10 （3.33 ...繰り返し）と同じように、1/10はバイナリに存在しません。

だから何？どのように対処しますか？回避策はありますか？

私が言うことができる最良の解決策を提供するために、私は次の方法を発見しました：

parseFloat((0.1 + 0.2).toFixed(10)) => Will return 0.3

それが最良の解決策である理由を説明しましょう。上記の回答で言及されているように、問題を解決するには、すぐに使用できるJavascript toFixed（）関数を使用することをお勧めします。しかし、ほとんどの場合、いくつかの問題が発生します。

あなたのような2つのfloatの数値を足ししようとしていると想像0.2して0.7：ここにあります0.2 + 0.7 = 0.8999999999999999。

期待される結果は0.9、この場合、1桁の精度の結果が必要であることを意味します。したがって、使用する必要(0.2 + 0.7).tofixed(1)がありますが、toFixed（）に特定のパラメーターを指定することはできません。これは、たとえば、指定された数に依存するためです。

0.22 + 0.7 = 0.9199999999999999

この例では、2桁の精度が必要なのでtoFixed(2)、そうする必要があります。したがって、指定されたすべての浮動小数点数に適合するパラメータは何でしょうか。

あなたはそれがすべての状況で10になると言うかもしれません：

(0.2 + 0.7).toFixed(10) => Result will be "0.9000000000"

くそー！9以降の不要なゼロをどうしますか？それはあなたが望むようにそれを作るためにそれをフロートに変換する時です：

parseFloat((0.2 + 0.7).toFixed(10)) => Result will be 0.9

解決策が見つかったので、次のような関数として提供することをお勧めします。

function floatify(number){
           return parseFloat((number).toFixed(10));
        }
    

自分で試してみましょう：

function floatify(number){
       return parseFloat((number).toFixed(10));
    }
 
function addUp(){
  var number1 = +$("#number1").val(); var number2 = +$("#number2").val();
  var unexpectedResult = number1 + number2;
  var expectedResult = floatify(number1 + number2);
  $("#unexpectedResult").text(unexpectedResult); $("#expectedResult").text(expectedResult);
}
addUp();

input{
  width: 50px;
}
#expectedResult{
color: green;
}
#unexpectedResult{
color: red;
}

<script src="https://ajax.googleapis.com/ajax/libs/jquery/2.1.1/jquery.min.js"></script>
<input id="number1" value="0.2" onclick="addUp()" onkeyup="addUp()"/> +
<input id="number2" value="0.7" onclick="addUp()" onkeyup="addUp()"/> =
<p>Expected Result: <span id="expectedResult"></span></p>
<p>Unexpected Result: <span id="unexpectedResult"></span></p>

次のように使用できます。

var x = 0.2 + 0.7;
floatify(x);  => Result: 0.9

以下のようW3Schoolsのは、別の解決策があまりにもそこにあることを示唆している、あなたは上記の問題を解決するために乗算と除算することができます：

var x = (0.2 * 10 + 0.1 * 10) / 10;       // x will be 0.3

(0.2 + 0.1) * 10 / 10同じように見えますが、まったく機能しないことに注意してください。入力フロートを正確な出力フロートに変換する関数として適用できるため、最初のソリューションを好みます。

Answer 15

ダクトテープソリューションを試しましたか？

エラーがいつ発生するかを判断し、短いifステートメントで修正してみてください。きれいではありませんが、問題によってはそれが唯一の解決策であり、これはその1つです。

 if( (n * 0.1) < 100.0 ) { return n * 0.1 - 0.000000000000001 ;}
                    else { return n * 0.1 + 0.000000000000001 ;}    

私はc＃の科学シミュレーションプロジェクトでも同じ問題を抱えていました。バタフライ効果を無視すると、大きな太ったドラゴンに変わり、a **であなたを噛むことになります。

Answer 16

これらの奇妙な数は、コンピューターが計算目的で2進数（基数2）の記数法を使用しているのに対し、10進数（基数10）を使用しているために表示されます。

2進数または10進数、あるいはその両方で正確に表すことができない分数の大部分があります。結果-切り上げられた（ただし正確な）数値の結果。

Answer 17

誰もこれについて言及していないことを考えると...

PythonやJavaなどの一部の高級言語には、バイナリ浮動小数点の制限を克服するためのツールが付属しています。例えば：

• PythonのdecimalモジュールとJavaのBigDecimalクラス。これらは、（2進表記ではなく）10進表記で内部的に数値を表します。どちらも精度が限られているため、エラーが発生しやすくなりますが、バイナリ浮動小数点演算で最も一般的な問題を解決します。

  小数はお金を扱うときにとてもいいです：10セントプラス20セントは常に正確に30セントです：

  >>> 0.1 + 0.2 == 0.3
  False
  >>> Decimal('0.1') + Decimal('0.2') == Decimal('0.3')
  True
  

  Pythonのdecimalモジュールは、IEEE標準854-1987に基づいています。

• PythonのfractionsモジュールとApacheCommonのBigFractionクラス。どちらも有理数を(numerator, denominator)ペアとして表し、10進浮動小数点演算よりも正確な結果が得られる場合があります。

これらのソリューションはどちらも完璧ではありませんが（特にパフォーマンスを確認する場合、または非常に高い精度が必要な場合）、バイナリ浮動小数点演算に関する多くの問題を解決します。

Answer 18

この質問の多数の重複の多くは、特定の数値に対する浮動小数点の丸めの影響について尋ねています。実際には、単にそれについて読むよりも、関心のある計算の正確な結果を見ることによって、それがどのように機能するかを理解する方が簡単です。一部の言語では、JavaでfloatまたはdoubleをBigDecimalに変換するなどの方法が提供されています。

これは言語に依存しない質問であるため、Decimal to Floating-PointConverterなどの言語に依存しないツールが必要です。

それを質問の数字に適用し、doubleとして扱います。

0.1は0.1000000000000000055511151231257827021181583404541015625に変換されます。

0.2は0.200000000000000011102230246251565404236316680908203125に変換されます。

0.3は0.299999999999999988897769753748434595763683319091796875に変換され、

0.30000000000000004は0.3000000000000000444089209850062616169452667236328125に変換されます。

最初の2つの数値を手動で、またはFull Precision Calculatorなどの10進計算機に追加すると、実際の入力の正確な合計が0.3000000000000000166533453693773481063544750213623046875であることがわかります。

0.3に相当する値に切り捨てられた場合、丸め誤差は0.0000000000000000277555756156289135105907917022705078125になります。0.30000000000000004に相当する値に切り上げると、丸め誤差0.0000000000000000277555756156289135105907917022705078125も発生します。四捨五入のタイブレーカーが適用されます。

浮動小数点コンバーターに戻ると、0.30000000000000004の生の16進数は3fd3333333333334であり、これは偶数桁で終わるため、正しい結果になります。

Answer 19

追加できますか。人々はいつもこれをコンピュータの問題だと思っていますが、手で数えると（基数10）、(1/3+1/3=2/3)=true0.333 ...を0.333 ...に追加する無限大がないと取得できません。(1/10+2/10)!==3/10基数の問題と同じです。2、0.333 + 0.333 = 0.666に切り捨て、おそらく0.667に丸めますが、これも技術的に不正確です。

三元で数えますが、3分の1は問題ではありません。おそらく、片手に15本の指があるレースでは、小数の計算が壊れた理由を尋ねられるでしょう...

Answer 20

デジタルコンピュータに実装できる種類の浮動小数点演算は、必然的に実数の近似とそれらの演算を使用します。（標準バージョンは50ページを超えるドキュメントで実行され、その正誤表とさらなる改良に対処するための委員会があります。）

この近似は、さまざまな種類の近似の混合であり、正確さからの逸脱の特定の方法のために、それぞれを無視するか、慎重に説明することができます。また、ハードウェアレベルとソフトウェアレベルの両方で、ほとんどの人が気づかないふりをしながら通り過ぎていく、いくつかの明白な例外的なケースも含まれます。

無限の精度が必要な場合（たとえば、多くの短いスタンドインの1つではなくπを使用）、代わりに記号数学プログラムを作成または使用する必要があります。

しかし、浮動小数点演算の値があいまいで、ロジックとエラーがすぐに蓄積される可能性があり、それを可能にする要件とテストを記述できるという考えに問題がなければ、コードは頻繁に何が含まれているのかを理解できます。あなたのFPU。

Answer 21

楽しみのために、標準C99の定義に従って、フロートの表現を試して、以下のコードを記述しました。

コードは、フロートのバイナリ表現を3つの別々のグループに出力します

SIGN EXPONENT FRACTION

その後、合計を出力します。十分な精度で合計すると、ハードウェアに実際に存在する値が表示されます。

したがって、を書き込むfloat x = 999...と、コンパイラは、関数xxによって出力される合計が指定された数yyと等しくなるように、関数によって出力されるビット表現にその数を変換します。

実際には、この合計は概算にすぎません。数値999,999,999の場合、コンパイラはフロートのビット表現に数値1,000,000,000を挿入します。

コードの後に​​、コンソールセッションをアタッチします。このセッションでは、コンパイラによって挿入された、ハードウェアに実際に存在する両方の定数（PIと999999999を除く）の項の合計を計算します。

#include <stdio.h>
#include <limits.h>

void
xx(float *x)
{
    unsigned char i = sizeof(*x)*CHAR_BIT-1;
    do {
        switch (i) {
        case 31:
             printf("sign:");
             break;
        case 30:
             printf("exponent:");
             break;
        case 23:
             printf("fraction:");
             break;

        }
        char b=(*(unsigned long long*)x&((unsigned long long)1<<i))!=0;
        printf("%d ", b);
    } while (i--);
    printf("\n");
}

void
yy(float a)
{
    int sign=!(*(unsigned long long*)&a&((unsigned long long)1<<31));
    int fraction = ((1<<23)-1)&(*(int*)&a);
    int exponent = (255&((*(int*)&a)>>23))-127;

    printf(sign?"positive" " ( 1+":"negative" " ( 1+");
    unsigned int i = 1<<22;
    unsigned int j = 1;
    do {
        char b=(fraction&i)!=0;
        b&&(printf("1/(%d) %c", 1<<j, (fraction&(i-1))?'+':')' ), 0);
    } while (j++, i>>=1);

    printf("*2^%d", exponent);
    printf("\n");
}

void
main()
{
    float x=-3.14;
    float y=999999999;
    printf("%lu\n", sizeof(x));
    xx(&x);
    xx(&y);
    yy(x);
    yy(y);
}

---

これは、ハードウェアに存在するfloatの実際の値を計算するコンソールセッションです。以前bcは、メインプログラムから出力された項の合計を出力していました。その合計をPythonreplまたは同様のものに挿入することもできます。

-- .../terra1/stub
@ qemacs f.c
-- .../terra1/stub
@ gcc f.c
-- .../terra1/stub
@ ./a.out
sign:1 exponent:1 0 0 0 0 0 0 fraction:0 1 0 0 1 0 0 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 1
sign:0 exponent:1 0 0 1 1 1 0 fraction:0 1 1 0 1 1 1 0 0 1 1 0 1 0 1 1 0 0 1 0 1 0 0 0
negative ( 1+1/(2) +1/(16) +1/(256) +1/(512) +1/(1024) +1/(2048) +1/(8192) +1/(32768) +1/(65536) +1/(131072) +1/(4194304) +1/(8388608) )*2^1
positive ( 1+1/(2) +1/(4) +1/(16) +1/(32) +1/(64) +1/(512) +1/(1024) +1/(4096) +1/(16384) +1/(32768) +1/(262144) +1/(1048576) )*2^29
-- .../terra1/stub
@ bc
scale=15
( 1+1/(2) +1/(4) +1/(16) +1/(32) +1/(64) +1/(512) +1/(1024) +1/(4096) +1/(16384) +1/(32768) +1/(262144) +1/(1048576) )*2^29
999999999.999999446351872

それでおしまい。999999999の値は実際には

999999999.999999446351872

bc-3.14も摂動していることを確認することもできます。にscale係数を設定することを忘れないでくださいbc。

表示される合計は、ハードウェア内部のものです。計算によって得られる値は、設定したスケールによって異なります。scale係数を15に設定しました。数学的には、無限の精度で、1,000,000,000のようです。

Answer 22

これを見る別の方法：数値を表すために64ビットが使用されます。結果として、2 ** 64 = 18,446,744,073,709,551,616を超える異なる数値を正確に表すことはできません。

ただし、Mathによると、0から1までの小数点以下の桁数はすでに無限にあります。IEE754は、これらの64ビットをはるかに大きな数値スペースにNaNと+/-無限大を加えたものに効率的に使用するエンコーディングを定義しているため、数値は概算です。

残念ながら、0.3はギャップにあります。

Answer 23

Python 3.5以降、math.isclose()関数を使用して近似等式をテストできます。

>>> import math
>>> math.isclose(0.1 + 0.2, 0.3)
True
>>> 0.1 + 0.2 == 0.3
False

Answer 24

たとえば、8桁の精度で基数10で作業することを想像してみてください。あなたは

1/3 + 2 / 3 == 1

そして、これがを返すことを学びますfalse。どうして？まあ、実数として私たちは持っています

1/3 = 0.333 ....および2/3 = 0.666...。

小数点以下8桁で切り捨てると、次のようになります。

0.33333333 + 0.66666666 = 0.99999999

もちろん、これは1.00000000正確にとは異なり0.00000001ます。

---

ビット数が固定されている2進数の状況は、まったく同じです。実数として、

1/10 = 0.0001100110011001100 ...（基数2）

そして

1/5 = 0.0011001100110011001 ...（基数2）

これらをたとえば7ビットに切り捨てると、次のようになります。

0.0001100 + 0.0011001 = 0.0100101

一方、

3/10 = 0.01001100110011 ...（基数2）

これは、7ビットに切り捨てられ、であり0.0100110、これらは正確に異なります0.0000001。

---

これらの数値は通常、科学的記数法で保存されるため、正確な状況は少し微妙です。したがって、たとえば、指数と仮数に割り当てたビット数に応じて、1/10を格納する代わりに、の0.0001100ようなものとして格納する場合があります1.10011 * 2^-4。これは、計算で得られる精度の桁数に影響します。

結果として、これらの丸め誤差のために、浮動小数点数で==を使用することは基本的に望ましくありません。代わりに、それらの差の絶対値がいくつかの固定された小さい数よりも小さいかどうかを確認できます。

Answer 25

小数のような番号0.1、0.2および0.3バイナリ形式で正確に表現されていない浮動小数点型をコードしていました。の近似値の合計は、に使用される近似値0.1と0.2は異なります0.3。したがって、0.1 + 0.2 == 0.3asの虚偽は、ここでより明確に確認できます。

#include <stdio.h>

int main() {
    printf("0.1 + 0.2 == 0.3 is %s\n", 0.1 + 0.2 == 0.3 ? "true" : "false");
    printf("0.1 is %.23f\n", 0.1);
    printf("0.2 is %.23f\n", 0.2);
    printf("0.1 + 0.2 is %.23f\n", 0.1 + 0.2);
    printf("0.3 is %.23f\n", 0.3);
    printf("0.3 - (0.1 + 0.2) is %g\n", 0.3 - (0.1 + 0.2));
    return 0;
}

出力：

0.1 + 0.2 == 0.3 is false
0.1 is 0.10000000000000000555112
0.2 is 0.20000000000000001110223
0.1 + 0.2 is 0.30000000000000004440892
0.3 is 0.29999999999999998889777
0.3 - (0.1 + 0.2) is -5.55112e-17

これらの計算をより確実に評価するには、浮動小数点値に10進数ベースの表現を使用する必要があります。C標準では、このようなタイプはデフォルトでは指定されていませんが、テクニカルレポートに記載されている拡張機能として指定されています。

_Decimal32、_Decimal64および_Decimal128タイプがシステム上で利用可能であるかもしれない（例えば、GCCは、上でそれらをサポートして選択したターゲットが、クランは上でそれらをサポートしていないOS X）。

Answer 26

このスレッドは、現在の浮動小数点の実装に関する一般的な議論に少し分岐したので、それらの問題を修正するプロジェクトがあることを付け加えておきます。

Take a look at https://posithub.org/ for example, which showcases a number type called posit (and its predecessor unum) that promises to offer better accuracy with fewer bits. If my understanding is correct, it also fixes the kind of problems in the question. Quite interesting project, the person behind it is a mathematician it Dr. John Gustafson. The whole thing is open source, with many actual implementations in C/C++, Python, Julia and C# (https://hastlayer.com/arithmetics).

Answer 27

It's actually pretty simple. When you have a base 10 system (like ours), it can only express fractions that use a prime factor of the base. The prime factors of 10 are 2 and 5. So 1/2, 1/4, 1/5, 1/8, and 1/10 can all be expressed cleanly because the denominators all use prime factors of 10. In contrast, 1/3, 1/6, and 1/7 are all repeating decimals because their denominators use a prime factor of 3 or 7. In binary (or base 2), the only prime factor is 2. So you can only express fractions cleanly which only contain 2 as a prime factor. In binary, 1/2, 1/4, 1/8 would all be expressed cleanly as decimals. While, 1/5 or 1/10 would be repeating decimals. So 0.1 and 0.2 (1/10 and 1/5) while clean decimals in a base 10 system, are repeating decimals in the base 2 system the computer is operating in. When you do math on these repeating decimals, you end up with leftovers which carry over when you convert the computer's base 2 (binary) number into a more human readable base 10 number.

From https://0.30000000000000004.com/

Answer 28

Normal arithmetic is base-10, so decimals represent tenths, hundredths, etc. When you try to represent a floating-point number in binary base-2 arithmetic, you are dealing with halves, fourths, eighths, etc.

In the hardware, floating points are stored as integer mantissas and exponents. Mantissa represents the significant digits. Exponent is like scientific notation but it uses a base of 2 instead of 10. For example 64.0 would be represented with a mantissa of 1 and exponent of 6. 0.125 would be represented with a mantissa of 1 and an exponent of -3.

Floating point decimals have to add up negative powers of 2

0.1b = 0.5d
0.01b = 0.25d
0.001b = 0.125d
0.0001b = 0.0625d
0.00001b = 0.03125d

and so on.

It is common to use a error delta instead of using equality operators when dealing with floating point arithmetic. Instead of

if(a==b) ...

you would use

delta = 0.0001; // or some arbitrarily small amount
if(a - b > -delta && a - b < delta) ...

Answer 29

Floating point numbers are represented, at the hardware level, as fractions of binary numbers (base 2). For example, the decimal fraction:

0.125

has the value 1/10 + 2/100 + 5/1000 and, in the same way, the binary fraction:

0.001

has the value 0/2 + 0/4 + 1/8. These two fractions have the same value, the only difference is that the first is a decimal fraction, the second is a binary fraction.

Unfortunately, most decimal fractions cannot have exact representation in binary fractions. Therefore, in general, the floating point numbers you give are only approximated to binary fractions to be stored in the machine.

The problem is easier to approach in base 10. Take for example, the fraction 1/3. You can approximate it to a decimal fraction:

0.3

or better,

0.33

or better,

0.333

etc. No matter how many decimal places you write, the result is never exactly 1/3, but it is an estimate that always comes closer.

Likewise, no matter how many base 2 decimal places you use, the decimal value 0.1 cannot be represented exactly as a binary fraction. In base 2, 1/10 is the following periodic number:

0.0001100110011001100110011001100110011001100110011 ...

Stop at any finite amount of bits, and you'll get an approximation.

For Python, on a typical machine, 53 bits are used for the precision of a float, so the value stored when you enter the decimal 0.1 is the binary fraction.

0.00011001100110011001100110011001100110011001100110011010

which is close, but not exactly equal, to 1/10.

It's easy to forget that the stored value is an approximation of the original decimal fraction, due to the way floats are displayed in the interpreter. Python only displays a decimal approximation of the value stored in binary. If Python were to output the true decimal value of the binary approximation stored for 0.1, it would output:

>>> 0.1
0.1000000000000000055511151231257827021181583404541015625

This is a lot more decimal places than most people would expect, so Python displays a rounded value to improve readability:

>>> 0.1
0.1

It is important to understand that in reality this is an illusion: the stored value is not exactly 1/10, it is simply on the display that the stored value is rounded. This becomes evident as soon as you perform arithmetic operations with these values:

>>> 0.1 + 0.2
0.30000000000000004

This behavior is inherent to the very nature of the machine's floating-point representation: it is not a bug in Python, nor is it a bug in your code. You can observe the same type of behavior in all other languages ​​that use hardware support for calculating floating point numbers (although some languages ​​do not make the difference visible by default, or not in all display modes).

Another surprise is inherent in this one. For example, if you try to round the value 2.675 to two decimal places, you will get

>>> round (2.675, 2)
2.67

The documentation for the round() primitive indicates that it rounds to the nearest value away from zero. Since the decimal fraction is exactly halfway between 2.67 and 2.68, you should expect to get (a binary approximation of) 2.68. This is not the case, however, because when the decimal fraction 2.675 is converted to a float, it is stored by an approximation whose exact value is :

2.67499999999999982236431605997495353221893310546875

Since the approximation is slightly closer to 2.67 than 2.68, the rounding is down.

If you are in a situation where rounding decimal numbers halfway down matters, you should use the decimal module. By the way, the decimal module also provides a convenient way to "see" the exact value stored for any float.

>>> from decimal import Decimal
>>> Decimal (2.675)
>>> Decimal ('2.67499999999999982236431605997495353221893310546875')

Another consequence of the fact that 0.1 is not exactly stored in 1/10 is that the sum of ten values ​​of 0.1 does not give 1.0 either:

>>> sum = 0.0
>>> for i in range (10):
... sum + = 0.1
...>>> sum
0.9999999999999999

The arithmetic of binary floating point numbers holds many such surprises. The problem with "0.1" is explained in detail below, in the section "Representation errors". See The Perils of Floating Point for a more complete list of such surprises.

It is true that there is no simple answer, however do not be overly suspicious of floating virtula numbers! Errors, in Python, in floating-point number operations are due to the underlying hardware, and on most machines are no more than 1 in 2 ** 53 per operation. This is more than necessary for most tasks, but you should keep in mind that these are not decimal operations, and every operation on floating point numbers may suffer from a new error.

Although pathological cases exist, for most common use cases you will get the expected result at the end by simply rounding up to the number of decimal places you want on the display. For fine control over how floats are displayed, see String Formatting Syntax for the formatting specifications of the str.format () method.

This part of the answer explains in detail the example of "0.1" and shows how you can perform an exact analysis of this type of case on your own. We assume that you are familiar with the binary representation of floating point numbers.The term Representation error means that most decimal fractions cannot be represented exactly in binary. This is the main reason why Python (or Perl, C, C ++, Java, Fortran, and many others) usually doesn't display the exact result in decimal:

>>> 0.1 + 0.2
0.30000000000000004

Why ? 1/10 and 2/10 are not representable exactly in binary fractions. However, all machines today (July 2010) follow the IEEE-754 standard for the arithmetic of floating point numbers. and most platforms use an "IEEE-754 double precision" to represent Python floats. Double precision IEEE-754 uses 53 bits of precision, so on reading the computer tries to convert 0.1 to the nearest fraction of the form J / 2 ** N with J an integer of exactly 53 bits. Rewrite :

1/10 ~ = J / (2 ** N)

in :

J ~ = 2 ** N / 10

remembering that J is exactly 53 bits (so> = 2 ** 52 but <2 ** 53), the best possible value for N is 56:

>>> 2 ** 52
4503599627370496
>>> 2 ** 53
9007199254740992
>>> 2 ** 56/10
7205759403792793

So 56 is the only possible value for N which leaves exactly 53 bits for J. The best possible value for J is therefore this quotient, rounded:

>>> q, r = divmod (2 ** 56, 10)
>>> r
6

Since the carry is greater than half of 10, the best approximation is obtained by rounding up:

>>> q + 1
7205759403792794

Therefore the best possible approximation for 1/10 in "IEEE-754 double precision" is this above 2 ** 56, that is:

7205759403792794/72057594037927936

Note that since the rounding was done upward, the result is actually slightly greater than 1/10; if we hadn't rounded up, the quotient would have been slightly less than 1/10. But in no case is it exactly 1/10!

So the computer never "sees" 1/10: what it sees is the exact fraction given above, the best approximation using the double precision floating point numbers from the "" IEEE-754 ":

>>>. 1 * 2 ** 56
7205759403792794.0

If we multiply this fraction by 10 ** 30, we can observe the values ​​of its 30 decimal places of strong weight.

>>> 7205759403792794 * 10 ** 30 // 2 ** 56
100000000000000005551115123125L

meaning that the exact value stored in the computer is approximately equal to the decimal value 0.100000000000000005551115123125. In versions prior to Python 2.7 and Python 3.1, Python rounded these values ​​to 17 significant decimal places, displaying “0.10000000000000001”. In current versions of Python, the displayed value is the value whose fraction is as short as possible while giving exactly the same representation when converted back to binary, simply displaying “0.1”.

Answer 30

I just saw this interesting issue around floating points:

Consider the following results:

error = (2**53+1) - int(float(2**53+1))

>>> (2**53+1) - int(float(2**53+1))
1

We can clearly see a breakpoint when 2**53+1 - all works fine until 2**53.

>>> (2**53) - int(float(2**53))
0

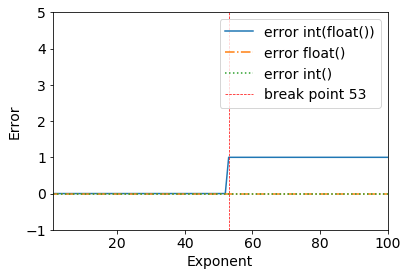
This happens because of the double-precision binary: IEEE 754 double-precision binary floating-point format: binary64

From the Wikipedia page for Double-precision floating-point format:

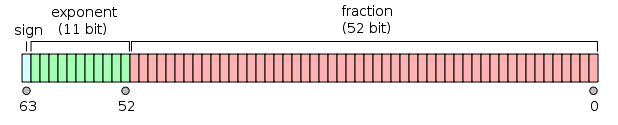
Double-precision binary floating-point is a commonly used format on PCs, due to its wider range over single-precision floating point, in spite of its performance and bandwidth cost. As with single-precision floating-point format, it lacks precision on integer numbers when compared with an integer format of the same size. It is commonly known simply as double. The IEEE 754 standard specifies a binary64 as having:

• Sign bit: 1 bit
• Exponent: 11 bits
• Significant precision: 53 bits (52 explicitly stored)

The real value assumed by a given 64-bit double-precision datum with a given biased exponent and a 52-bit fraction is

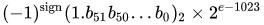
or

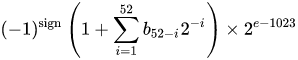
Thanks to @a_guest for pointing that out to me.