ウィルソン効果:黒点はどのくらい「深い」ですか?
私は最近、太陽の大気のウィルソン効果について学びました。2009サースフェー上級コース39の状態:
太陽黒点の近くでは、黒点[黒点の円形の暗い領域]と中央側の半影[黒点の明るい境界]が消えます。私たちは見る$400-800{\rm km}$ 光球よりも黒点の奥深くに。
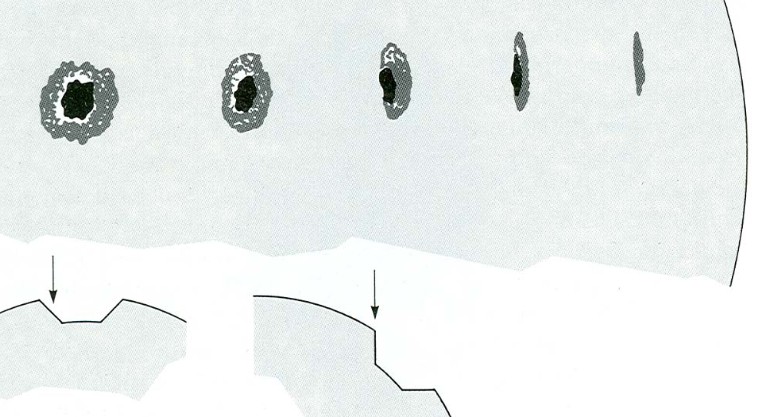
次に、「太陽黒点-浅いですか、深いですか?」というタイトルの出版物があります。要約で言う2014年からのSolov'evとKirichekによる:
2つの黒点モデルが比較されます-浅いものと深いものです。前者によれば、黒点は、強い規則的な場と比較的冷たいプラズマによって占められている領域として、約4Mmの浅い深さまで太陽対流層に浸透します。[...]
さらに、2015年のBenjamin Beeckによる博士論文があります。これは、たとえば次のグラフを示しています。
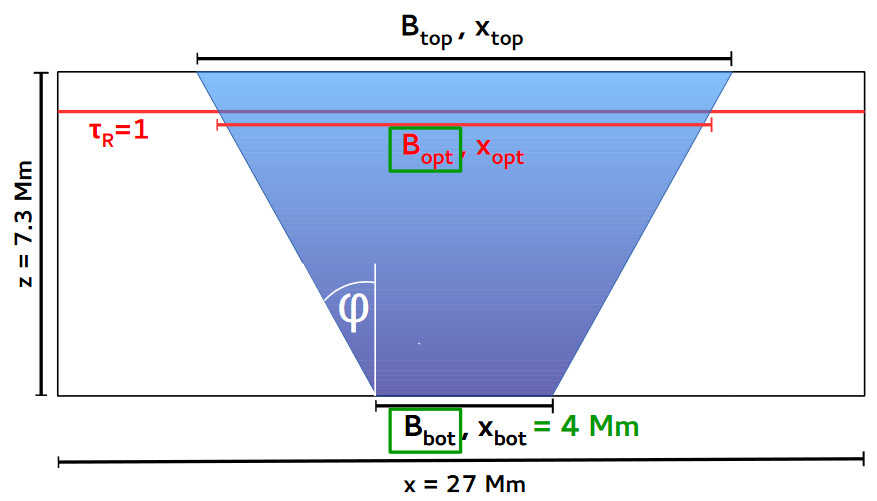
言い換えれば、私は間の値を持っています $400 \ldots 7300 {\rm km}=7.3 {\rm Mm}$私を少し混乱させる黒点の深さのために-誰かが私にかなり広い範囲の深さを説明してくれれば幸いです。一方では、半影から測定された傘の深さに興味があり(平らに見える場合)、他方では、半影から(の端までの距離も知りたい)目に見える)光球、理想的にはエラーバー付きのすべて。
回答
面白い質問!私は彼らに日光を当てることができるといいのですが。
あなたが引用している要約で述べられているように、黒点の理解とモデリングは未解決の問題であり、特に黒点の安定性がどのように維持されるかという問題です。
あなたの引用が示すように、多くのモデルがあります。まず、いくつかの用語の明確化:今日の「ウィルソン効果」は本質的に黒点の物理学を説明するためのモデルです。「ウィルソンくぼみ」は黒点の観測可能な要素です。目に見える太陽表面の幾何学的な高さは、太陽の他の部分と比較してくぼんでいます。ウィルソンの時、それは仮説でした、しかしそのようなうつ病は測定されました、例えば、ここの図を見てください。原則として、太陽黒点は光球の下の対流活動によって生成されるという考えであるため(つまり、対流熱輸送は強い磁場によってブロックされるため、安定した太陽黒点を維持するには強い磁場が必要です)、太陽黒点は次のようになります。光球の真下を見ることができないため(太陽のプラズマが不透明になりすぎるため)、私たちが観察できるものよりもはるかに深くなっています。
黒点の落ち込みを説明する他のモデルがあります。たとえば、最近のモデルは、モデルに依存する仮定がないために(明らかに)体系的な不確実性がなく、分光偏光観測から得られる磁場の発散を最小限に抑えています。黒点の観測に彼らの枠組みを適用することによって、彼らは次のように述べています。
導出されたウィルソン陥没(約600 km)は、ウィルソン効果から通常得られる結果と一致しています。
それらの結果は、たとえば、2009年のサースフェー上級コース39から引用したように、ウィルソン効果を採用した研究の結果と一致しています。
だから、あなたの質問:
誰かが私にかなり広い範囲の深さを説明してくれれば幸いです。半影から測定した陰影の深さ(平らに見える場合)に興味がある一方で、半影から(の端までの距離)も知りたいです。目に見える)光球、理想的にはエラーバー付きのすべて。
より正確な答えとエラーバーを備えたプロットを作成するには、誰かがすでにそのようなプロットを作成しているか、私が作成する必要があります。自分でそうする時間がなく、出版された論文を見つけることができません(そこにある可能性があります)。それで、もっと概念的に説明しようと思います。また、光球の下を見ることができないので、私が見つけるのに苦労している(そしてそれがまだ行われているかどうか疑問に思っている)傘の深さの観測でエラーバーを取得するために間接的な方法を使用する必要があると思います!編集:非常に参照してください日震学についての最後のパラグラフ)。
ウィキ記事は述べて:「うつ病の大きさが決定することは困難であるが、千キロ限り大きくなることがあります。」しかし、それはこの主張を引用していません;)
あなたが引用しているようなウィルソン効果のモデルは、太陽黒点の出現を恒星内部の対流層内から発生していると説明しようとしています。それは合理的ですか?:引用された深さ$\sim 7.3$これらのプラズマのうねりのMmは、少なくとも太陽半径内にあります。 $\sim 10^9$m = 1グラム。光球は、私たちが光学的に見ることができる太陽の内部の最も深いところにあり、それは約4x10まで伸びています。$^5$NS。したがって、黒点の底が深すぎることなく、太陽黒点が太陽の対流領域内の光球の下の深さに存在する可能性があると考えられます。
追加編集:Solov'evとKirichekのモデル、たとえば2014年では、「黒点の安定性は、半径と磁場強度の関数であり、半径が約700Gから約の漸近限界まで単調に変化します。 4000 G.ウィルソンくぼみの深さはBとともに直線的に増加します。安定した平衡の範囲は、より大きな黒点(半径が約12〜18 Mmより大きい)が不安定になるように制限されます。これは、上に非常に大きな黒点がないことを説明している可能性があります。太陽と、それらをいくつかの部分に分割する大きな黒点の光橋の外観。Bが2.6〜2.7 kGの範囲で、半径が約2Mmの黒点が最も安定しています。」この注4から引用 日震学のレビュー(以下の最後のパラグラフにもあります)。モデルの概略図については、そのレビューの図22を参照してください。
ここにある主要な記事であるB.Beeckが引用した論文では、影(または半影)の形状は事前にわかっていないため、推測を行い、詳細な数値シミュレーションで確認します。それらは、初期条件、境界条件、磁場強度、および黒点の深さを体系的に変化させて、物理的に安定した黒点を生成しようとします。彼らは見つけます:
安定した黒点は、地下層に4kGを超える磁場を必要とします。z〜2-3 Mm以下の構造(例えばT勾配)は黒点の安定性にとって重要であるように思われます。これはまた、黒点が非常に浅い現象であってはならないことを示しています。したがって、彼らは次のように結論付けています。安定した黒点には、5〜6Mmの深さでB≥6kGの磁場が必要です。
彼らは、この安定性の要件が、平らな(つまり、深くない)黒点の形状を除外する可能性があると推測しています。彼らはこれをくさび/スラブの形状で定量化しようとします。黒点の下部の磁場強度が高いほど、黒点の強度が低くなり、半影がよりはっきりします(最後から5番目のスライドを参照)。黒点の形状。
追加編集:したがって、ここに含まれるスケールの範囲は、活発な研究分野の一部です。黒点が深くて大きく、〜Mmのオーダーであると疑う理論的な理由はたくさんありますが、太陽を調べることができるのは非常に深いので、通常は〜のオーダーでしか見ることができません。$10^5$m、これは光球の深さと一致しています。これにより、現在、アンブラとペナンブラの正確な構造と深さが十分に理解されていませんが、特定のフレームワーク内ではさまざまなパラメータへの依存が十分に理解されています。
この回答を投稿した直後、日震学は光球よりも深く探査するという問題を回避しようとする方法であり、有望であることに気づきました。日震学の進歩は、太陽の内部への洞察を長い間期待してきました。たとえば、こことここでは、黒点の深さについて同等の推定値が得られています。$\sim$1mm これは活発な研究分野であり、その発展を追うのは良いことだと思います。(半)最近のレビューについては、こちらをご覧ください。