Effetto Wilson: quanto sono "profonde" le macchie solari?
Di recente ho appreso dell'effetto Wilson dell'atmosfera solare. Il 2009 Saas Fee Advanced Course 39 afferma:
Vicino al lembo solare, l'ombra [la regione scura circolare di una macchia solare] e la penombra laterale centrale [il bordo più chiaro della macchia solare] scompaiono. Vediamo$400-800{\rm km}$ più profonde nelle macchie solari che nella fotosfera.
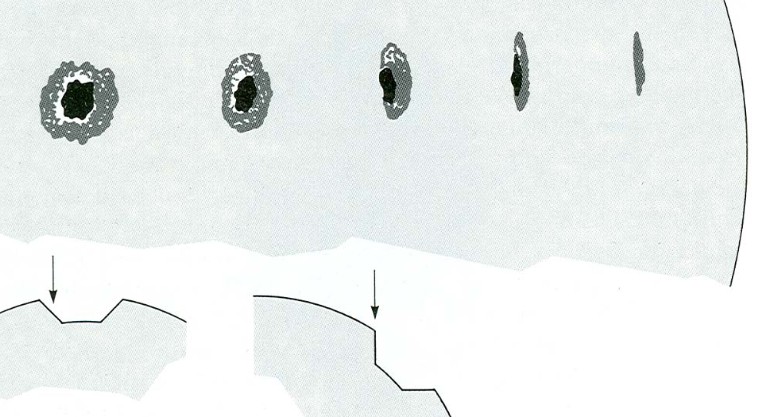
Poi c'è una pubblicazione intitolata La macchia solare: superficiale o profonda? di Solov'ev e Kirichek del 2014 che dice in astratto:
Vengono confrontati due modelli di macchie solari: superficiale e profonda. Secondo il primo, una macchia solare, come una regione occupata da un forte campo regolare e plasma relativamente freddo, penetra nella zona di convezione solare ad una profondità di circa 4 mm. [...]
Inoltre, esiste una tesi di dottorato di Benjamin Beeck del 2015 che mostra ad esempio il seguente grafico:
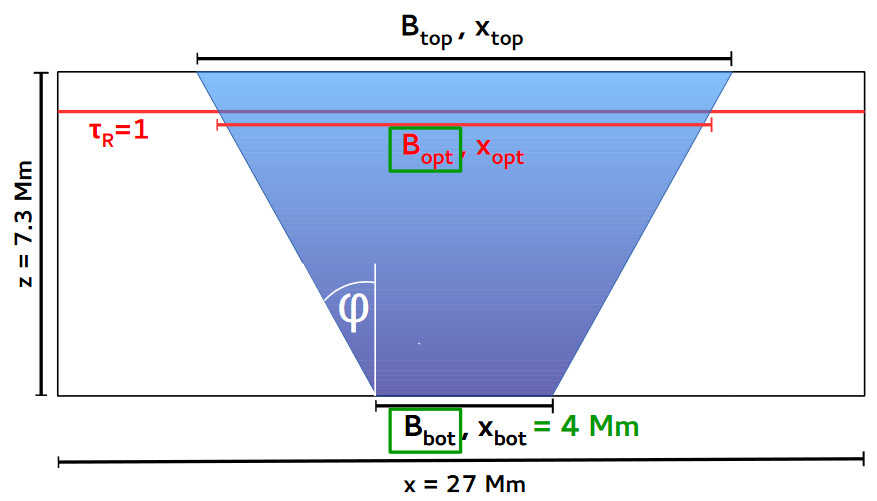
In altre parole, ho valori tra $400 \ldots 7300 {\rm km}=7.3 {\rm Mm}$per le profondità di una macchia solare che mi confonde leggermente - sarei grato se qualcuno potesse spiegarmi la gamma piuttosto ampia di profondità. Da una parte mi interessa la profondità dell'ombra misurata dalla penombra (se può essere vista piatta), e dall'altra vorrei anche conoscere la distanza dalla penombra alla fine del ( visibile) fotosfera, tutto idealmente con barre di errore.
Risposte
Domande interessanti! Spero di poterle illuminare con un po' di sole.
Come affermato nell'abstract che citi, la comprensione e la modellazione delle macchie solari è una questione aperta , in particolare la domanda su come viene sostenuta la stabilità delle macchie solari.
Ci sono molti modelli, come indicano le tue citazioni. Innanzitutto una precisazione terminologica: l'"effetto Wilson" oggi è essenzialmente un modello per spiegare la fisica della macchia solare. La "depressione di Wilson" è una componente osservabile di una macchia solare: l'altezza geometrica della superficie solare visibile è depressa rispetto al resto del Sole. Al tempo di Wilson, era un'ipotesi, ma tali depressioni sono state misurate, ad esempio, vedi la figura qui. In linea di principio, poiché l'idea è che la macchia solare sia generata dall'attività convettiva al di sotto della fotosfera (cioè, il trasporto di calore convettivo è bloccato da intensi campi magnetici, motivo per cui sono necessari forti campi magnetici per sostenere una macchia solare stabile), la macchia solare potrebbe essere molto più profondo di quello che siamo in grado di osservare, poiché non possiamo vedere direttamente sotto la fotosfera (poiché il plasma del Sole diventa troppo opaco).
Esistono altri modelli per spiegare la depressione di una macchia solare. Ad esempio, un modello recente , che è (apparentemente) privo di incertezze sistematiche dovute ad assunzioni non dipendenti dal modello, minimizza la divergenza del campo magnetico derivato dalle osservazioni spettropolarimetriche. Applicando la loro struttura alle osservazioni di una macchia solare, affermano:
La depressione di Wilson derivata (∼600 km) è coerente con i risultati tipicamente ottenuti dall'effetto Wilson.
I loro risultati sono coerenti con quelli di studi che impiegano l'effetto Wilson, ad esempio, come citi dal Saas Fee Advanced Course 39 del 2009.
Allora, le tue domande:
Apprezzerei se qualcuno potesse spiegarmi la gamma piuttosto ampia di profondità. Da un lato mi interessa la profondità dell'ombra misurata dalla penombra (se può essere vista piatta), e dall'altro vorrei anche conoscere la distanza dalla penombra alla fine del ( visibile) fotosfera, tutto idealmente con barre di errore.
Produrre una trama con risposte più precise e con barre di errore implicherebbe che qualcuno abbia già fatto una trama del genere, o dovrei farne una. Non ho tempo per farlo da solo, e non riesco a trovare un articolo pubblicato con esso (potrebbe essere là fuori). Quindi, cercherò di spiegare più concettualmente. Inoltre, non possiamo vedere sotto la fotosfera, quindi penso che dovrebbero essere usati metodi indiretti per ottenere barre di errore sulle osservazioni della profondità dell'ombra, che ho difficoltà a trovare (e dubito che sia stato ancora fatto! EDIT: vedi molto ultimo paragrafo sull'eliosismologia).
L' articolo della wiki afferma: "L'entità della depressione è difficile da determinare, ma può raggiungere i 1.000 km". Ma non cita questa affermazione ;)
I modelli dell'effetto Wilson, come quelli che citi, stanno tentando di spiegare l'emergere di una macchia solare come originata dall'interno dell'involucro convettivo dell'interno della stella. È ragionevole?: la profondità citata di$\sim 7.3$Mm per questi rigonfiamenti di plasma sono almeno all'interno del raggio solare, che è $\sim 10^9$m = 1 gr. La fotosfera è la più profonda all'interno del sole che possiamo vedere otticamente e si estende a circa 4x10$^5$m. Quindi è concepibile che la macchia solare possa esistere a profondità al di sotto della fotosfera all'interno di una regione convettiva del sole senza che il fondo della macchia solare sia troppo profondo.
EDIT AGGIUNTO: Nei modelli di Solov'ev e Kirichek, ad esempio, 2014, "la stabilità delle macchie solari [è] una funzione del loro raggio e dell'intensità del campo magnetico [che] varia in modo monotono con raggio da circa 700 G fino a un limite asintotico di circa 4000 G. La profondità della depressione di Wilson cresce linearmente con B. La gamma di equilibri stabili è limitata in modo tale che le macchie solari più grandi (raggio maggiore di circa 12-18 mm) sono instabili, il che può spiegare l'assenza di macchie solari molto grandi su il Sole, così come l'aspetto dei ponti di luce nelle grandi macchie solari che le dividono in più parti. Le macchie solari con B nell'intervallo 2,6-2,7 kG e un raggio d'ombra di circa 2 mm sono le più stabili." Citazione tratta dalla nota 4. di questo heliosismology review (anche nell'ultimo paragrafo sotto), e vedere la Figura 22 di quella review per uno schema del loro modello.
Nella tesi che citi di B. Beeck, l'articolo principale che trovi qui , la geometria dell'ombra (né della penombra) NON è nota a priori, quindi fanno ipotesi e verificano con le loro dettagliate simulazioni numeriche. Variano sistematicamente le condizioni iniziali, le condizioni al contorno, l'intensità del campo magnetico e la profondità della macchia solare per cercare di produrre una macchia solare fisicamente stabile. Loro trovano:
Le macchie solari stabili richiedono un campo magnetico > 4 kG negli strati del sottosuolo. La struttura (es. gradiente T) al di sotto di z~2-3 Mm sembra essere importante per la stabilità delle macchie solari. Ciò indica anche che le macchie solari non possono essere fenomeni molto superficiali. Quindi concludono: le macchie solari stabili necessitano di un campo magnetico di B ≥ 6 kG a una profondità di 5-6 mm.
Essi ipotizzano che questo requisito di stabilità possa escludere le geometrie delle macchie solari che sono piatte (cioè non profonde). Tentano di quantificare questo con la geometria del cuneo/lastra, dove una maggiore intensità del campo magnetico nella parte inferiore della macchia solare porta a una minore intensità dell'ombra e una penombra più pronunciata (vedi la quinta diapositiva dalla fine), che potrebbe essere utilizzata per escludere osservativamente alcuni geometrie di macchie solari.
EDIT AGGIUNTO: Pertanto, la gamma di scale qui coinvolte fa parte di un'area di ricerca attiva. Ci sono molte ragioni teoriche per sospettare che le macchie solari possano essere profonde e grandi, dell'ordine di ~Mm, ma possiamo sondare il sole solo così in profondità, quindi di solito siamo limitati a vedere solo nell'ordine di ~$10^5$m, che è coerente con la profondità della fotosfera. Ciò comporta che l'esatta struttura e profondità dell'ombra e della penombra non siano ben comprese, attualmente, sebbene la dipendenza da vari parametri sia ben compresa all'interno di determinati quadri.
Subito dopo aver pubblicato questa risposta, mi sono reso conto che l'eliosismologia è un modo per cercare di aggirare il problema del sondaggio più profondo della fotosfera e sembra promettente! I progressi nell'eliosismologia hanno anticipato da tempo intuizioni sull'interno del Sole, per esempi qui e qui , che ha prodotto stime comparabili per la profondità delle macchie solari, cioè$\sim$1 mm. Penso che questa sia un'area di ricerca attiva e sarà utile seguirne lo sviluppo. Vedi qui per una recensione (semi)recente.