Può l'albero Stern-Brocot essere impiegato per una migliore convergenza di $2^m/3^n$?
Prerequisiti di lettura:
- È possibile approssimare qualsiasi reale positivo come $2^m/3^n$ con $(m,n)$ abbastanza grande?
- Sequenza dell'albero di Stern Brocot
Motivo per cui ho cercato una procedura che non avesse questo inconveniente, ovvero dove l'approssimazione successiva è sempre più vicina al risultato desiderato. Questo è quello che ho provato finora.
Secondo la domanda (2.), per ogni numero reale positivo$0 \lt g \lt 1$, esiste una sequenza infinita nell'albero di Stern Brocot [..] che converge al numero reale. Nel frattempo, questa domanda ha una risposta e il risultato principale si legge come segue: $$ - \frac{1}{n_1(n_1+n_2)} \lt g - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} $$ In considerazione della domanda (1.), sostituiamo $\ln(2)/\ln(3)$ per quel numero $g$. Quindi ne consegue che: $$ - \frac{1}{n_1(n_1+n_2)} \lt \frac{\ln(2)}{\ln(3)} - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} \\ - \frac{\ln(3)}{n_1} \lt \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \lt + \frac{\ln(3)}{n_2} \\ \ln\left(3^{-1/n_1}\right) \lt \ln\left(\frac{2^{n_1+n_2}}{3^{m_1+m_2}}\right) \lt \ln\left(3^{+1/n_2}\right) \\ 3^{-1/n_1} \lt \frac{2^{n_1+n_2}}{3^{m_1+m_2}} \lt 3^{+1/n_2} $$La ricerca attraverso l'albero di Stern-Brocot può essere raffigurata. La linea blu è la funzione $\,\color{blue}{x\ln(2)-y\ln(3)=0}\,$, i piccoli cerchi sono frazioni, mappate su una griglia $\,m/n \to (m,n)\,$, punti pieni di nero massiccio sono le frazioni dell'albero Stern-Brocot. Si è visto che la ricerca attraverso l'albero è molto più efficiente che aumentare $m$ e $n$ con incrementi uno alla volta.
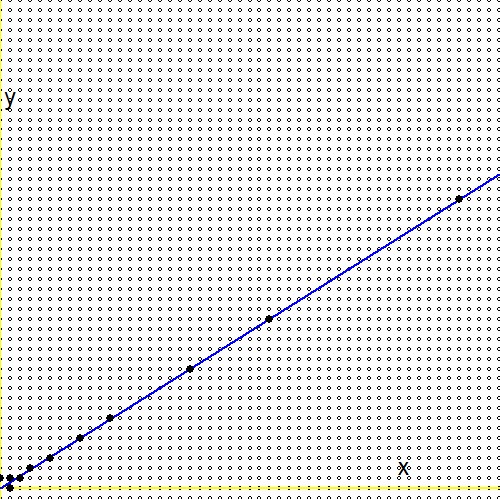
Ora confronta l'espressione alla seconda riga delle formule precedenti con un'espressione analoga nel riferimento (1.): $$ \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \quad \Longleftrightarrow \quad m\ln(2) - n\ln(3) - \ln(r) $$ E preparati a una delusione: il logaritmo del reale arbitrario $r$manca! Oppure in alternativa:$\ln(r)=0$ o $r=1$. Ciò significa che la nostra "ricerca infinita" attraverso l'albero di Stern-Brocot, sebbene altamente efficiente, arriva finalmente ad un'approssimazione solo per il numero uno. Lo trovo strano, perché - graficamente - non sembra esserci una grande differenza tra$\color{red}{2^m/3^n \to r}$ e $\color{blue}{2^m/3^n \to 1}$:
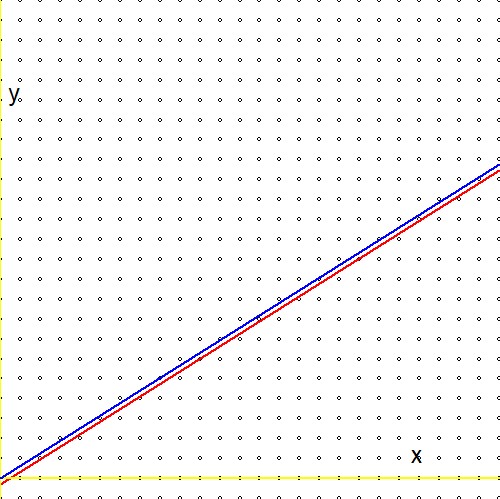
Da qui la DOMANDA: esiste un mezzo per adattare la procedura Stern-Brocot in modo tale che funzioni per reali diversi da uno?
MODIFICARE.
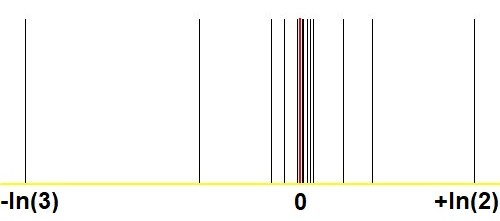
Ecco un altro grafico che mostra la sorprendente convergenza con il metodo Stern-Brocot, in confronto ad immagini analoghe nella mia domanda e risposta. È possibile approssimare qualsiasi reale positivo come$2^m/3^n$ con $(m,n)$abbastanza grande? :
Risposte
Darò un approccio che non utilizza la procedura Stern-Brocot.
Basta dimostrarlo $\frac{2^{m}}{3^{n}}$è denso nell'intervallo [1,2]. Da quando ho preso$\alpha\in (0,\infty)$ al di fuori di questo intervallo ce ne sono alcuni $k\in Z$ così che $\alpha = 2^{k}\gamma $ per alcuni $\gamma \in [1,2]$. Allora sappiamo che c'è una sequenza in$\frac{2^{m}}{3^{n}}$ che si avvicina $\gamma$, moltiplicando la sequenza a termine per $2^{k}$ (possibilmente prendendo una coda della sequenza), otteniamo una sequenza in $\frac{2^{m}}{3^{n}}$ che si avvicina $\alpha$.
Quindi considera che la mappa $f:[1,2] -> [0,1]$ con $f(x) = log_{2}(x)$ è una biiezione.
L'immagine di $\frac{2^{m}}{3^{n}}$ sotto la mappa è $N-Nlog_{2}(3)$. Quindi è sufficiente dimostrarlo$N-Nlog_{2}(3)$ è denso $[0,1]$.
Questa è una conseguenza del teorema di equidistribuzione di Weyl, che è un caso speciale del teorema ergodico.
Tenere conto $a=2-log_{2}(3) = log_{2}(\frac{4}{3})$, così $a$ è nell'immagine del set, Così è $na = log_{2}(\frac{4^{n}}{3^{n}})$ e così è la parte frazionaria di $na$.
Il teorema di equidistribuzione di Weyl (che non è un risultato banale) mostra che per a irrazionale la parte frazionaria di $na$è uniformemente distribuito e quindi denso su [0,1]. Da$2-log_{2}(3)$ è irrazionale puoi usare questo teorema.