Quanto dovrebbe essere grande un codice QR sul mio tetto perché un satellite sia in grado di scansionarlo data la risoluzione consentita oggi?
Dì, usando i satelliti di Planet Labs
Grazie
Risposte
Quanto dovrebbe essere grande un codice QR sul mio tetto perché un satellite sia in grado di scansionarlo data la risoluzione consentita oggi?
Dì, usando i satelliti di Planet Labs
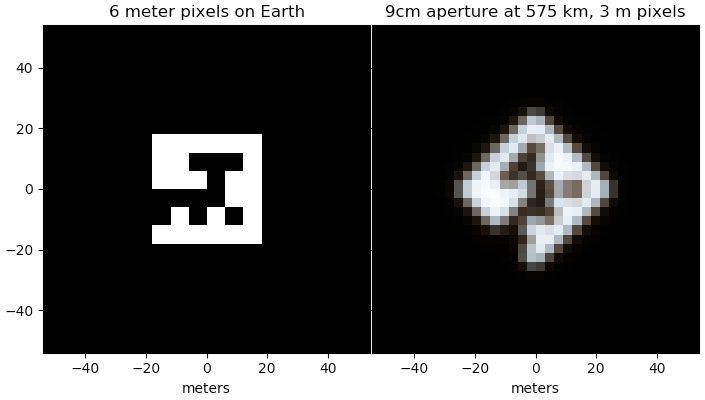
Questa è una risposta supplementare. Ho simulato pixel "QR" di 6 metri visti dallo spazio con un'apertura di 9 cm (dall'estremità di un cubo Dove 3U) a lunghezze d'onda di 450, 550 e 650 nm, ruotati di 45 gradi e quindi campionati con pixel di 3 metri.
È una sceneggiatura frammentaria e fragile, ma fa il suo lavoro.
L'immagine supporta la conclusione principale nell'altra risposta che questa è probabilmente la dimensione minima per una certa affidabilità di vederla con una colomba.
La sceneggiatura non è ottimale, ero pigro e ho usato PIL per ruotare, avrei potuto interpolare con scipy.ndimage.map_coordinates, e avrei potuto "fuzzificato" con scipy.ndimage.gaussian_filterinvece di un bel disco di Airy.
Le tonalità nell'immagine finale sono dovute ai limiti di diffrazione dell'apertura dipendenti dalla lunghezza d'onda, approssimativamente $1.22 \lambda / D$ variazione della risoluzione angolare con il rapporto tra lunghezza d'onda e apertura.
import numpy as np
import matplotlib.pyplot as plt
import itertools
from PIL import Image
from scipy import special as spe
from scipy.ndimage import convolve
N = 5*2
data = ('111111' + '110001' + '111011' +
'000011' + '010101' + '111111')
data = np.array([int(x) for x in data]).reshape((6, 6))
data = np.pad(data, ((6, 6), (6, 6)))
img = np.zeros((N*18, N*18, 3))
for i, j in itertools.product(np.arange(18), repeat=2):
img[N*i:N*(i+1), N*j:N*(j+1)] = data[i, j]
pixsize = 6 # meters
scale = pixsize/N
extent = 9*N * scale * np.array([-1, 1, -1, 1])
R = 575 * 1000. # meters distance
x = 4*N * scale * np.linspace(-1, 1, 8*N)
X, Y = np.meshgrid(x, x)
q = np.sqrt(X**2 + Y**2)
wavelengths = 1E-09 * np.array([650, 550, 450])
a = 0.045 # radius of aperture in meters (looking out end of a 3U cubesat)
x = (2 * np.pi * a / wavelengths) * (q[..., None] / R)
# https://en.wikipedia.org/wiki/Airy_disk
airy = (2 * spe.j1(x) / x)**2
areas = airy.sum(axis=0).sum(axis=0)
airy /= areas
new = [convolve(img[..., i], airy[..., i]) for i in range(3)]
newarray = np.stack(new, axis=2)
newarray = np.uint8(255 * newarray/newarray.max())
newimg = Image.fromarray(newarray)
newimg45 = newimg.rotate(45)
newimg45.show()
n45 = np.array(list(newimg45.getdata())).reshape(18*2, N>>1, 18*2, N>>1, 3)
n45 = np.uint8(n45.sum(axis=(1, 3)) / (N>>1)**2)
if True:
plt.figure()
plt.subplot(1, 2, 1)
plt.imshow(img, extent=extent)
plt.title('6 meter pixels on Earth')
plt.xlabel('meters')
plt.subplot(1, 2, 2)
plt.imshow(n45, extent=extent)
plt.title('9cm aperture at 575 km, 3 m pixels')
plt.xlabel('meters')
plt.show()
Quanto dovrebbe essere grande un codice QR sul mio tetto perché un satellite sia in grado di scansionarlo data la risoluzione consentita oggi?
Dì, usando i satelliti di Planet Labs
tl; dr: utilizzando 6x6 " tag di realtà aumentata " discusso nella risposta di @ CamilleGoudeseune come quella sul rover Curiosity e pixel di 6 metri (due volte la risoluzione minima per consentire traslazioni e rotazioni arbitrarie) il tuo modello dovrebbe essere di 36 x 36 metri per avere un buon cambiamento di essere avvistati e recuperati da un'immagine da una colomba PlanetLabs.
Rimuoverei la riflettività del rosso e dell'infrarosso dalle aree luminose e codificherei solo nelle lunghezze d'onda più corte, poiché le colombe hanno quattro canali di colore sono (probabilmente) limitati dalla diffrazione e lunghezze d'onda più lunghe potrebbero quindi avere una risoluzione peggiore.
Cerca di eccitare solo le bande di lunghezze d'onda più corte del tuo veicolo spaziale mirato per farle "apparire" agli spettatori occasionali, o guarda solo quelle lunghezze d'onda nel prodotto dati finale se stai cercando te stesso.
A https://www.planet.com/products/planet-imagery/i più numerosi satelliti o "Colombe" forniscono dati per il prodotto dati PLANETSCOPE. Si dice che i satelliti abbiano una risoluzione di 3,7 metri e il prodotto dati abbia una dimensione dei pixel ricampionata di 3 metri. Vedi anche la risposta di @ djr a Are these images from Planet Labs? Le immagini sono disponibili pubblicamente?
Se sei stato incredibilmente fortunato ad avere i pixel allineati con il tuo modello QR sia a livello di traslazione che di rotazione, potrebbero teoricamente essere di 3 metri.
In pratica, tuttavia, data la traduzione arbitraria e la rotazione del modello all'interno del campo dell'immagine, dovresti avere un fattore di almeno 2 se non 3 più grande di questo.
@Uwe ci ricorda che un piccolo codice QR sarebbe comunque abbastanza grande. Ci sono codici Micro QR 11 x 11 e gli spacefolks hanno utilizzato numeri di pixel ancora più piccoli per alternative ai codici QR con ancora meno pixel.
Per quelli vedi le risposte a:
- Perché Curiosity ha due immagini di se stessa o una è un codice QR?
- questa risposta a "QR" o altri codici a barre 2D sono stati utilizzati nei voli spaziali?


Gli stagisti di ingegneria Tristan Schuler, a sinistra, e Greta Studier posano con codici a barre 2D e un prototipo di Nano Air-Bearing Simulator che utilizza il sistema di navigazione sviluppato da Marshall. Il loro sistema di navigazione è disponibile come codice open source su code.nasa.gov. Crediti: NASA / Emmett Given