Effet Wilson : Quelle est la « profondeur » des taches solaires ?
J'ai récemment appris l' effet Wilson de l'atmosphère du Soleil. Le cours avancé Saas Fee 39 2009 stipule :
Près du limbe solaire, l'ombre [la région sombre circulaire d'une tache solaire] et la pénombre centrale [le bord plus clair de la tache solaire] disparaissent. Nous voyons$400-800{\rm km}$ plus profondément dans les taches solaires que dans la photosphère.
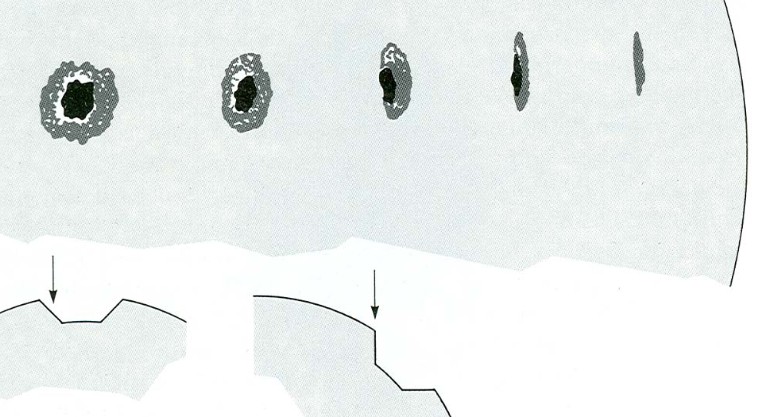
Ensuite, il y a une publication intitulée The sunspot—shallow or deep? par Solov'ev et Kirichek de 2014 qui dit dans l'abstrait :
Deux modèles de taches solaires sont comparés : peu profonds et profonds. Selon le premier, une tache solaire, en tant que région occupée par un champ régulier fort et un plasma relativement froid, pénètre dans la zone de convection solaire à une faible profondeur d'environ 4 mm. [...]
De plus, il existe une thèse de doctorat de Benjamin Beeck de 2015 qui montre par exemple le graphique suivant :
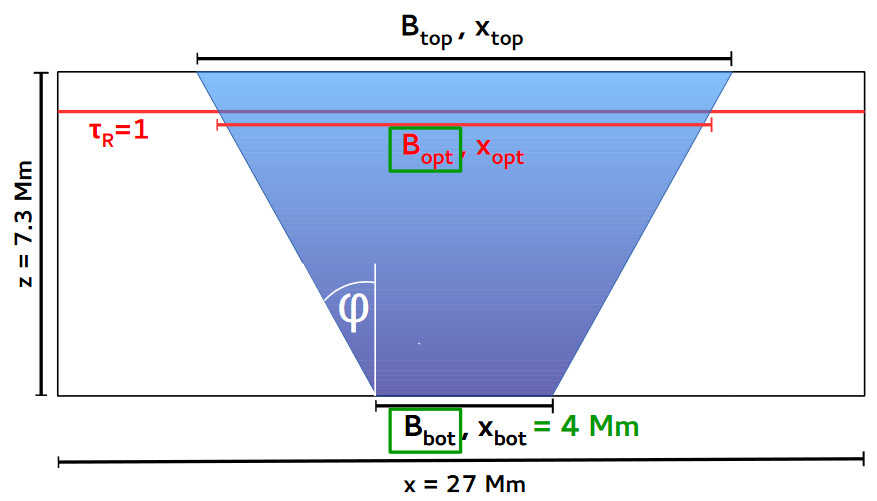
En d'autres termes, j'ai des valeurs entre $400 \ldots 7300 {\rm km}=7.3 {\rm Mm}$pour les profondeurs d'une tache solaire qui me trouble légèrement - j'apprécierais si quelqu'un pouvait m'expliquer la gamme assez large de profondeurs. D'une part, je m'intéresse à la profondeur de l'ombre mesurée à partir de la pénombre (si elle peut être vue comme plate), et d'autre part j'aimerais aussi connaître la distance de la pénombre à la fin de la ( visible) photosphère, le tout idéalement avec des barres d'erreur.
Réponses
Questions intéressantes ! J'espère pouvoir leur apporter un peu de soleil.
Comme indiqué dans le résumé que vous citez, la compréhension et la modélisation des taches solaires est une question ouverte , en particulier la question de savoir comment la stabilité des taches solaires est maintenue.
Il existe de nombreux modèles, comme vos citations l'indiquent. Tout d'abord, une clarification terminologique : l'« effet Wilson » est aujourd'hui essentiellement un modèle pour expliquer la physique de la tache solaire. La « dépression de Wilson » est une composante observable d'une tache solaire : la hauteur géométrique de la surface solaire visible est déprimée par rapport au reste du Soleil. A l'époque de Wilson, c'était une hypothèse, mais de telles dépressions ont été mesurées, par exemple, voir la figure ici. En principe, puisque l'idée est que la tache solaire est générée par l'activité convective sous la photosphère (c'est-à-dire que le transport de chaleur par convection est bloqué par des champs magnétiques intenses, c'est pourquoi des champs magnétiques puissants sont nécessaires pour maintenir une tache solaire stable), la tache solaire pourrait être beaucoup plus profond que ce que nous pouvons observer, car nous ne pouvons pas voir directement sous la photosphère (car le plasma du Soleil devient trop opaque).
Il existe d'autres modèles pour expliquer la dépression d'une tache solaire. Par exemple, un modèle récent , qui est (apparemment) exempt de toute incertitude systématique en raison de l'absence d'hypothèses dépendantes du modèle, minimise la divergence du champ magnétique dérivé des observations spectropolarimétriques. En appliquant leur cadre aux observations d'une tache solaire, ils déclarent :
La dépression de Wilson dérivée (∼600 km) est cohérente avec les résultats généralement obtenus à partir de l'effet Wilson.
Leurs résultats sont cohérents avec ceux des études qui utilisent l'effet Wilson, par exemple, comme vous le citez dans le Saas Fee Advanced Course 39 de 2009.
Alors, vos questions :
J'apprécierais si quelqu'un pouvait m'expliquer la gamme assez large de profondeurs. D'une part, je m'intéresse à la profondeur de l'ombre mesurée à partir de la pénombre (si elle peut être vue comme plate), et d'autre part j'aimerais aussi connaître la distance de la pénombre à la fin de la ( visible) photosphère, le tout idéalement avec des barres d'erreur.
Pour produire un tracé avec des réponses plus précises et avec des barres d'erreur, quelqu'un aurait déjà fait un tel tracé, ou je devrais en faire un. Je n'ai pas le temps de le faire moi-même et je ne trouve pas d'article publié avec (il pourrait être là-bas). Donc, je vais essayer d'expliquer plus conceptuellement. De plus, nous ne pouvons pas voir en dessous de la photosphère donc je pense qu'il faudrait utiliser des méthodes indirectes pour obtenir des barres d'erreur sur les observations de la profondeur de l'ombre, que j'ai du mal à trouver (et je doute que cela ait déjà été fait ! EDIT : voir le très dernier paragraphe sur l'héliosismologie).
L' article du wiki déclare : " L'ampleur de la dépression est difficile à déterminer, mais peut atteindre 1 000 km. " Mais il ne cite pas cette affirmation ;)
Des modèles de l'effet Wilson, comme ceux que vous citez, tentent d'expliquer l'émergence d'une tache solaire comme provenant de l'intérieur de l'enveloppe convective de l'intérieur stellaire. Est-ce raisonnable ? : la profondeur citée de$\sim 7.3$Mm pour ces houles de plasma sont au moins dans le rayon solaire, qui est $\sim 10^9$m = 1 Gm. La photosphère est la plus profonde à l'intérieur du soleil que nous puissions voir optiquement, et elle s'étend jusqu'à environ 4x10$^5$m. Il est donc concevable que la tache solaire puisse exister à des profondeurs sous la photosphère à l'intérieur d'une région convective du soleil sans que le fond de la tache solaire soit trop profond.
MODIFICATION AJOUTÉE : Dans les modèles de Solov'ev et Kirichek, par exemple, 2014, « la stabilité des taches solaires [est] une fonction de leur rayon et de la force de leur champ magnétique [qui] varie de manière monotone avec un rayon d'environ 700 G jusqu'à une limite asymptotique d'environ 4000 G. La profondeur de la dépression Wilson croît linéairement avec B. La gamme des équilibres stables est limitée de telle sorte que les taches solaires plus grandes (rayon supérieur à environ 12-18 mm) sont instables, ce qui peut expliquer l'absence de taches solaires très importantes sur le Soleil, ainsi que l'apparition des ponts lumineux dans les grandes taches solaires les divisant en plusieurs parties. Les taches solaires avec B dans la gamme de 2,6 à 2,7 kG et un rayon d'ombre d'environ 2 mm sont les plus stables. » Citation tirée de la note 4. de ce revue d'héliosismologie (également dans le dernier paragraphe ci-dessous), et voir la figure 22 de cette revue pour un schéma de leur modèle.
Dans la thèse que vous citez de B. Beeck, l'article principal trouvé ici , la géométrie de l'ombre (ni de la pénombre) n'est PAS connue a priori, ils font donc des suppositions et vérifient avec leurs simulations numériques détaillées. Ils varient systématiquement les conditions initiales, les conditions aux limites, l'intensité du champ magnétique et la profondeur de la tache solaire pour essayer de produire une tache solaire physiquement stable. Ils trouvent:
Les taches solaires stables nécessitent un champ magnétique > 4kG dans les couches souterraines. La structure (par exemple le gradient T) en dessous de z~2-3 mm semble être importante pour la stabilité des taches solaires. Cela indique également que les taches solaires ne peuvent pas être des phénomènes très superficiels. Ils concluent donc : les taches solaires stables ont besoin d'un champ magnétique de B 6 kG à des profondeurs de 5 à 6 mm.
Ils spéculent que cette exigence de stabilité peut exclure les géométries de taches solaires plates (c'est-à-dire pas profondes). Ils tentent de quantifier cela avec une géométrie en coin/dalle, où une intensité de champ magnétique plus élevée au bas de la tache solaire entraîne une intensité ombrale plus faible et une pénombre plus prononcée (voir la 5e diapositive à partir de la fin), qui pourraient être utilisées pour exclure par observation certains géométries des taches solaires.
EDIT AJOUT : Ainsi, les gammes d'échelles impliquées ici font partie d'un domaine de recherche actif. Il existe de nombreuses raisons théoriques de soupçonner que les taches solaires peuvent être profondes et larges, de l'ordre de ~Mm, mais nous ne pouvons sonder le soleil que si profondément, nous sommes donc généralement limités à ne voir que de l'ordre de ~$10^5$m, ce qui est cohérent avec la profondeur de la photosphère. Il en résulte que la structure et la profondeur exactes de l'ombre et de la pénombre ne sont pas bien comprises, actuellement, bien que la dépendance à l'égard de divers paramètres soit bien comprise dans certains cadres.
Juste après avoir posté cette réponse, j'ai réalisé que l'héliosismologie est un moyen d'essayer de contourner le problème de sonder plus profondément que la photosphère, et cela semble prometteur ! Les progrès de l'héliosismologie ont longtemps anticipé des informations sur l'intérieur du Soleil, par exemple ici et ici , qui ont donné des estimations comparables pour la profondeur des taches solaires, c'est-à-dire$\sim$1 mm. Je pense qu'il s'agit d'un domaine de recherche actif et qu'il sera intéressant de suivre son développement. Voir ici pour une critique (semi-)récente.