Quelle doit être la taille d'un code QR sur mon toit pour qu'un satellite puisse le scanner compte tenu de la résolution autorisée aujourd'hui?

Jan 26 2021

Dites, en utilisant les satellites Planet Labs

Merci

Réponses

7 uhoh Jan 28 2021 at 04:55

Quelle doit être la taille d'un code QR sur mon toit pour qu'un satellite puisse le scanner compte tenu de la résolution autorisée aujourd'hui?

Dites, en utilisant les satellites Planet Labs

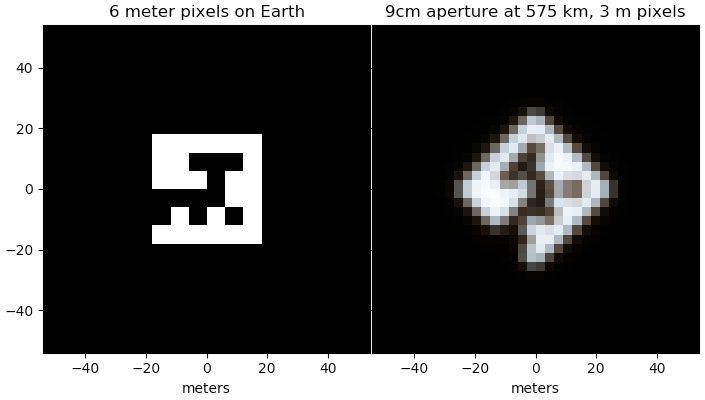
Ceci est une réponse supplémentaire. J'ai simulé des pixels «QR» de 6 mètres vus de l'espace avec une ouverture de 9 cm (à l'extrémité d'un cubesat Dove 3U) à des longueurs d'onde de 450, 550 et 650 nm, tourné à 45 degrés puis échantillonné avec des pixels de 3 mètres.

C'est un script décousu et fragile mais il fait le travail.

L'image soutient la conclusion principale de l' autre réponse selon laquelle c'est probablement la taille minimale pour une certaine fiabilité de la voir avec une colombe.

Le script est sous-optimal, j'étais paresseux et j'ai utilisé PIL pour faire une rotation, j'aurais pu interpoler avec scipy.ndimage.map_coordinates, et j'aurais pu "fuzzifier" avec scipy.ndimage.gaussian_filterau lieu d'un disque Airy sophistiqué.

Les teintes dans l'image finale sont dues aux limites de diffraction dépendant de la longueur d'onde de l'ouverture, le $1.22 \lambda / D$ variation de la résolution angulaire avec le rapport longueur d'onde sur ouverture.

import numpy as np
import matplotlib.pyplot as plt
import itertools
from PIL import Image
from scipy import special as spe
from scipy.ndimage import convolve

N = 5*2

data = ('111111' + '110001' + '111011' +
        '000011' + '010101' + '111111')
data = np.array([int(x) for x in data]).reshape((6, 6))
data = np.pad(data, ((6, 6), (6, 6)))

img = np.zeros((N*18, N*18, 3))

for i, j in itertools.product(np.arange(18), repeat=2):
    img[N*i:N*(i+1), N*j:N*(j+1)] = data[i, j]

pixsize = 6 # meters
scale = pixsize/N
extent = 9*N * scale * np.array([-1, 1, -1, 1])

R = 575 * 1000. # meters distance
x = 4*N * scale * np.linspace(-1, 1, 8*N)
X, Y = np.meshgrid(x, x)
q = np.sqrt(X**2 + Y**2)
wavelengths = 1E-09 * np.array([650, 550, 450])

a = 0.045 # radius of aperture in meters (looking out end of a 3U cubesat)
x = (2 * np.pi * a / wavelengths) * (q[..., None] / R)

# https://en.wikipedia.org/wiki/Airy_disk
airy = (2 * spe.j1(x) / x)**2
areas = airy.sum(axis=0).sum(axis=0)
airy /= areas

new = [convolve(img[..., i], airy[..., i]) for i in range(3)]
newarray = np.stack(new, axis=2)
newarray = np.uint8(255 * newarray/newarray.max())

newimg = Image.fromarray(newarray)
newimg45 = newimg.rotate(45)
newimg45.show()
n45 = np.array(list(newimg45.getdata())).reshape(18*2, N>>1, 18*2, N>>1, 3)
n45 = np.uint8(n45.sum(axis=(1, 3)) / (N>>1)**2)

if True:
    plt.figure()
    plt.subplot(1, 2, 1)
    plt.imshow(img, extent=extent)
    plt.title('6 meter pixels on Earth')
    plt.xlabel('meters')
    plt.subplot(1, 2, 2)
    plt.imshow(n45, extent=extent)
    plt.title('9cm aperture at 575 km, 3 m pixels')
    plt.xlabel('meters')
    plt.show()

4 uhoh Jan 27 2021 at 08:30

Quelle doit être la taille d'un code QR sur mon toit pour qu'un satellite puisse le scanner compte tenu de la résolution autorisée aujourd'hui?

Dites, en utilisant les satellites Planet Labs

tl; dr: en utilisant une " balise de réalité augmentée " 6x6 discutée dans la réponse de @ CamilleGoudeseune comme celle du rover Curiosity et 6 mètres de pixels (deux fois la résolution minimale pour permettre une translation et une rotation arbitraires), votre motif doit être de 36 x 36 mètres pour avoir un bon changement d'être repéré et récupéré à partir d'une image d'un PlanetLabs Dove.

Je supprimerais la réflectivité rouge et infrarouge des zones lumineuses et n'encoderais que dans les longueurs d'onde plus courtes, car les colombes ont quatre canaux de couleur sont (probablement) limités par la diffraction et les longueurs d'onde plus longues peuvent alors avoir une résolution plus mauvaise.

Essayez de n'exciter que les bandes de longueurs d'onde les plus courtes de votre vaisseau spatial ciblé pour les faire "pop-out" pour les téléspectateurs occasionnels, ou ne regardez ces longueurs d'onde dans le produit de données final si vous cherchez vous-même.

À https://www.planet.com/products/planet-imagery/les satellites les plus nombreux ou "Doves" fournissent des données pour le produit de données PLANETSCOPE. On dit que les satellites ont une résolution de 3,7 mètres et que le produit de données a une taille de pixel rééchantillonnée de 3 mètres. Voir aussi la réponse de @ djr à Ces images proviennent-elles de Planet Labs? Les images sont-elles accessibles au public?

Si vous étiez incroyablement chanceux d'avoir les pixels alignés avec votre motif QR à la fois en translation et en rotation, ils pourraient théoriquement mesurer 3 mètres.

Pratiquement cependant, étant donné la translation et la rotation arbitraires de votre motif dans le champ de l'image, vous devriez leur donner un facteur d' au moins 2 sinon 3 plus grand que cela.

@Uwe nous rappelle qu'un petit code QR serait encore assez gros. Il existe 11 x 11 codes Micro QR et les spacefolks ont utilisé des nombres de pixels encore plus petits pour des alternatives aux codes QR avec encore moins de pixels.