통계-박스 플롯
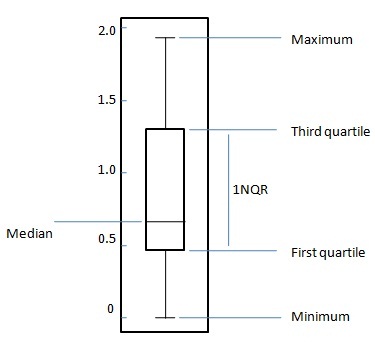
상자 그림은 다음 다섯 가지 숫자 요약을 기반으로 데이터 분포를 표시하는 표준화 된 방법입니다.
Minimum
1 분위
Median
3 분위
Maximum
균일하게 분포 된 데이터 세트의 경우 상자 그림 다이어그램에서 중앙 직사각형은 1 사분 위에서 3 사 분위 (또는 사 분위 간 범위, IQR)에 걸쳐 있습니다. 직사각형 내부의 선은 중앙값을 표시하고 상자 위와 아래의 "수염"은 최소값과 최대 값의 위치를 보여줍니다. 이러한 상자 그림은 최소에서 최대까지의 전체 변동 범위, 가능한 변동 범위, IQR 및 중앙값을 표시합니다.
문제 설명:
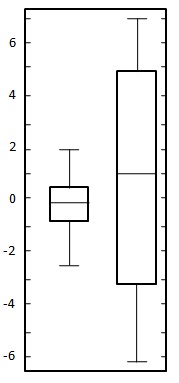
다음 두 데이터 세트에 대한 상자 그림을 만듭니다.
| 0.22 |
| -0.87 |
| -2.39 |
| -1.79 |
| 0.37 |
| -1.54 |
| 1.28 |
| -0.31 |
| -0.74 |
| 1.72 |
| 0.38 |
| -0.17 |
| -0.62 |
| -1.10 |
| 0.30 |
| 0.15 |
| 2.30 |
| 0.19 |
| -0.50 |
| -0.09 |
| -5.13 |
| -2.19 |
| -2.43 |
| -3.83 |
| 0.50 |
| -3.25 |
| 4.32 |
| 1.63 |
| 5.18 |
| -0.43 |
| 7.11 |
| 4.87 |
| -3.10 |
| -5.81 |
| 3.76 |
| 6.31 |
| 2.58 |
| 0.07 |
| 5.76 |
| 3.50 |
해결책:
여기서 두 데이터 세트는 모두 0 근처에서 균일하게 균형을 이루므로 평균은 0 근처입니다. 첫 번째 데이터 세트의 변동 범위는 약 -2.5 ~ 2.5이고 두 번째 데이터 세트의 범위는 약 -6 ~ 6입니다. 아래와 같이 차트를 그립니다.