통계-잔차 분석

잔차 분석은 잔차를 정의하고 잔차 그림 그래프를 조사하여 선형 회귀 모델의 적합성을 평가하는 데 사용됩니다.

잔여

잔차 ($ e $)는 관찰 된 값 ($ y $)과 예측 된 값 ($ \ hat y $)의 차이를 나타냅니다. 모든 데이터 포인트에는 하나의 잔차가 있습니다.

잔차 플롯

잔차 그림은 잔차가 세로 축에 있고 독립 변수가 가로 축에있는 그래프입니다. 점이 가로축 주위에 무작위로 분산되어있는 경우 선형 회귀 모델이 데이터에 적합합니다. 그렇지 않으면 비선형 모델을 선택하십시오.

잔차 그림의 유형

다음 예는 잔차 그림의 몇 가지 패턴을 보여줍니다.

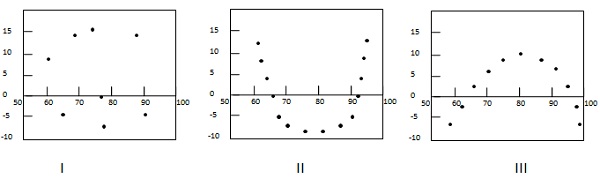
첫 번째 경우에는 점이 무작위로 분산됩니다. 따라서 선형 회귀 모델이 선호됩니다. 두 번째 및 세 번째 경우 점은 무작위로 분산되지 않으며 비선형 회귀 방법이 선호됨을 나타냅니다.

예

Problem Statement:

다음 데이터에 선형 회귀 모델이 적합한 지 확인하십시오.

$ x $	60	70	80	85	95
$ y $ (실제 가치)	70	65	70	95	85
$ \ hat y $ (예상 가치)	65.411	71.849	78.288	81.507	87.945

Solution:

Step 1: 각 데이터 포인트에 대한 잔차를 계산합니다.

$ x $	60	70	80	85	95
$ y $ (실제 가치)	70	65	70	95	85
$ \ hat y $ (예상 가치)	65.411	71.849	78.288	81.507	87.945
$ e $ (잔류)	4.589	-6.849	-8.288	13.493	-2.945

Step 2: -잔차 그래프를 그립니다.

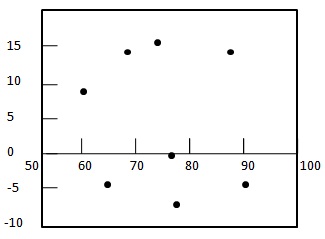
Step 3: -잔차의 임의성을 확인합니다.

여기서 잔차 플롯은 임의의 패턴을 나타냅니다. 첫 번째 잔차는 양수, 다음 두 개는 음수, 네 번째 잔차는 양수, 마지막 잔차는 음수입니다. 패턴은 매우 무작위 적이므로 선형 회귀 모델이 위의 데이터에 적합 함을 나타냅니다.