통계-데이터 패턴
데이터 패턴은 그래픽으로 그릴 때 매우 유용합니다. 중앙, 스프레드, 모양 및 기타 비정상적인 속성과 같은 기능 측면에서 일반적으로 설명되는 데이터 패턴입니다. 기타 특수 설명 레이블은 대칭, 종 모양, 기울어 진 등입니다.
센터
그래픽 적으로 분포의 중심은 분포의 중앙값에 있습니다. 이러한 그래픽 차트는 관측치의 거의 절반이 양쪽에 있음을 표시합니다. 각 열의 높이는 관측 빈도를 나타냅니다.
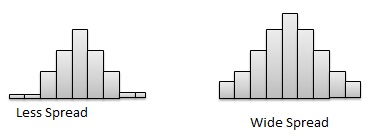
확산
분포의 산포는 데이터의 변동을 나타냅니다. 관측 세트가 넓은 범위를 포함하면 산포가 더 큽니다. 관측치가 단일 값을 중심으로하면 산포가 더 작아집니다.
모양
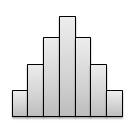
분포의 모양은 다음과 같은 특성을 사용하여 설명 할 수 있습니다.
Symmetry -대칭 분포에서 그래프는 각각의 절반이 서로 거울상이되도록 중앙에서 나눌 수 있습니다.

Number of peaks.-하나 또는 여러 개의 피크가있는 분포. 하나의 명확한 피크가있는 분포를 단봉이라고하고 두 개의 명확한 피크가있는 분포를 바이 모달이라고합니다. 중앙의 단일 피크 대칭 분포를 종 모양이라고합니다.
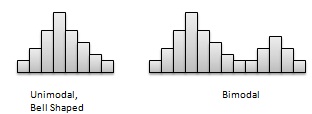
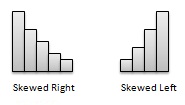
Skewness-일부 분포는 그래프의 한쪽에 다른 쪽보다 여러 개의 관측치를 가질 수 있습니다. 더 낮은 값에 대한 관측치가 적은 분포는 오른쪽으로 치우친다고합니다. 낮은 값에 대한 관측치가 적은 분포는 왼쪽으로 치우친다고합니다.
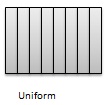
Uniform -관측치 세트에 피크가없고 데이터가 분포 범위에 균등하게 분산되어있는 경우 분포를 균일 분포라고합니다.
특이한 기능
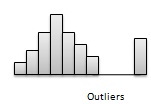
데이터 패턴의 일반적인 비정상적인 특징은 간격과 특이 치입니다.
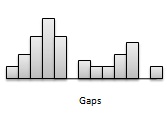
Gaps-간격은 관측치가없는 분포 영역을 가리 킵니다. 다음 그림은 분포 중간에 관측치가 없기 때문에 간격이 있습니다.
Outliers-분포는 다른 관측 데이터 세트와 크게 다른 극단 값을 특징으로 할 수 있습니다. 이러한 극단 값을 이상 값이라고합니다. 다음 그림은 특이 치가있는 분포를 보여줍니다.