통계-누적 포아송 분포
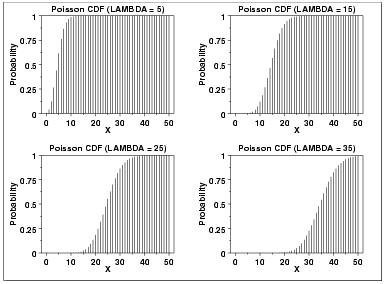
$ {\ lambda} $는 주어진 시간 간격에서 평균 이벤트 수를 나타내는 모양 매개 변수입니다. 다음은 $ {\ lambda} $의 4 개 값에 대한 포아송 확률 밀도 함수의 플롯입니다. 누적 분포 함수.
공식
$$ {F (x, \ lambda) = \ sum_ {k = 0} ^ x \ frac {e ^ {-\ lambda} \ lambda ^ x} {k!}} $$
어디-
$ {e} $ = 2.71828과 같은 자연 로그의 밑
$ {k} $ = 이벤트 발생 횟수; 그 확률은 함수에 의해 주어집니다.
$ {k!} $ = k의 계승
$ {\ lambda} $ = 주어진 간격 동안 예상되는 발생 횟수와 동일한 양의 실수
예
Problem Statement:
복잡한 소프트웨어 시스템은 5,000 줄의 코드 당 평균 7 개의 오류를 발생시킵니다. 무작위로 선택된 5,000 줄의 코드에서 정확히 2 개의 오류가 발생할 확률은 얼마입니까?
Solution:
임의로 선택된 5,000 줄의 코드에서 정확히 2 개의 오류가 발생할 확률은 다음과 같습니다.
$ {p (2,7) = \ frac {e ^ {-7} 7 ^ 2} {2!} = 0.022} $