통계-정규 분포

정규 분포는 대부분의 값이 범위의 중간에 클러스터되고 나머지 값이 양쪽 극단을 향해 대칭 적으로 가늘어지는 데이터 세트의 배열입니다. 키는 정규 분포 패턴을 따르는 간단한 예입니다. 대부분의 사람들은 평균 키를 가지고 있으며 평균보다 키가 크고 키가 작은 사람들의 수는 상당히 같으며 매우 적은 수 (여전히 거의 동일)는 극도로 적습니다. 다음은 정규 분포 곡선의 예입니다.

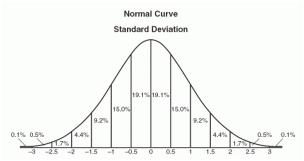
정규 분포의 그래픽 표현은 플레어 모양 때문에 종 곡선이라고도합니다. 정확한 모양은 인구 분포에 따라 다를 수 있지만 피크는 항상 중간에 있고 곡선은 항상 대칭입니다. 정규 분포에서 평균 모드와 중앙값은 모두 동일합니다.

공식

어디-

• $ {\ mu} $ = 평균

• $ {\ sigma} $ = 표준 편차

• $ {\ pi \ approx 3.14159} $

• $ {e \ approx 2.71828} $

예

Problem Statement:

일일 이동 시간을 조사한 결과 (분) :

26

33

65

28

34

55

25

44

50

36

26

37

43

62

35

38

45

32

28

34

평균은 38.8 분이고 표준 편차는 11.4 분입니다. 값을 z-점수로 변환하고 정규 분포 그래프를 준비합니다.

Solution:

우리가 사용해온 z- 점수 공식 :

어디-

• $ {z} $ = "z- 점수"(표준 점수)

• $ {x} $ = 표준화 할 값

• $ {\ mu} $ = 평균

• $ {\ sigma} $ = 표준 편차

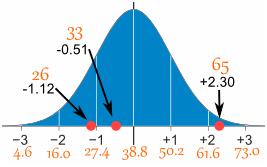
26을 변환하려면 :

먼저 평균을 뺍니다 : 26-38.8 = -12.8,

그런 다음 표준 편차로 나눕니다. -12.8 / 11.4 = -1.12

따라서 26은 평균에서 -1.12 표준 편차입니다.

다음은 처음 세 번의 전환입니다.

원래 가치	계산	표준 점수 (z- 점수)
26	(26-38.8) / 11.4 =	-1.12
33	(33-38.8) / 11.4 =	-0.51
65	(65-38.8) / 11.4 =	-2.30
...	...	...

그리고 여기에서는 다음을 그래픽으로 나타냅니다.