통계-중앙 극한 정리

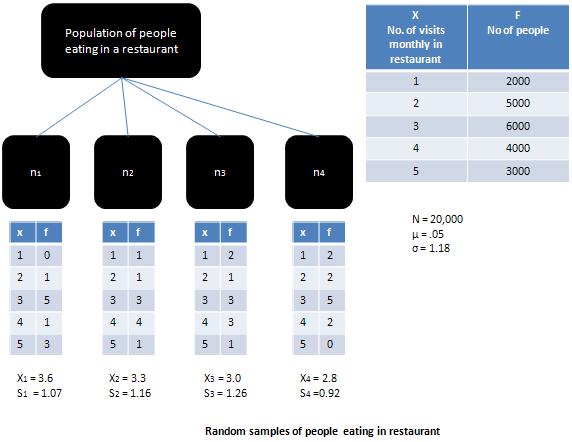
표본을 추출한 모집단이 정상 모집단이면 sample means 모집단 평균과 같고 sampling distribution정상입니다. 그림에 표시된 경우처럼 더 많은 인구가 치우치면sampling distribution 표본이 크면 (즉, 30보다 큼) 정규 분포에 더 가깝게 이동하는 경향이 있습니다.

에 따르면 Central Limit Theorem, 크기가 30보다 큰 충분히 큰 표본의 경우 sampling distribution 점점 더 normal distribution, 부모 모집단의 형태에 관계없이. 이 정리는population distribution 과 sampling distribution. 충분히 큰 샘플 세트가있는 경우sampling distribution 평균 접근 normal distribution. 중심 극한 정리의 중요성은 Richard에 의해 요약되었습니다. I. Levin은 다음과 같이 말합니다.

중심 극한 정리의 중요성은 표본에서 얻을 수있는 것 외에 해당 모집단의 빈도 분포 모양에 대해 알지 못해도 표본 통계를 사용하여 모집단 매개 변수에 대한 추론을 할 수 있다는 사실에 있습니다.