통계-감마 분포
감마 분포는 2- 모수 패밀리의 연속 확률 분포를 나타냅니다. 감마 분포는 일반적으로 세 가지 종류의 매개 변수 조합으로 고 안됩니다.
모양 매개 변수 $ k $ 및 축척 매개 변수 $ \ theta $.
모양 매개 변수 $ \ alpha = k $ 및 역 스케일 매개 변수 $ \ beta = \ frac {1} {\ theta} $, 비율 매개 변수라고합니다.
모양 매개 변수 $ k $ 및 평균 매개 변수 $ \ mu = \ frac {k} {\ beta} $.
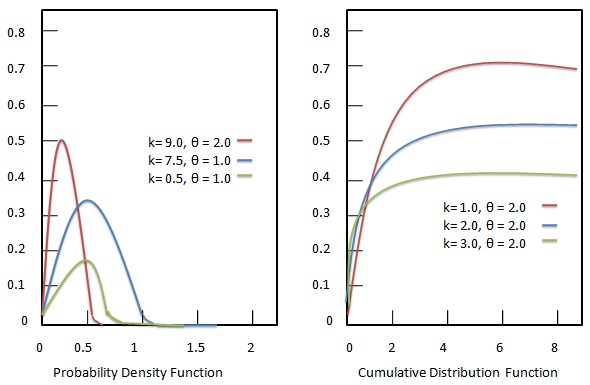
각 매개 변수는 양의 실수입니다. 감마 분포는 다음 기준에 따른 최대 엔트로피 확률 분포입니다.
공식
$ {E [X] = k \ theta = \ frac {\ alpha} {\ beta} \ gt 0 \ 및 \는 \ 고정입니다. \\ [7pt] E [ln (X)] = \ psi (k) + ln (\ theta) = \ psi (\ alpha)-ln (\ beta) \ 및 \는 \ 고정입니다. } $
어디-
$ {X} $ = 랜덤 변수.
$ {\ psi} $ = 디 감마 함수.
모양 $ \ alpha $ 및 요율 $ \ beta $를 사용한 특성화
확률 밀도 함수
감마 분포의 확률 밀도 함수는 다음과 같이 제공됩니다.
공식
어디-
$ {\ alpha} $ = 위치 매개 변수.
$ {\ beta} $ = 척도 매개 변수.
$ {x} $ = 랜덤 변수.
누적 분포 함수
감마 분포의 누적 분포 함수는 다음과 같이 제공됩니다.
공식
$ {F (x; \ alpha, \ beta) = \ int_0 ^ xf (u; \ alpha, \ beta) du = \ frac {\ gamma (\ alpha, \ beta x)} {\ Gamma (\ alpha)} } $
어디-
$ {\ alpha} $ = 위치 매개 변수.
$ {\ beta} $ = 척도 매개 변수.
$ {x} $ = 랜덤 변수.
$ {\ gamma (\ alpha, \ beta x)} $ = 더 낮은 불완전 감마 함수.
모양 $ k $ 및 척도 $ \ theta $를 사용한 특성화
확률 밀도 함수
감마 분포의 확률 밀도 함수는 다음과 같이 제공됩니다.
공식
어디-
$ {k} $ = 형상 매개 변수.
$ {\ theta} $ = 척도 매개 변수.
$ {x} $ = 랜덤 변수.
$ {\ Gamma (k)} $ = k에서 평가 된 감마 함수.
누적 분포 함수
감마 분포의 누적 분포 함수는 다음과 같이 제공됩니다.
공식
$ {F (x; k, \ theta) = \ int_0 ^ xf (u; k, \ theta) du = \ frac {\ gamma (k, \ frac {x} {\ theta})} {\ Gamma (k )}} $
어디-
$ {k} $ = 형상 매개 변수.
$ {\ theta} $ = 척도 매개 변수.
$ {x} $ = 랜덤 변수.
$ {\ gamma (k, \ frac {x} {\ theta})} $ = 더 낮은 불완전 감마 함수.