통계-첨도
분포의 꼬리 정도는 첨도로 측정됩니다. 분포가 정규 분포보다 어느 정도 이상 치가 발생하기 쉬운 (무거운 또는 가벼운 꼬리) 정도를 알려줍니다. Investopedia에서 제공하는 세 가지 유형의 곡선이 다음과 같이 표시됩니다.
모든 분포에서 꼬리가 0에 가깝기 때문에 밀도 플롯 (왼쪽 패널)에서 다양한 유형의 첨도를 식별하기가 어렵습니다. 그러나 꼬리의 차이는 일반 분위수-분위수 플롯 (오른쪽 패널)에서 쉽게 확인할 수 있습니다.
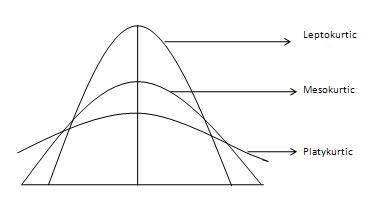
정규 곡선을 Mesokurtic 곡선이라고합니다. 분포의 곡선이 정규 곡선 또는 중간 곡선 곡선보다 더 이상 치가 발생하기 쉬운 (또는 꼬리가 더 두꺼운) 경우이를 Leptokurtic 곡선이라고합니다. 곡선이 정상 곡선보다 특이 치 경향이 적거나 꼬리가 가벼운 경우이를 platykurtic 곡선이라고합니다. 첨도는 모멘트로 측정되며 다음 공식으로 제공됩니다.
공식
$ {\ beta_2 = \ frac {\ mu_4} {\ mu_2}} $
어디-
$ {\ mu_4 = \ frac {\ sum (x- \ bar x) ^ 4} {N}} $
\ beta_2의 값이 클수록 곡선이 더 뾰족하거나 뾰족합니다. 정규 곡선의 값은 3이고, leptokurtic은 \ beta_2가 3보다 크고 platykurtic은 \ beta_2가 3보다 작습니다.
예
Problem Statement:
공장에서 일하는 45 명의 노동자의 일급 데이터가 제공됩니다. 평균에 대한 모멘트를 사용하여 \ beta_1 및 \ beta_2를 계산합니다. 결과에 대해 설명합니다.
| 임금 (Rs.) | 근로자 수 |
|---|---|
| 100-200 | 1 |
| 120-200 | 2 |
| 140-200 | 6 |
| 160-200 | 20 |
| 180-200 | 11 |
| 200-200 | 삼 |
| 220-200 | 2 |
Solution:
| 임금 (Rs.) |
근로자 수 (f) |
중간 점 m |
m-$ {\ frac {170} {20}} $ 일 |
$ {fd} $ | $ {fd ^ 2} $ | $ {fd ^ 3} $ | $ {fd ^ 4} $ |
|---|---|---|---|---|---|---|---|
| 100-200 | 1 | 110 | -삼 | -삼 | 9 | -27 | 81 |
| 120-200 | 2 | 130 | -2 | -4 | 8 | -16 | 32 |
| 140-200 | 6 | 150 | -1 | -6 | 6 | -6 | 6 |
| 160-200 | 20 | 170 | 0 | 0 | 0 | 0 | 0 |
| 180-200 | 11 | 190 | 1 | 11 | 11 | 11 | 11 |
| 200-200 | 삼 | 210 | 2 | 6 | 12 | 24 | 48 |
| 220-200 | 2 | 230 | 삼 | 6 | 18 | 54 | 162 |
| $ {N = 45} $ | $ {\ sum fd = 10} $ | $ {\ sum fd ^ 2 = 64} $ | $ {\ sum fd ^ 3 = 40} $ | $ {\ sum fd ^ 4 = 330} $ |
편차는 가정 된 평균에서 가져 왔으므로 먼저 임의의 원점에 대한 모멘트를 계산 한 다음 평균에 대한 모멘트를 계산합니다. 임의의 기원 '170'에 대한 순간
평균에 대한 순간
평균에 대한 이동 값에서 이제 $ {\ beta_1} $ 및 $ {\ beta_2} $를 계산할 수 있습니다.
위의 계산을 통해 왜도를 측정하는 $ {\ beta_1} $는 거의 0이어서 분포가 거의 대칭 적이라는 것을 알 수 있습니다. $ {\ beta_2} $ 첨도를 측정하는 값이 3보다 크므로 분포가 렙토 쿠르트임을 의미합니다.