통계-역 감마 분포
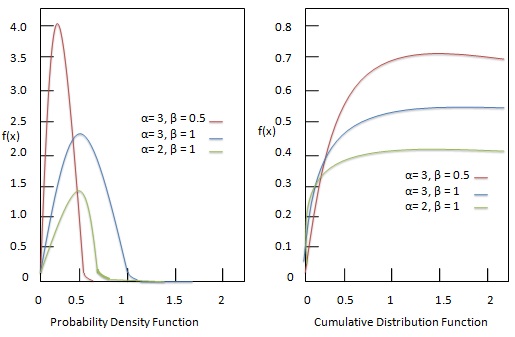
역 감마 분포는 양의 형태 매개 변수 $ {\ alpha, \ beta} $ 및 위치 매개 변수 $ {\ mu} $를 갖는 감마 확률 밀도 함수의 역수입니다. $ {\ alpha} $는 높이를 제어합니다. $ {\ alpha} $가 높을수록 확률 밀도 함수 (PDF)가 더 커집니다. $ {\ beta} $는 속도를 제어합니다. 다음 식으로 정의됩니다.
공식
$ {f (x) = \ frac {x ^ {-(\ alpha + 1)} e ^ {\ frac {-1} {\ beta x}}} {\ Gamma (\ alpha) \ beta ^ \ alpha} \\ [7pt] \, 여기서 x \ gt 0} $
어디-
$ {\ alpha} $ = 양의 모양 매개 변수.
$ {\ beta} $ = 긍정적 인 모양 매개 변수.
$ {x} $ = 랜덤 변수.
다음 다이어그램은 다양한 매개 변수 조합이있는 확률 밀도 함수를 보여줍니다.