फर्मियन भौतिकी द्वारा

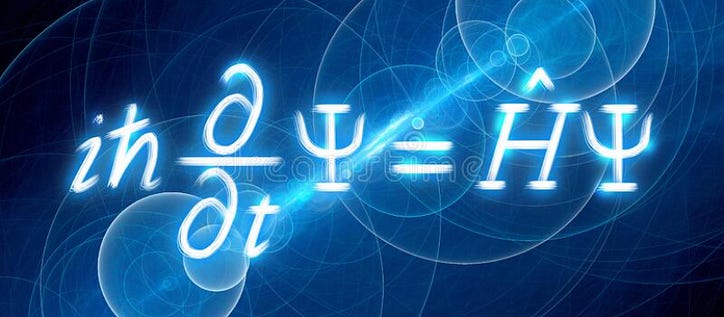
यदि आपने क्वांटम भौतिकी ली है, या कम से कम इसके बारे में सुना है, तो आपने इस श्रोडिंगर आदमी के बारे में सुना होगा। तुम्हें पता है - पूरी बिल्ली वाली चीज़ वाला? ठीक है, वह क्वांटम यांत्रिकी - श्रोडिंगर समीकरण में सबसे उपयोगी समीकरणों में से एक के पीछे भी आदमी है। पहली नज़र में, समीकरण को हल करना असंभव लग सकता है (और वास्तव में कुछ मामलों में, यह है!), लेकिन इसे पढ़ने के बाद, आप समीकरण को समझेंगे और यहां तक ​​कि एक परिदृश्य के लिए इसे कैसे हल करें। तैयार? चलिए चलते हैं।

यहाँ समीकरण है। यह डरावना लगता है — इसमें कांटे भी होते हैं! लेकिन आइए इस समीकरण पर कुछ अंतर्ज्ञान हासिल करने का प्रयास करें। हम सबसे पहले क्वांटम यांत्रिकी में ऊर्जा के बारे में बात करके, उन्हें ऑपरेटरों को बढ़ावा देकर, फिर तरंग फ़ंक्शन की भूमिका के बारे में बात करके शुरू करेंगे। उसके बाद, हम सब कुछ एक साथ सिलाई करेंगे और समीकरण को हल करेंगे।

शास्त्रीय यांत्रिकी

शास्त्रीय यांत्रिकी (और क्वांटम यांत्रिकी) में, ऊर्जा का सूत्र E = KE + PE है जहां E कुल ऊर्जा है, KE गतिज ऊर्जा है, और PE स्थितिज ऊर्जा है। अब केई और पीई को लिखने में थोड़ा समय लगता है, इसलिए लिखने के कुछ मिलीसेकंड को बचाने के लिए, भौतिकविद गतिज और संभावित ऊर्जा का प्रतिनिधित्व करने के लिए क्रमशः टी और वी के स्पष्ट प्रतीकों का उपयोग करते हैं। तो अब हमारे पास वह E = T + V है

फुटनोट: यदि आपने शास्त्रीय यांत्रिकी ली है तो आप देख सकते हैं कि हम हैमिल्टनियन फॉर्मूलेशन का उपयोग कर रहे हैं! हम Lagrangian सूत्रीकरण के साथ एक और दिन निपटेंगे।

अब हम जानते हैं कि T=p²/2m (गतिज ऊर्जा का सूत्र)। यहाँ, m=द्रव्यमान, p=संवेग, और सभी का सबसे कठिन प्रतीक, ½=आधा। मास हमेशा स्थिर रहता है, लेकिन गति का होना जरूरी नहीं है। यदि कोई किसी वस्तु पर बल लगाता है, तो संवेग बदलना शुरू हो जाएगा और अपने मूल मान से विचलित हो जाएगा। अब संभावित ऊर्जा के बारे में क्या?

स्थितिज ऊर्जा का सूत्र है V= -(F का समाकल) जहां F बल है। यह स्पष्ट हो जाता है कि संभावित ऊर्जा किसी वस्तु पर लगाए गए बल पर निर्भर करती है। अलग-अलग परिदृश्यों में, आपकी संभावित ऊर्जा अलग-अलग मान ले सकती है क्योंकि अलग-अलग बल हैं। उदाहरण के लिए, एक गुरुत्वाकर्षण कुएं में, क्षमता V=mgx है, लेकिन एक हार्मोनिक दोलक में, क्षमता V=(1/2)kx² हो जाती है। यह बहुत महत्वपूर्ण है क्योंकि यह पता चला है कि हमारे "परिदृश्य" जहां हम अपने श्रोडिंगर समीकरण को हल करते हैं, वास्तव में केवल अलग-अलग संभावनाएं हैं। यह बाद में समझ में आएगा।

पहला परिमाणीकरण

अब क्वांटम यांत्रिकी में, हम अपने "अवलोकन" (टी और ई) लेते हैं और उन्हें ऑपरेटर बनाते हैंसमकक्षों। हमारे उद्देश्यों के लिए एक ऑपरेटर केवल एक ऐसा कार्य है जो एक मान लेता है और दूसरे को थूक देता है। तो टी में गतिज ऊर्जा ऑपरेटर समकक्ष होता है, जिसे आमतौर पर टी 'के साथ दर्शाया जाता है, और ऊर्जा ऊर्जा ऑपरेटर समकक्ष पर ले जाती है, जिसे आमतौर पर एच के साथ चिह्नित किया जाता है। संभावित ऊर्जा को हल करने के बजाय "दिया" जाता है, इसलिए इसमें कोई नहीं है ऑपरेटर समकक्ष। अब काइनेटिक एनर्जी ऑपरेटर को एक ऑपरेटर के रूप में परिभाषित किया जाता है, जहां जब यह वेव फंक्शन पर काम करता है, तो यह वेवफंक्शन द्वारा कण की गतिज ऊर्जा को गुणा करता है। एनर्जी ऑपरेटर के साथ भी यही बात है। यह पूरी बात थोड़ी बेकार और सारगर्भित लग सकती है, लेकिन मुझ पर विश्वास करें कि यह नहीं है - हम वहां पहुंच रहे हैं। अब याद करें कि कैसे T=(1/2m)p²? इसका तात्पर्य है कि T' = (1/2m)p̂², जहाँ p̂ संवेग संकारक है। और पहले की तरह, p̂ ψ = p ψजहां पी कण की गति है (फिर से, एक ऑपरेटर फ़ंक्शन पर कार्य करता है और फ़ंक्शन को ऑपरेटर से संबंधित किसी भी मान से गुणा करता है)। अब यह पता चला है कि संवेग संचालक है

पी = -ह (डी / डीएक्स)। इसे अभी के लिए दिए गए के रूप में लें। यह बताता है कि

T' = -h²/2m (d²/dx²)। और चूँकि E = T + V, तब H=(-h²/2m)(d²/dx²) + V. तब हम दोनों पक्षों को वेव फंक्शन से गुणा करके प्राप्त कर सकते हैं

एच ψ = -h²/2m (d²ψ/dx²) + Vψ

और पहले से याद रखें, H ψ = Eψ, इसलिए

ई ψ = (-h²/2m)(d²ψ/dx²) + Vψ

अब गहरी सांस लें। हमने बहुत गणित किया है और उम्मीद है कि आप हारे नहीं हैं। यह पता चला है कि हमने श्रोडिंगर समीकरण को "व्युत्पन्न" किया है! अब इससे पहले कि हम इसे हल करने के बारे में बात करें, हमें इस बारे में बात करने की आवश्यकता है कि यह "वेवफंक्शन" क्या है।

वेवफंक्शन क्या है?

शास्त्रीय यांत्रिकी में, हम एक कण के लिए गति के समीकरणों को हल करने के लिए शास्त्रीय हैमिल्टनियन समीकरण का उपयोग करते हैं। गति के समीकरण सिर्फ उस समय के समीकरण हैं जहां एक कण एक निश्चित समय पर होता है। उदाहरण के लिए, मुक्त कण के लिए गति का समीकरण x(t)=vt + x0 है। यदि हमारे पास प्रारंभिक स्थिति और वेग है तो हम किसी भी क्षण के लिए कण की स्थिति का पता लगा सकते हैं। क्वांटम यांत्रिकी में, हम "वेवफंक्शन" नामक किसी चीज़ को खोजने के लिए श्रोडिंगर समीकरण का उपयोग करते हैं। वेवफंक्शन स्वयं शारीरिक रूप से सार्थक नहीं है - इसका कोई मतलब नहीं है और यह आपको (सीधे) कुछ भी नहीं बताता है। जो सार्थक है वह वेवफंक्शन का वर्ग है जो आपको संभाव्यता घनत्व देता है. संभाव्यता घनत्व केवल एक फ़ंक्शन है जो आपको मौका बताता है कि जब आप इसे मापते हैं तो आप किसी सीमा में एक कण पाते हैं। तो हम तब कह सकते हैं कि तरंग फलन संभाव्यता घनत्व का "वर्गमूल" मात्र है। अब हमारे पास श्रोडिंगर समीकरण क्या है, इस बारे में बात करने के लिए अंत में सभी पृष्ठभूमि ज्ञान हैं ।

जैसा कि हम उपरोक्त समीकरण से देख सकते हैं, संभावित ऊर्जा वी (एक्स) को छोड़कर सब कुछ स्थिर है। हम एक विशेष संभावित ऊर्जा लेते हैं, और उस मामले के लिए समीकरण को हल करते हैं जहां आपके पास वह विशेष संभावित ऊर्जा होती है। यह बहुत सुंदर है, क्योंकि इससे कोई फर्क नहीं पड़ता कि आपके सिस्टम पर क्या तनाव है, या गर्मी, आवेश, वोल्टेज, आप इसे नाम दें - आपको इनमें से किसी का भी हिसाब करने की आवश्यकता नहीं है। आपको केवल संभावित ऊर्जा फलन जानने की आवश्यकता है और आप समीकरण को हल कर सकते हैं

(यदि हम यहां पांडित्यपूर्ण होना चाहते हैं, तो हम कह सकते हैं कि "तकनीकी रूप से", हम उन सभी चीजों को क्षमता के अंदर ही शामिल कर रहे हैं। साथ ही, दूसरी व्युत्पत्ति के लिए उलटा त्रिकोण चीज छोटा है)

हिसाब

(यदि आपको कैलकुलस पसंद नहीं है तो आप इस भाग को छोड़ सकते हैं)

अब, एक सरल विभव के लिए श्रोडिंगर समीकरण को हल करते हैं जहाँ हर जगह V(x)=0 है। इसे एक मुक्त कण के रूप में जाना जाता है, क्योंकि इस पर नेट बल शून्य हैं। यह सभी दमन से मुक्त है! शास्त्रीय मामले में, गति का समीकरण होगा x(t)=vt + x0 जो स्पेस-टाइम ग्राफ पर एक सीधी रेखा बनाता है। आइए देखें कि क्वांटम केस के लिए वेव फंक्शन कैसा दिखता है।

चूँकि V(x) = 0, तब श्रोडिंगर समीकरण बन जाता है

-एच²/2एम (डी² ψ/डीएक्स²) = ईψ

फिर हम कुछ पुनर्व्यवस्थित कर सकते हैं और प्राप्त कर सकते हैं

d² ψ/dx² = -2mEψ/h²

अब हम देख सकते हैं कि ψ को छोड़कर दाईं ओर के सभी पद स्थिर हैं । यह अच्छा है क्योंकि इससे समीकरण को हल करना आसान हो जाता है। फिर हम एक स्थिर k को sqrt(2mE/h) के रूप में परिभाषित कर सकते हैं, जिसका अर्थ है कि अब हमारे पास है

d²ψ / dx² = -k²ψ

हम फिर समीकरण के दोनों पक्षों को दाहिने हाथ की अवधि से जोड़ते हैं

d²ψ/dx² + k²ψ = 0

फिर हम मानते हैं कि ψ(x) = exp(rx)

और इससे हमें मिलता है

r=-k², r= +ik या -ik

इसका मतलब है कि ψ( x)=exp(ikx) या

ψ( x)=exp(-ikx)

चूंकि समीकरण रैखिक है, हम सामान्य समाधान प्राप्त करने के लिए दोनों भागों का सुपरपोजिशन (रैखिक संयोजन) ले सकते हैं

ψ(x) = Aexp(ikx) + Beexp(-ikx)

और हम तकनीकी रूप से कर रहे हैं। आप सोच रहे होंगे कि हम स्थिरांक A और B कैसे निर्धारित कर सकते हैं। हम आमतौर पर इसे सामान्यीकरण नामक किसी चीज़ के द्वारा करते हैं, लेकिन यह कहानी फिर कभी। यह पता चला है कि इस परिदृश्य के लिए सामान्यीकृत नहीं किया जा सकता है। वेव फ़ंक्शन के लिए फैंसी भाषा शून्य तक नहीं पहुंचती है क्योंकि आप अनंत या माइनस अनंत तक जाते हैं। तो किसके लिए A और B मान इस अवस्था के अनुरूप हैं? वैसे यह पता चला है कि यह वास्तव में एक संभावित स्थिति नहीं है क्योंकि आप इसे सामान्य नहीं कर सकते। उफ़!

हालांकि चिंता मत करो! यह पता चला है कि सभी संभावित तरंगों की एक सुपरपोजिशन वास्तविक स्थिति उत्पन्न कर सकती है। यह अपने आप में बहुत सी अच्छी चीजें लाता है - लेकिन वह भी अगली बार के लिए एक कहानी है।

पढ़ने के लिए धन्यवाद! यह वेबसाइट गणितीय प्रतीकों को प्रारूपित करने में एक भयानक काम करती है, इसलिए कुछ गणित पाठ अच्छी तरह से प्रदर्शित नहीं हुए। यदि आप एक ही चीज़ का वीडियो व्युत्पत्ति देखना चाहते हैं, तो मैंने समाधान पर अपने चैनल Fermion Physics पर एक वीडियो बनाया है (हालाँकि मैं काफी तेज़ बात करता हूँ)। वीडियो और इस लेख के बीच स्विच करने से समाधान को और स्पष्ट करने में मदद मिलेगी। अगली बार तक!