สามารถใช้ต้นไม้ Stern-Brocot เพื่อการบรรจบกันของ $2^m/3^n$เหรอ?
การอ่านข้อกำหนดเบื้องต้น:
- สามารถประมาณค่าจริงเชิงบวกเป็น $2^m/3^n$ ด้วย $(m,n)$ ใหญ่พอ?
- ลำดับต้นไม้ Stern Brocot
เหตุผลที่ฉันมองหาขั้นตอนที่ไม่มีข้อเสียเปรียบนี้กล่าวคือการประมาณครั้งต่อไปมักจะใกล้เคียงกับผลลัพธ์ที่ต้องการมากขึ้น นี่คือสิ่งที่ฉันได้พยายามจนถึงตอนนี้
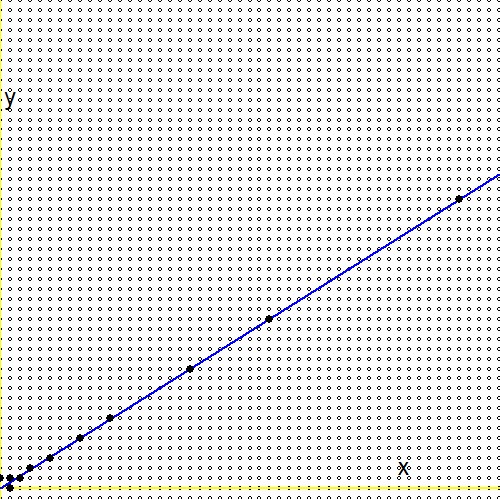
ตามคำถาม (2. ) สำหรับจำนวนจริงที่เป็นบวกทุกตัว$0 \lt g \lt 1$มีลำดับที่ไม่สิ้นสุดในต้นไม้ Stern Brocot [.. ] ที่มาบรรจบกันเป็นจำนวนจริง ในขณะเดียวกันคำถามนี้มี คำตอบและผลลัพธ์หลักในนั้นอ่านดังนี้: $$ - \frac{1}{n_1(n_1+n_2)} \lt g - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} $$ ในมุมมองของคำถาม (1. ) เราแทนที่ $\ln(2)/\ln(3)$ สำหรับตัวเลขนั้น $g$. จากนั้นเป็นไปตามนั้น: $$ - \frac{1}{n_1(n_1+n_2)} \lt \frac{\ln(2)}{\ln(3)} - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} \\ - \frac{\ln(3)}{n_1} \lt \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \lt + \frac{\ln(3)}{n_2} \\ \ln\left(3^{-1/n_1}\right) \lt \ln\left(\frac{2^{n_1+n_2}}{3^{m_1+m_2}}\right) \lt \ln\left(3^{+1/n_2}\right) \\ 3^{-1/n_1} \lt \frac{2^{n_1+n_2}}{3^{m_1+m_2}} \lt 3^{+1/n_2} $$การค้นหาผ่านต้นไม้ Stern-Brocot สามารถมองเห็นได้ เส้นสีน้ำเงินคือฟังก์ชัน $\,\color{blue}{x\ln(2)-y\ln(3)=0}\,$วงกลมเล็ก ๆ คือเศษส่วนที่แมปบนเส้นตาราง $\,m/n \to (m,n)\,$จุดที่เต็มไปด้วยสีดำจำนวนมากคือเศษส่วนในต้นไม้ Stern-Brocot จะเห็นว่าการค้นหาผ่านต้นไม้นั้นมีประสิทธิภาพมากกว่าการเพิ่มจำนวนมาก $m$ และ $n$ โดยเพิ่มทีละครั้ง
ตอนนี้เปรียบเทียบนิพจน์ที่บรรทัดที่สองของสูตรข้างต้นกับนิพจน์ที่คล้ายคลึงกันในการอ้างอิง (1): $$ \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \quad \Longleftrightarrow \quad m\ln(2) - n\ln(3) - \ln(r) $$ และเตรียมพร้อมสำหรับความผิดหวัง: ลอการิทึมของจริงตามอำเภอใจ $r$ที่ขาดหายไป! หรืออีกทางหนึ่ง:$\ln(r)=0$ หรือ $r=1$. ซึ่งหมายความว่า "การค้นหาที่ไม่มีที่สิ้นสุด" ของเราผ่านทางต้นไม้ Stern-Brocot แม้ว่าจะมีประสิทธิภาพสูง แต่ในที่สุดก็มาถึงค่าประมาณสำหรับอันดับหนึ่งเท่านั้น ฉันคิดว่าสิ่งนี้แปลกเพราะ - ในเชิงภาพ - ดูเหมือนจะไม่มีความแตกต่างอย่างมากระหว่าง$\color{red}{2^m/3^n \to r}$ และ $\color{blue}{2^m/3^n \to 1}$:
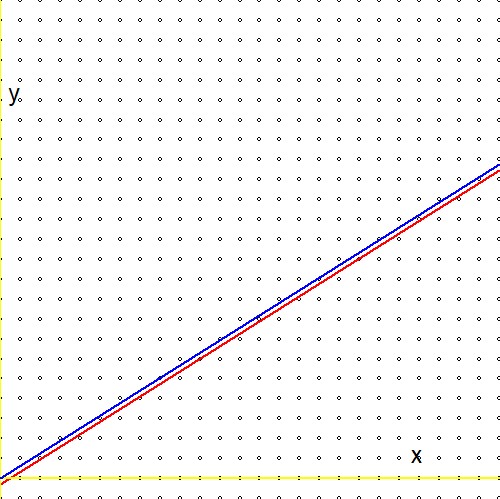
ดังนั้นคำถาม: มีวิธีการปรับขั้นตอน Stern-Brocot เพื่อให้ใช้กับ reals อื่นที่ไม่ใช่หรือไม่?
แก้ไข
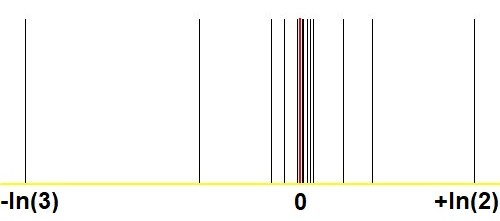
นี่คือกราฟอีกอันที่แสดงการบรรจบกันที่น่าอัศจรรย์ด้วยวิธี Stern-Brocot โดยเปรียบเทียบกับรูปภาพที่คล้ายคลึงกันใน Q & A ของฉัน สามารถประมาณค่าจริงเชิงบวกใด ๆ ได้โดยประมาณเป็น$2^m/3^n$ ด้วย $(m,n)$ใหญ่พอ? :
คำตอบ
ฉันจะให้แนวทางที่ไม่ใช้ขั้นตอน Stern-Brocot
มันพอเพียงที่จะแสดงให้เห็นว่า $\frac{2^{m}}{3^{n}}$มีความหนาแน่นในช่วงเวลา [1,2] ตั้งแต่การ$\alpha\in (0,\infty)$ นอกช่วงเวลานี้มีบางอย่าง $k\in Z$ ดังนั้น $\alpha = 2^{k}\gamma $ สำหรับบางคน $\gamma \in [1,2]$. จากนั้นเรารู้ว่ามีลำดับใน$\frac{2^{m}}{3^{n}}$ แนวทางไหน $\gamma$คูณลำดับตามลำดับด้วย $2^{k}$ (อาจใช้หางของลำดับ) เราได้ลำดับใน $\frac{2^{m}}{3^{n}}$ แนวทางไหน $\alpha$.
ถัดไปพิจารณาว่าแผนที่ $f:[1,2] -> [0,1]$ ด้วย $f(x) = log_{2}(x)$ เป็นอคติ
ภาพของ $\frac{2^{m}}{3^{n}}$ ใต้แผนที่คือ $N-Nlog_{2}(3)$. ดังนั้นจึงเพียงพอที่จะแสดงให้เห็นว่า$N-Nlog_{2}(3)$ มีความหนาแน่นใน $[0,1]$.
นี่เป็นผลมาจากทฤษฎีบท Equidistribution ของ Weyl ซึ่งเป็นกรณีพิเศษของทฤษฎีบทเออร์โกดิก
พิจารณา $a=2-log_{2}(3) = log_{2}(\frac{4}{3})$ดังนั้น $a$ อยู่ในภาพของชุดดังนั้นคือ $na = log_{2}(\frac{4^{n}}{3^{n}})$ และก็คือส่วนที่เป็นเศษส่วนของ $na$.
ทฤษฎีบทการกระจายความเท่าเทียมกันของ weyl (ซึ่งไม่ใช่ผลลัพธ์เล็กน้อย) แสดงให้เห็นว่าส่วนที่เป็นเศษส่วนของ $na$มีการกระจายอย่างสม่ำเสมอและด้วยเหตุนี้จึงหนาแน่นบน [0,1] ตั้งแต่$2-log_{2}(3)$ ไม่มีเหตุผลคุณสามารถใช้ทฤษฎีบทนี้