L'arbre de Stern-Brocot peut-il être utilisé pour une meilleure convergence des $2^m/3^n$?
Lecture préalable :
- Tout réel positif peut-il être approximé comme$2^m/3^n$avec$(m,n)$assez large?
- Séquence d'arbres Stern Brocot
Raison pour laquelle je cherchais une procédure qui ne présente pas cet inconvénient, c'est-à-dire où la prochaine approximation est toujours plus proche du résultat souhaité. C'est ce que j'ai essayé jusqu'à présent.
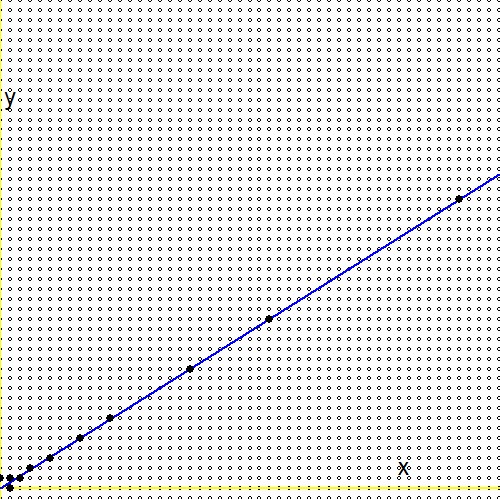
D'après la question (2.), pour tout nombre réel positif$0 \lt g \lt 1$, il existe une suite infinie dans l'arbre de Stern Brocot [ .. ] qui converge vers le nombre réel. Pendant ce temps, cette question a une réponse , et le résultat principal se lit comme suit : $$ - \frac{1}{n_1(n_1+n_2)} \lt g - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} $$Compte tenu de la question (1.), on substitue $\ln(2)/\ln(3)$pour ce numéro $g$. Il s'ensuit alors que : $$ - \frac{1}{n_1(n_1+n_2)} \lt \frac{\ln(2)}{\ln(3)} - \frac{m_1+m_2}{n_1+n_2} \lt \frac{1}{(n_1+n_2)n_2} \\ - \frac{\ln(3)}{n_1} \lt \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \lt + \frac{\ln(3)}{n_2} \\ \ln\left(3^{-1/n_1}\right) \lt \ln\left(\frac{2^{n_1+n_2}}{3^{m_1+m_2}}\right) \lt \ln\left(3^{+1/n_2}\right) \\ 3^{-1/n_1} \lt \frac{2^{n_1+n_2}}{3^{m_1+m_2}} \lt 3^{+1/n_2} $$La recherche à travers l'arbre Stern-Brocot peut être illustrée. La ligne bleue est la fonction $\,\color{blue}{x\ln(2)-y\ln(3)=0}\,$, les petits cercles sont des fractions, cartographiés sur une grille $\,m/n \to (m,n)\,$, les points remplis massivement de noir sont les fractions de l'arbre de Stern-Brocot. On voit que la recherche dans l'arbre est beaucoup plus efficace que l'augmentation $m$et $n$avec des incréments un à la fois.
Comparez maintenant l'expression à la deuxième ligne des formules ci-dessus avec une expression analogue dans la référence (1.):$$ \ln(2)(n_1+n_2) - \ln(3)(m_1+m_2) \quad \Longleftrightarrow \quad m\ln(2) - n\ln(3) - \ln(r) $$Et préparez-vous à une déception : le logarithme du réel arbitraire$r$est manquant! Ou bien:$\ln(r)=0$ou$r=1$. Cela signifie que notre "recherche infinie" à travers l'arbre de Stern-Brocot, bien que très efficace, arrive finalement à une approximation uniquement pour le numéro un. Je trouve cela bizarre, car - graphiquement - il ne semble pas y avoir de grande différence entre$\color{red}{2^m/3^n \to r}$et$\color{blue}{2^m/3^n \to 1}$:
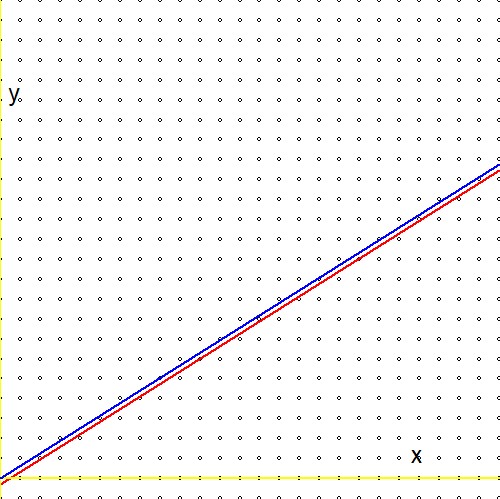
D'où la QUESTION : existe-t-il un moyen d'adapter la procédure de Stern-Brocot de manière à ce qu'elle fonctionne pour des réels autres que un ?
ÉDITER.
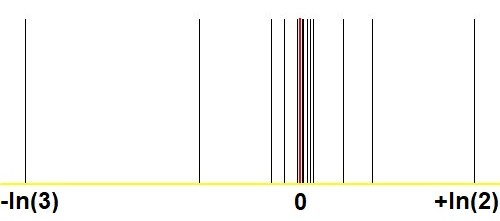
Voici un autre graphique qui montre l'étonnante convergence avec la méthode Stern-Brocot, en comparaison avec des images analogues dans mon Q & A. Tout réel positif peut-il être approximé comme$2^m/3^n$avec$(m,n)$assez large? :
Réponses
Je vais donner une approche qui n'utilise pas la procédure de Stern-Brocot.
Il suffit de montrer que$\frac{2^{m}}{3^{n}}$est dense dans l'intervalle [1,2]. Depuis la prise$\alpha\in (0,\infty)$en dehors de cet intervalle il y a quelques$k\in Z$pour que$\alpha = 2^{k}\gamma $pour certains$\gamma \in [1,2]$. Nous savons alors qu'il existe une suite dans$\frac{2^{m}}{3^{n}}$qui s'approche$\gamma$, en multipliant terme à terme la suite par$2^{k}$(en prenant éventuellement une queue de la séquence), on obtient une séquence en$\frac{2^{m}}{3^{n}}$qui s'approche$\alpha$.
Considérez ensuite que la carte$f:[1,2] -> [0,1]$avec$f(x) = log_{2}(x)$est une bijection.
L'image de$\frac{2^{m}}{3^{n}}$sous la carte est$N-Nlog_{2}(3)$. Il suffit donc de montrer que$N-Nlog_{2}(3)$est dense en$[0,1]$.
Ceci est une conséquence du théorème d'équidistribution de Weyl, qui est un cas particulier du théorème ergodique.
Considérer$a=2-log_{2}(3) = log_{2}(\frac{4}{3})$, alors$a$est à l'image de l'ensemble, ainsi est$na = log_{2}(\frac{4^{n}}{3^{n}})$ainsi que la partie fractionnaire de$na$.
Le théorème d'équidistribution de weyl (qui n'est pas un résultat trivial) montre que pour a irrationnel la partie fractionnaire de$na$est uniformément distribuée et donc dense sur [0,1]. Depuis$2-log_{2}(3)$est irrationnel, vous pouvez utiliser ce théorème.