Por Fermion Física

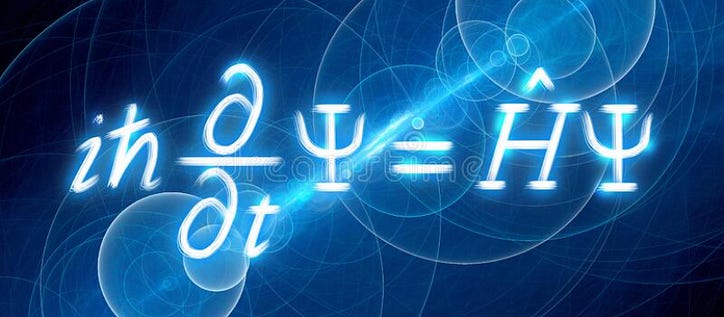
Si has estudiado física cuántica, o al menos has oído hablar de ella, es posible que hayas oído hablar de este tipo Schrödinger. Ya sabes, ¿el que tiene todo el asunto del gato? Bueno, también es el tipo detrás de una de las ecuaciones más útiles de la mecánica cuántica: la ecuación de Schrödinger. A primera vista, la ecuación puede parecer imposible de resolver (¡y de hecho, en algunos casos lo es!), pero después de leer esto, comprenderá la ecuación e incluso cómo resolverla para un escenario. ¿Listo? Vamos.

Aquí está la ecuación. Da miedo, ¡incluso tiene horquillas! Pero tratemos de ganar algo de intuición en esta ecuación. Primero comenzaremos hablando sobre la energía en la mecánica cuántica, promocionándolos a los operadores y luego hablando sobre el papel de la función de onda. Después de eso, uniremos todo y resolveremos la ecuación.

Mecanica clasica

En mecánica clásica (y mecánica cuántica), la fórmula para la energía es E = KE + PE, donde E es energía total, KE es energía cinética y PE es energía potencial. Ahora, KE y PE tardan un poco en escribirse, por lo que para ahorrar unos pocos milisegundos de escritura, los físicos usan los símbolos obvios de T y V para representar la energía cinética y potencial respectivamente. Entonces ahora tenemos que E = T + V

Nota al pie: ¡Si ha tomado mecánica clásica, puede notar que estamos usando la formulación hamiltoniana! Nos ocuparemos de la formulación lagrangiana otro día.

Ahora sabemos que T=p²/2m (fórmula de la energía cinética). Aquí, m=masa, p=cantidad de movimiento y el símbolo más complicado de todos, ½=mitad. La masa siempre es constante, pero el impulso no tiene por qué serlo. Si alguien aplica una fuerza a un objeto, el impulso comenzará a cambiar y se desviará de su valor original. Ahora, ¿qué pasa con la energía potencial?

La fórmula para la energía potencial es V= -(integral de F) donde F es la fuerza. Se hace evidente que la energía potencial depende de la fuerza aplicada a un objeto. En diferentes escenarios, tu energía potencial puede tomar diferentes valores ya que hay diferentes fuerzas. Por ejemplo, en un pozo gravitacional, el potencial es V=mgx, pero en un oscilador armónico, el potencial se convierte en V=(1/2)kx². Esto es muy importante porque resulta que nuestros "escenarios" en los que resolvemos nuestra ecuación de Schrödinger son en realidad solo potenciales diferentes. Esto tendrá sentido más adelante.

Primera cuantización

Ahora, en mecánica cuántica, tomamos nuestros "observables" (T y E) y les hacemos tener un operadorcontrapartes Un operador para nuestros propósitos es solo una función que toma un valor y escupe otro. Entonces, T tiene una contraparte de operador de energía cinética, generalmente denotada con T', y la energía toma una contraparte de operador de energía, generalmente denotada con H. La energía potencial está "dada" en lugar de resolverse, por lo que no tiene ninguna contraparte del operador. Ahora el operador de energía cinética se define como un operador donde cuando actúa sobre la función de onda, devuelve la energía cinética de la partícula multiplicada por la función de onda. Lo mismo con el operador de Energía. Todo esto puede parecer un poco inútil y abstracto, pero confía en mí, no lo es: estamos llegando allí. Ahora recuerda cómo T=(1/2m)p²? Esto implica que T' = (1/2m)p̂², donde p̂ es el operador de cantidad de movimiento. Y como antes, p̂ ψ = p ψdonde p es el momento de la partícula (nuevamente, un operador actúa sobre una función y devuelve la función multiplicada por cualquier valor relacionado con el operador). Ahora resulta que el operador de cantidad de movimiento es

p̂ = -ih(d/dx). Tómalo como un hecho por ahora. Esto implica que

T' = -h²/2m (d²/dx²). Y como E = T + V, entonces H=(-h²/2m)(d²/dx²) + V. Ahora podemos multiplicar ambos lados por la función de onda para obtener

Hψ = -h²/2m (d²ψ/dx²) + Vψ

Y recuerda de antes, H ψ = Eψ, entonces

mi ψ = (-h²/2m)(d²ψ/dx²) + Vψ

Ahora toma una respiración profunda. Hicimos muchas matemáticas y esperamos que no estés perdido. ¡Resulta que acabamos de “derivar” la ecuación de Schrödinger! Ahora, antes de hablar sobre cómo resolverlo, debemos hablar sobre qué es esta "función de onda".

¿Qué es una función de onda?

En mecánica clásica, usamos la ecuación hamiltoniana clásica para resolver las ecuaciones de movimiento de una partícula. Las ecuaciones de movimiento son solo las ecuaciones para saber dónde se encuentra una partícula en un momento dado. Por ejemplo, la ecuación de movimiento de una partícula libre es x(t)=vt + x0. Podemos encontrar la posición de la partícula para cualquier momento si tenemos la posición inicial y la velocidad. En mecánica cuántica, en cambio, usamos la ecuación de Schrödinger para encontrar algo llamado "función de onda". La función de onda en sí no tiene significado físico, no significa nada y no te dice nada (directamente). Lo que es significativo es el cuadrado de la función de onda que te da la densidad de probabilidad. La densidad de probabilidad es solo una función que te dice la probabilidad de que encuentres una partícula en algún rango cuando la mides. Entonces podemos decir que la función de onda es solo la "raíz cuadrada" de la densidad de probabilidad. Ahora finalmente tenemos todo el conocimiento previo para hablar sobre lo que es la ecuación de Schrödinger .

Como podemos ver en la ecuación anterior, todo es constante excepto la energía potencial V(x). Tomamos una energía potencial particular y resolvemos la ecuación para el caso en el que tienes esa energía potencial particular. Esto es tan hermoso, porque no importa qué estrés haya en su sistema, o el calor, la carga, el voltaje, lo que sea, no necesita tener en cuenta nada de eso. Todo lo que necesita saber es solo la función de energía potencial y puede resolver la ecuación

(Si queremos ser pedantes aquí, podríamos decir que "técnicamente", estamos incorporando todas esas cosas dentro del potencial mismo. Además, el triángulo invertido es la abreviatura de la segunda derivada)

Cálculo

(si no te gusta el cálculo, puedes saltarte esta parte)

Ahora, resolvamos la ecuación de Schrödinger para un potencial simple donde V(x)=0 en todas partes. Esto se conoce como partícula libre, ya que las fuerzas netas sobre ella son cero. ¡Es libre de toda opresión! En el caso clásico, la ecuación de movimiento sería x(t)=vt + x0, que forma una línea recta en un gráfico de espacio-tiempo. Veamos cómo se ve la función de onda para el caso cuántico.

Dado que V(x)=0, la ecuación de Schrödinger se convierte en

-h²/2m(d² ψ/dx²) = Eψ

Entonces podemos hacer algunos reordenamientos y obtener

d² ψ/dx² = -2mEψ/h²

Ahora podemos ver que todos los términos del lado derecho son constantes excepto ψ. Esto es bueno porque hace que la ecuación sea fácil de resolver. Entonces podemos definir una constante k para que sea sqrt(2mE/h), lo que significa que ahora tenemos

d²ψ / dx² = -k²ψ

Luego sumamos ambos lados de la ecuación por el término de la derecha

d²ψ/dx² + k²ψ = 0

Entonces asumimos que ψ(x) = exp(rx)

y de esto obtenemos

r=-k², r= +ik o -ik

Esto significa que ψ( x)=exp(ikx) o

ψ( x)=exp(-ikx)

Como la ecuación es lineal, podemos tomar una superposición (combinación lineal) de ambas partes para obtener la solución general

ψ(x) = Aexp(ikx) + Bexp(-ikx)

y técnicamente hemos terminado. Quizás se pregunte cómo podemos determinar las constantes A y B. Por lo general, haríamos esto mediante algo llamado normalización, pero esa es una historia para otro momento. Resulta que para este escenario no se puede normalizar. Ese es un lenguaje elegante para la función de onda que no se acerca a cero a medida que avanza hacia el infinito o menos el infinito. Entonces, ¿para qué valores A y B corresponden a este estado? Bueno, resulta que este no es realmente un estado posible ya que no puedes normalizarlo. ¡Ups!

¡Pero no te preocupes! Resulta que una superposición de todas las funciones de onda posibles puede producir un estado real. Esto trae muchas cosas geniales propias, pero esa también es una historia para la próxima vez.

¡Gracias por leer! Este sitio web hace un trabajo terrible al dar formato a los símbolos matemáticos, por lo que parte del texto matemático no se mostró bien. Si desea ver una derivación en video de lo mismo, hice un video aquí en mi canal Fermion Physics sobre la solución (aunque hablo bastante rápido). Cambiar entre el video y este artículo ayudará a que la solución sea más clara. ¡Hasta la próxima!