Statistik - Distribusi Beta

Distribusi beta mewakili distribusi probabilitas kontinu yang diparameterisasi oleh dua parameter bentuk positif, $ \ alpha $ dan $ \ beta $, yang muncul sebagai eksponen variabel acak x dan mengontrol bentuk distribusi.

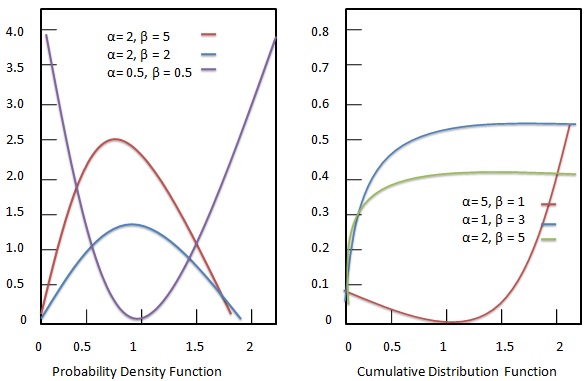
Fungsi kepadatan probabilitas

Fungsi kepadatan probabilitas dari distribusi Beta diberikan sebagai:

Rumus

$ {f (x) = \ frac {(xa) ^ {\ alpha-1} (bx) ^ {\ beta-1}} {B (\ alpha, \ beta) (ba) ^ {\ alpha + \ beta- 1}} \ hspasi {.3in} a \ le x \ le b; \ alpha, \ beta> 0 \\ [7pt] \, di mana \ B (\ alpha, \ beta) = \ int_ {0} ^ {1} {t ^ {\ alpha-1} (1-t) ^ { \ beta-1} dt}} $

Dimana -

$ {\ alpha, \ beta} $ = parameter bentuk.
$ {a, b} $ = batas atas dan bawah.
$ {B (\ alpha, \ beta)} $ = Fungsi beta.

Distribusi Beta Standar

Dalam kasus memiliki batas atas dan bawah sebagai 1 dan 0, distribusi beta disebut distribusi beta standar. Ini didorong oleh rumus berikut:

Rumus

$ {f (x) = \ frac {x ^ {\ alpha-1} (1-x) ^ {\ beta-1}} {B (\ alpha, \ beta)} \ hspace {.3in} \ le x \ le 1; \ alpha, \ beta> 0} $

Fungsi distribusi kumulatif

Fungsi distribusi kumulatif dari distribusi Beta diberikan sebagai:

Rumus

$ {F (x) = I_ {x} (\ alpha, \ beta) = \ frac {\ int_ {0} ^ {x} {t ^ {\ alpha-1} (1-t) ^ {\ beta- 1} dt}} {B (\ alpha, \ beta)} \ hspace {.2in} 0 \ le x \ le 1; p, \ beta> 0} $

Dimana -

$ {\ alpha, \ beta} $ = parameter bentuk.
$ {a, b} $ = batas atas dan bawah.
$ {B (\ alpha, \ beta)} $ = Fungsi beta.

Ini juga disebut rasio fungsi beta tidak lengkap.