Statistik - Kurtosis
Derajat kemiringan distribusi diukur dengan kurtosis. Ini memberi tahu kita sejauh mana distribusi lebih atau kurang rawan pencilan (lebih berat atau ringan) daripada distribusi normal. Tiga jenis kurva yang berbeda, milik Investopedia, ditunjukkan sebagai berikut -
Sulit untuk membedakan jenis kurtosis dari plot kepadatan (panel kiri) karena ekor mendekati nol untuk semua distribusi. Namun perbedaan ekor mudah dilihat pada plot kuantil-kuantitatif normal (panel kanan).
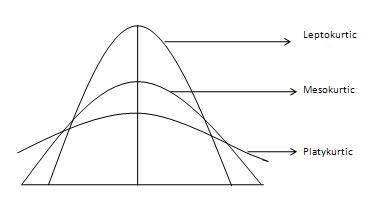
Kurva normal disebut kurva Mesokurtik. Jika kurva distribusi lebih rawan pencilan (atau lebih berat-tailed) daripada kurva normal atau mesokurtik maka itu disebut sebagai kurva Leptokurtik. Jika kurva kurang rentan terhadap pencilan (atau lebih terang) daripada kurva normal, ini disebut kurva platykurtic. Kurtosis diukur dengan momen dan diberikan dengan rumus berikut -
Rumus
$ {\ beta_2 = \ frac {\ mu_4} {\ mu_2}} $
Dimana -
$ {\ mu_4 = \ frac {\ sum (x- \ bar x) ^ 4} {N}} $
Semakin besar nilai \ beta_2 kurva semakin memuncak atau leptokurtik. Kurva normal memiliki nilai 3, leptokurtik memiliki \ beta_2 lebih besar dari 3 dan platykurtic memiliki \ beta_2 kurang dari 3.
Contoh
Problem Statement:
Data upah harian 45 pekerja pabrik diberikan. Hitung \ beta_1 dan \ beta_2 menggunakan momen tentang mean. Komentari hasilnya.
| Upah (Rs.) | Jumlah Pekerja |
|---|---|
| 100-200 | 1 |
| 120-200 | 2 |
| 140-200 | 6 |
| 160-200 | 20 |
| 180-200 | 11 |
| 200-200 | 3 |
| 220-200 | 2 |
Solution:
| Upah (Rs.) |
Jumlah Pekerja (f) |
Nilai tengah m |
b - $ {\ frac {170} {20}} $ d |
$ {fd} $ | $ {fd ^ 2} $ | $ {fd ^ 3} $ | $ {fd ^ 4} $ |
|---|---|---|---|---|---|---|---|
| 100-200 | 1 | 110 | -3 | -3 | 9 | -27 | 81 |
| 120-200 | 2 | 130 | -2 | -4 | 8 | -16 | 32 |
| 140-200 | 6 | 150 | -1 | -6 | 6 | -6 | 6 |
| 160-200 | 20 | 170 | 0 | 0 | 0 | 0 | 0 |
| 180-200 | 11 | 190 | 1 | 11 | 11 | 11 | 11 |
| 200-200 | 3 | 210 | 2 | 6 | 12 | 24 | 48 |
| 220-200 | 2 | 230 | 3 | 6 | 18 | 54 | 162 |
| $ {N = 45} $ | $ {\ sum fd = 10} $ | $ {\ sum fd ^ 2 = 64} $ | $ {\ sum fd ^ 3 = 40} $ | $ {\ sum fd ^ 4 = 330} $ |
Karena penyimpangan telah diambil dari mean yang diasumsikan, maka pertama-tama kita menghitung momen tentang asal sewenang-wenang dan kemudian momen tentang mean. Momen tentang asal yang sewenang-wenang '170'
Momen tentang kejam
Dari nilai pergerakan tentang mean, sekarang kita dapat menghitung $ {\ beta_1} $ dan $ {\ beta_2} $:
Dari perhitungan diatas dapat disimpulkan bahwa $ {\ beta_1} $ yang mengukur kemiringan hampir nol, sehingga menunjukkan bahwa distribusinya hampir simetris. $ {\ beta_2} $ Yang mengukur kurtosis, memiliki nilai lebih dari 3, sehingga menyiratkan bahwa distribusinya bersifat leptokurtik.