Statistik - Analisis sisa

Analisis residual digunakan untuk menilai kesesuaian model regresi linier dengan mendefinisikan residual dan memeriksa grafik plot residual.

Sisa

Sisa ($ e $) mengacu pada perbedaan antara nilai observasi ($ y $) vs nilai prediksi ($ \ hat y $). Setiap titik data memiliki satu residu.

Petak Sisa

Plot residual adalah grafik di mana residual berada pada sumbu vertikal dan variabel bebas berada pada sumbu horizontal. Jika titik-titik tersebar secara acak di sekitar sumbu horizontal, maka model regresi linier sesuai untuk data; jika tidak, pilih model non-linier.

Jenis Petak Sisa

Contoh berikut menunjukkan beberapa pola di petak sisa.

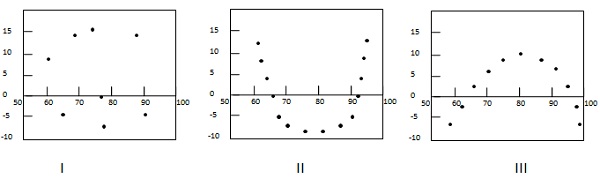
Dalam kasus pertama, titik-titik tersebar secara acak. Jadi model regresi linier lebih disukai. Dalam kasus kedua dan ketiga, titik-titik tidak tersebar secara acak dan menunjukkan bahwa metode regresi non-linier lebih disukai.

Contoh

Problem Statement:

Periksa di mana model regresi linier sesuai untuk data berikut.

$ x $	60	70	80	85	95
$ y $ (Nilai Aktual)	70	65	70	95	85
$ \ hat y $ (Nilai Prediksi)	65.411	71.849	78.288	81.507	87.945

Solution:

Step 1: Hitung residu untuk setiap titik data.

$ x $	60	70	80	85	95
$ y $ (Nilai Aktual)	70	65	70	95	85
$ \ hat y $ (Nilai Prediksi)	65.411	71.849	78.288	81.507	87.945
$ e $ (Sisa)	4.589	-6,849	-8.288	13.493	-2,945

Step 2: - Gambar grafik plot sisa.

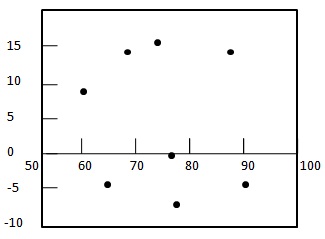
Step 3: - Periksa keacakan residu.

Di sini plot residual menunjukkan pola acak - Residual pertama positif, dua negatif, keempat positif, dan residual terakhir negatif. Karena pola cukup acak yang menunjukkan bahwa model regresi linier sesuai untuk data di atas.