Statistik - Distribusi Poisson Kumulatif

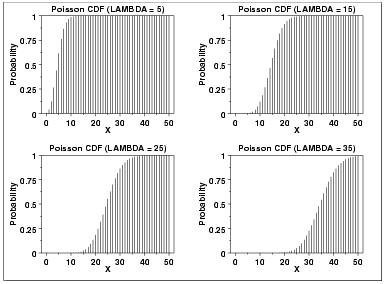
$ {\ lambda} $ adalah parameter bentuk yang menunjukkan jumlah rata-rata kejadian dalam interval waktu tertentu. Berikut ini adalah plot fungsi kepadatan probabilitas Poisson untuk empat nilai $ {\ lambda} $. Fungsi Distribusi Kumulatif.

Rumus

$$ {F (x, \ lambda) = \ sum_ {k = 0} ^ x \ frac {e ^ {- \ lambda} \ lambda ^ x} {k!}} $$

Dimana -

$ {e} $ = Basis dari logaritma natural sama dengan 2,71828
$ {k} $ = Jumlah kemunculan suatu peristiwa; probabilitas yang diberikan oleh fungsi.
$ {k!} $ = Faktorial dari k
$ {\ lambda} $ = Bilangan riil positif, sama dengan jumlah kejadian yang diharapkan selama interval tertentu

Contoh

Problem Statement:

Sistem perangkat lunak yang kompleks menghasilkan rata-rata 7 kesalahan per 5.000 baris kode. Berapa probabilitas dari tepat 2 kesalahan dalam 5.000 baris dari baris kode yang dipilih secara acak?

Solution:

Probabilitas tepat 2 kesalahan dalam 5.000 baris dari baris kode yang dipilih secara acak adalah:

$ {p (2,7) = \ frac {e ^ {- 7} 7 ^ 2} {2!} = 0,022} $