Statistik - Distribusi Gamma
Distribusi gamma mewakili distribusi probabilitas kontinu dari keluarga dua parameter. Distribusi gamma umumnya dirancang dengan tiga jenis kombinasi parameter.
Parameter bentuk $ k $ dan parameter skala $ \ theta $.
Parameter bentuk $ \ alpha = k $ dan parameter skala terbalik $ \ beta = \ frac {1} {\ theta} $, disebut sebagai parameter tarif.
Parameter bentuk $ k $ dan parameter rata-rata $ \ mu = \ frac {k} {\ beta} $.
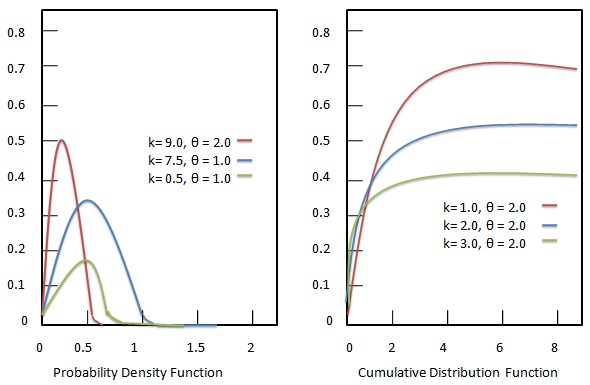
Setiap parameter adalah bilangan real positif. Distribusi gamma adalah distribusi probabilitas entropi maksimum yang didorong oleh kriteria berikut.
Rumus
$ {E [X] = k \ theta = \ frac {\ alpha} {\ beta} \ gt 0 \ dan \ is \ diperbaiki. \\ [7pt] E [ln (X)] = \ psi (k) + ln (\ theta) = \ psi (\ alpha) - ln (\ beta) \ dan \ is \ tetap. } $
Dimana -
$ {X} $ = Variabel acak.
$ {\ psi} $ = fungsi digamma.
Karakterisasi menggunakan bentuk $ \ alpha $ dan beri nilai $ \ beta $
Fungsi kepadatan probabilitas
Fungsi kepadatan probabilitas dari distribusi Gamma diberikan sebagai:
Rumus
Dimana -
$ {\ alpha} $ = parameter lokasi.
$ {\ beta} $ = parameter skala.
$ {x} $ = variabel acak.
Fungsi distribusi kumulatif
Fungsi distribusi kumulatif dari distribusi Gamma diberikan sebagai:
Rumus
$ {F (x; \ alpha, \ beta) = \ int_0 ^ xf (u; \ alpha, \ beta) du = \ frac {\ gamma (\ alpha, \ beta x)} {\ Gamma (\ alpha)} } $
Dimana -
$ {\ alpha} $ = parameter lokasi.
$ {\ beta} $ = parameter skala.
$ {x} $ = variabel acak.
$ {\ gamma (\ alpha, \ beta x)} $ = menurunkan fungsi gamma tidak lengkap.
Karakterisasi menggunakan bentuk $ k $ dan skala $ \ theta $
Fungsi kepadatan probabilitas
Fungsi kepadatan probabilitas dari distribusi Gamma diberikan sebagai:
Rumus
Dimana -
$ {k} $ = parameter bentuk.
$ {\ theta} $ = parameter skala.
$ {x} $ = variabel acak.
$ {\ Gamma (k)} $ = fungsi gamma dievaluasi pada k.
Fungsi distribusi kumulatif
Fungsi distribusi kumulatif dari distribusi Gamma diberikan sebagai:
Rumus
$ {F (x; k, \ theta) = \ int_0 ^ xf (u; k, \ theta) du = \ frac {\ gamma (k, \ frac {x} {\ theta})} {\ Gamma (k )}} $
Dimana -
$ {k} $ = parameter bentuk.
$ {\ theta} $ = parameter skala.
$ {x} $ = variabel acak.
$ {\ gamma (k, \ frac {x} {\ theta})} $ = menurunkan fungsi gamma tidak lengkap.