
Есть печально известная цитата , приписываемая тренеру НБА и бывшему игроку Джейсону Кидду: «Мы собираемся развернуть эту команду на 360 градусов!»
Упс. Учителя математики, должно быть, закатили глаза.
Как вы, возможно, уже знаете, круг состоит ровно из 360 градусов. Если бы Кидд сдержал свое обещание, то его команда развернулась бы в полном порядке. Проблема в том, что отряд не перестанет вращаться, пока не «совершит полный круг» и не окажется там же, где начал.
Не рецепт улучшения. Кидд хотел развернуть свою команду на 180 градусов и сделать их победителями!
Степени, определенные
В данном контексте градус — это единица измерения углов . На бумаге степени представлены символом степени, который выглядит так: °
Таким образом, вместо того, чтобы писать « 18 градусов», вы можете просто написать « 18 ° » .
Одним из важнейших понятий в тригонометрии и геометрии является прямой угол . Это угол, который образуется при пересечении двух перпендикулярных линий .
Он также представляет четверть полного оборота.
Допустим, вы хотите что-то физически повернуть. Что-нибудь. Вы выбрали фиксированную центральную точку и пытаетесь маневрировать этим объектом вокруг нее круговым движением. Если вы закончите работу и сделаете полный круг, это будет полный оборот. Но если вы остановите процесс на 25 процентах пути, это только одна четверть полного оборота. Что дает вам прямой угол.
Прямой угол равен 90 градусам (т. е. 25 процентам от 360). Вот еще один способ выразить это : прямой угол равен π/2 радианам .
Тайм-аут! Что такое радиан? И как в этом замешано число π ( пи )?
Распаковка радианов
Хорошо, представьте идеальный круг. Есть прямая линия, которая начинается в его точном центре и заканчивается на изогнутом периметре круга (например, на внешнем краю).
По определению, эта линия является радиусом нашей окружности.
По сути, радиан — это часть круга. Посмотрите на изогнутый внешний периметр круга еще раз. Теперь представьте себе отрезок периметра, длина которого равна радиусу вашего круга. Если вы нарисуете две прямые линии, соединяющие две его конечные точки с точным центром круга, то угол, который они образуют, будет равен радиану.
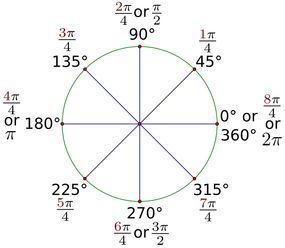
В каждом круге есть место для одинакового количества радиан. Это число равно удвоенному числу пи ("π"). Поскольку число пи равно примерно 3,14, можно сказать, что в окружности приблизительно 6,28 радиана (2 х 3,14). Или что 1 радиан равен примерно 57,29 градусам (180°/π).
Радиан против. Степени
Послушайте, мы не будем этого отрицать. Радианы могут быть более сложной концепцией для визуализации, чем градусы.
Но не сбрасывайте со счетов первое. Оба этих угловых измерительных устройства имеют свои преимущества.
Диплом более популярен. В реальном мире вы, скорее всего, встретите людей, которые думают в градусах, а не в радианах. Итак, если вы пытаетесь общаться с нематематиком, возможно, придерживайтесь степеней.
Однако в исчислении радианы хороши, потому что они поддаются гораздо более простым уравнениям . Будущие студенты AP захотят иметь это в виду.
Преобразование градусов в радианы (и наоборот)
Чтобы преобразовать градусы в радианы, вам просто нужно запомнить несколько простых шагов.
Во-первых, возьмите количество градусов, которое вы хотите конвертировать. Умножьте это число на π радиан/180 градусов . Удалив некоторые избыточные единицы, а затем немного упростив, вы получите ответ.
Предположим, у вас есть металлический стержень, согнутый под углом 120 градусов. Как это выразить в радианах?
Чтобы узнать это, мы напишем наше уравнение так:
120 ° х (π радиан/180 ° )
Обратите внимание на пару символов степени, показанных выше. Они компенсируют друг друга, гарантируя, что наш окончательный ответ будет в радианах. Теперь у нас осталось:
120 х (π радиан/180)
Сделайте умножение, и вы получите 120π/180 радиан . Но мы еще не совсем закончили. Теперь нам нужно упростить нашу дробь, если это возможно. Нам нужно определить наибольшее целое число, которое можно точно разделить как на знаменатель (180), так и на не-π часть числителя (120). Спойлер: в нашем случае магическое число — 60.
Если вы на самом деле разделите 120π и 180 на 60, вы получите 2π/3 радиана.
Итак, поехали: 120° равно 2π/3 радианам.
Переход от радианов к градусам — аналогичная процедура . Только в этом случае мы возьмем начальное количество радиан и умножим его на (180 ° / π ).
π/3 радиан х (180 ° / π) = 60 градусов
Обобщить:
Чтобы перевести из радианов в градусы : умножьте на 180, разделите на π
Чтобы преобразовать градусы в радианы : умножьте на π, разделите на 180.
Теперь это интересно
Форма «кольца», состоящая из двух концентрических окружностей с общим центром, технически называется « кольцом ».















































