
Hay una cita infame atribuida al entrenador de la NBA y exjugador Jason Kidd: "¡Vamos a darle un giro de 360 grados a este equipo!".
¡Vaya! Los profesores de matemáticas deben haber puesto los ojos en blanco ante eso.
Como ya sabrás, un círculo se compone exactamente de 360 grados. Si Kidd hubiera cumplido su promesa, entonces su equipo habría dado la vuelta. El problema es que el escuadrón no dejaba de girar hasta que "había completado el círculo" y terminaba justo donde empezó.
No es una receta para mejorar. ¡Lo que Kidd buscaba era dar un giro de 180 grados a su equipo y hacerlos ganadores!
Grados, Definidos
El grado , en este contexto, es una unidad que podemos usar para medir ángulos . En el papel, los grados están representados por el símbolo de grado, que se ve así: °
Entonces, en lugar de escribir " 18 grados" , podrías simplemente escribir " 18 ° " .
Uno de los conceptos más importantes en trigonometría y geometría es el ángulo recto . Este es el ángulo que se forma donde se cruzan dos líneas perpendiculares .
También representa un cuarto de una rotación completa.
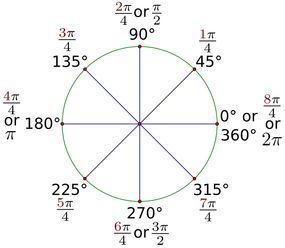
Digamos que quieres convertir algo físicamente. Cualquier cosa. Ha elegido un punto central fijo y está tratando de maniobrar ese objeto alrededor de él con un movimiento circular. Si termina el trabajo y hace un círculo completo, eso es una rotación completa. Pero si detiene el proceso el 25 por ciento del camino, eso es solo una cuarta parte de una rotación completa. Lo que te da un ángulo recto.
Un ángulo recto es igual a 90 grados (es decir, el 25 por ciento de 360). Aquí hay otra forma de expresarlo : un ángulo recto es igual a π/2 radianes .
¡Se acabó el tiempo! ¿Qué es un radián? ¿Y cómo se mezcló π ( pi ) en esto?
Desempaquetando Radianes
Bien, imagina un círculo perfecto. Hay una línea recta que comienza en su centro exacto y termina en el perímetro curvo del círculo (como en el borde exterior).
Por definición, esa línea es el radio de nuestro círculo.
Esencialmente, un radián es una porción de un círculo. Mira el perímetro exterior curvo del círculo una vez más. Ahora imagina un segmento del perímetro que tiene la misma longitud que el radio de tu círculo. Si dibujaras dos líneas rectas que conectan sus dos extremos con el centro exacto del círculo, el ángulo que producirían sería un radián.
Cada círculo tiene espacio para el mismo número de radianes. Ese número es igual a 2 veces pi ("π"). Dado que pi es igual a aproximadamente 3,14, se podría decir que hay aproximadamente 6,28 radianes en un círculo (2 x 3,14). O que 1 radián son aproximadamente 57,29 grados (180°/π).
Radianes vs. Grados
Mira, no lo negaremos. Los radianes pueden ser un concepto más difícil de visualizar que los grados.
Pero no descartes lo primero. Ambas unidades de medición de ángulos tienen sus ventajas.
El grado es mucho más popular. En el mundo real, es más probable que te encuentres con personas que piensan en términos de grados en lugar de radianes. Entonces, si está tratando de comunicarse con alguien que no es matemático, tal vez se limite a los grados.
Sin embargo, en cálculo, los radianes son excelentes porque se prestan a ecuaciones mucho más simples . Los futuros estudiantes de AP querrán tener eso en cuenta.
Conversión de grados a radianes (y viceversa)
Para convertir grados en radianes, solo necesita memorizar unos sencillos pasos.
Primero, tome la cantidad de grados que desea convertir. Multiplique este número por π radianes/180 grados . Al eliminar algunas unidades redundantes y luego simplificar un poco las cosas, tendrá su respuesta.
Suponga que tiene una barra de metal que se ha doblado en un ángulo de 120 grados. ¿Cómo podemos expresar esto en términos de radianes?
Para averiguarlo, escribiremos nuestra ecuación así:
120 ° x (π radianes/180 ° )
Observe el par de símbolos de grados que se muestran arriba. Esos se cancelarán entre sí, asegurando que nuestra respuesta final sea en radianes. Ahora nos quedamos con:
120 x (π radianes/180)
Haz la multiplicación y obtienes 120π/180 radianes . Pero aún no hemos terminado. Ahora tenemos que simplificar nuestra fracción si es posible. Necesitamos identificar el número entero más alto que se puede dividir exactamente tanto en el denominador (180) como en la parte que no es π del numerador (120). Alerta de spoiler: en nuestro caso, el número mágico es 60.
Si realmente divides 120π y 180 entre 60, obtienes 2π/3 radianes.
Entonces, allá vamos: 120° es igual a 2π/3 radianes.
Pasar de radianes a grados es un procedimiento similar . Solo que en este caso, tomaríamos la cantidad inicial de radianes y la multiplicaríamos por (180 ° / π ).
π/3 radianes x (180 ° / π) = 60 grados
Para resumir:
Para convertir de radianes a grados : multiplicar por 180, dividir por π
Para convertir de grados a radianes : multiplicar por π, dividir por 180
Ahora eso es interesante
La forma de "anillo", formada por dos círculos concéntricos que comparten el mismo centro, se denomina técnicamente " anillo ".















































