Фермионная физика

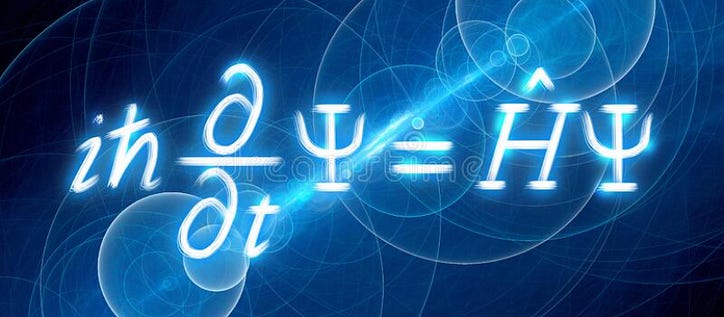
Если вы изучали квантовую физику или хотя бы слышали о ней, возможно, вы слышали об этом парне Шрёдингере. Знаешь — тот, что со всем кошачьим? Что ж, он также является автором одного из самых полезных уравнений квантовой механики — уравнения Шредингера. На первый взгляд уравнение может показаться неразрешимым (а в некоторых случаях это действительно так!), но прочитав это, вы поймете уравнение и даже то, как его решить для одного сценария. Готовый? Пошли.

Вот уравнение. Кажется страшным — в нем даже есть вилы! Но давайте попробуем получить некоторое представление об этом уравнении. Сначала мы начнем с разговора об энергии в квантовой механике, переводим ее в операторы, а затем поговорим о роли волновой функции. После этого мы сошьем все вместе и решим уравнение.

Классическая механика

В классической механике (и квантовой механике) формула для энергии такова: E = KE + PE, где E — полная энергия, KE — кинетическая энергия, а PE — потенциальная энергия. Теперь для записи KE и PE требуется немного больше времени, поэтому, чтобы сэкономить несколько миллисекунд записи, физики используют очевидные символы T и V для представления кинетической и потенциальной энергии соответственно. Итак, теперь у нас есть E = T + V

Сноска: если вы изучали классическую механику, то могли заметить, что мы используем формулировку Гамильтона! Мы займемся лагранжевой формулировкой в ​​другой раз.

Теперь мы знаем, что T=p²/2m (формула кинетической энергии). Здесь m=масса, p=импульс и самый сложный символ из всех, ½=половина. Масса всегда постоянна, но импульс не обязательно. Если кто-то приложит силу к объекту, импульс начнет меняться и отклоняться от своего первоначального значения. А как насчет потенциальной энергии?

Формула потенциальной энергии: V = -(интеграл от F), где F — сила. Становится очевидным, что потенциальная энергия зависит от силы, приложенной к объекту. В разных сценариях ваша потенциальная энергия может принимать разные значения, поскольку действуют разные силы. Например, в гравитационном колодце потенциал V=mgx, а в гармоническом осцилляторе потенциал становится V=(1/2)kx². Это очень важно, потому что оказывается, что наши «сценарии», в которых мы решаем уравнение Шредингера, на самом деле просто разные потенциалы. Это будет иметь смысл позже.

Первое квантование

Теперь в квантовой механике мы берем наши «наблюдаемые» (T и E) и заставляем их иметь оператораналоги. Для наших целей оператор — это просто функция, которая принимает одно значение и выдает другое. Таким образом, T имеет аналог оператора кинетической энергии, обычно обозначаемый буквой T', а энергия принимает аналог оператора энергии, обычно обозначаемый буквой H. Потенциальная энергия «задается», а не вычисляется, поэтому она не имеет никакого значения. аналог оператора. Теперь оператор кинетической энергии определяется как оператор, в котором при воздействии на волновую функцию он возвращает кинетическую энергию частицы, умноженную на волновую функцию. То же самое с оператором Energy. Все это может показаться немного бесполезным и абстрактным, но поверьте мне, это не так — мы приближаемся к этому. Теперь помните, как T=(1/2m)p²? Отсюда следует, что T' = (1/2m)p̂², где p̂ — оператор импульса . И, как и прежде, p̂ ψ = p ψгде p — импульс частицы (опять же, оператор действует на функцию и возвращает функцию, умноженную на любое значение, связанное с оператором). Теперь оказывается, что оператор импульса равен

p̂ = -ih(d/dx). Примите это как данность пока. Это означает, что

T' = -h²/2м (d²/dx²). А так как E = T + V, то H=(-h²/2m)(d²/dx²) + V. Теперь мы можем умножить обе части на волновую функцию, чтобы получить

H ψ = -h²/2 м (d²ψ/dx²) + Vψ

И помните ранее, H ψ = Eψ, так что

E ψ = (-h²/2 м)(d²ψ/dx²) + Vψ

Теперь сделайте глубокий вдох. Мы много посчитали, и, надеюсь, вы не заблудились. Оказывается, мы только что «вывели» уравнение Шредингера! Теперь, прежде чем мы поговорим о ее решении, нам нужно поговорить о том, что вообще представляет собой эта «волновая функция».

Что такое волновая функция?

В классической механике мы используем классическое гамильтоново уравнение для решения уравнений движения частицы. Уравнения движения — это просто уравнения того, где находится частица в данный момент времени. Например, уравнение движения свободной частицы имеет вид x(t)=vt + x0. Мы можем найти положение частицы в любой момент времени, если у нас есть начальное положение и скорость. Вместо этого в квантовой механике мы используем уравнение Шредингера, чтобы найти то, что называется «волновой функцией». Сама по себе волновая функция не имеет физического смысла — она ничего не значит и ничего вам не говорит (напрямую). Что имеет смысл, так это квадрат волновой функции, который дает вам плотность вероятности. Плотность вероятности — это просто функция, которая говорит вам о шансе найти частицу в некотором диапазоне при ее измерении. Таким образом, мы можем сказать, что волновая функция — это просто «квадратный корень» из плотности вероятности. Теперь у нас наконец есть все базовые знания, чтобы говорить о том, что такое уравнение Шредингера .

Как видно из приведенного выше уравнения, все постоянно, кроме потенциальной энергии V(x). Мы берем конкретную потенциальную энергию и решаем уравнение для случая, когда у вас есть эта конкретная потенциальная энергия. Это так красиво, потому что не имеет значения, какие нагрузки есть на вашу систему, или тепло, заряд, напряжение, что угодно — вам не нужно ничего учитывать . Все, что вам нужно знать, это просто функция потенциальной энергии, и вы можете решить уравнение

(Если мы хотим быть здесь педантичными, мы могли бы сказать, что «технически» мы включаем все эти вещи в сам потенциал. Кроме того, перевернутый треугольник — это сокращение от второй производной)

Расчет

(если вам не нравится исчисление, вы можете пропустить эту часть)

Теперь давайте решим уравнение Шредингера для простого потенциала, где V(x)=0 везде. Это известно как свободная частица, поскольку результирующие силы на ней равны нулю. Он свободен от всякого угнетения! В классическом случае уравнение движения было бы x(t)=vt + x0, которое образует прямую линию на пространственно-временном графике. Давайте посмотрим, как выглядит волновая функция для квантового случая.

Поскольку V(x)=0, уравнение Шредингера принимает вид

-h²/2м(d² ψ/dx²) = Eψ

Затем мы можем сделать некоторую перестановку и получить

d² ψ/dx² = -2 мEψ/ч²

Теперь мы можем видеть, что все члены в правой части постоянны, кроме ψ. Это хорошо, потому что упрощает решение уравнения. Затем мы можем определить константу k как sqrt(2mE/h), что означает, что теперь у нас есть

d²ψ / dx² = -k²ψ

Затем мы добавляем обе части уравнения к правому члену

d²ψ/dx² + k²ψ = 0

Затем предположим, что ψ(x) = exp(rx)

и отсюда получаем

r=-k², r= +ik или -ik

Это означает, что ψ( x)=exp(ikx) или

ψ( х)=ехр(-ikx)

Поскольку уравнение линейное, мы можем взять суперпозицию (линейную комбинацию) обеих частей, чтобы получить общее решение

ψ(x) = Aexp(ikx) + Bexp(-ikx)

и мы технически сделали. Вам может быть интересно, как мы можем даже определить константы A и B. Обычно мы делаем это с помощью чего-то, что называется нормализацией, но это история в другой раз. Получается, что для этого сценария нельзя нормировать. Это причудливый язык для волновой функции, которая не стремится к нулю, когда вы уходите в бесконечность или минус бесконечность. Так для чего же значения А и В соответствуют этому состоянию? Что ж, оказывается, это на самом деле невозможное состояние, поскольку вы не можете его нормализовать. Ой!

Не волнуйтесь! Оказывается, суперпозиция всех возможных волновых функций может дать реальное состояние. Это приносит много интересных вещей само по себе, но это тоже история для следующего раза.

Спасибо за прочтение! Этот веб-сайт ужасно справляется с форматированием математических символов, поэтому часть математического текста отображается не очень хорошо. Если вы хотите увидеть видео, в котором показано то же самое, я сделал видео здесь, на моем канале Fermion Physics, о решении (хотя я говорю довольно быстро). Переключение между видео и этой статьей поможет сделать решение более понятным. До следующего раза!