
NBA 코치이자 전 선수인 제이슨 키드(Jason Kidd)가 남긴 유명한 말이 있습니다. "우리는 이 팀을 360도 뒤집을 것입니다 ! "
이런. 수학 선생님들은 그 말에 눈을 떴을 것입니다.
이미 알고 계시겠지만 원 은 정확히 360도로 이루어져 있습니다. Kidd가 약속을 지켰다면 그의 팀은 괜찮게 돌아섰을 것입니다. 문제는 분대 가 "완전히 원을 그리며" 시작 위치로 돌아올 때까지 회전을 멈추지 않는다는 것 입니다.
개선을 위한 레시피가 아닙니다. Kidd가 찾고 있던 것은 그의 팀을 180도 바꿔서 우승자로 만드는 것이었습니다!
학위, 정의
이 컨텍스트에서 각도는 각도를 측정하는 데 사용할 수 있는 단위 입니다 . 종이에서 도는 다음과 같은 도 기호로 표시됩니다. °
따라서 " 18도 "라고 쓰는 대신 간단히 " 18 ° " 라고 쓸 수 있습니다.
삼각법과 기하학에서 가장 중요한 개념 중 하나는 직각 입니다. 이것은 두 개의 수직선이 교차하는 지점에서 형성되는 각도입니다.
또한 전체 회전의 1/4을 나타냅니다.
물리적으로 무언가를 돌리고 싶다고 가정해 봅시다. 아무것. 당신은 고정된 중심점을 선택했고 그 물체를 원을 그리며 움직이려고 합니다. 작업을 끝내고 완전한 원을 그리면 전체 회전입니다. 그러나 프로세스를 25% 도중에 중단하면 전체 회전의 1/4에 불과합니다. 당신에게 직각을 제공합니다.
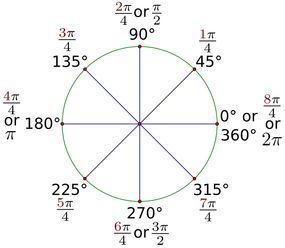
직각은 90도(즉, 360도의 25%)와 같습니다. 다른 방법이 있습니다 . 직각은 π/2 라디안 과 같습니다 .
타임아웃! 라디안은 무엇입니까? 그리고 π( pi )는 어떻게 여기에 섞였습니까?
라디안 풀기
자, 완벽한 원을 상상해 보세요. 정확한 중심에서 시작하여 원의 곡선 둘레(외부 가장자리에서와 같이)에서 끝나는 직선이 있습니다.
정의에 따르면, 그 선은 우리 원 의 반지름 입니다.
기본적으로 라디안은 원의 조각입니다. 원의 곡선 외부 둘레를 한 번 더 보십시오. 이제 길이가 원의 반지름과 같은 둘레의 한 부분을 상상해보십시오. 두 끝점을 원의 정확한 중심에 연결하는 두 개의 직선을 그린 경우 생성되는 각도는 라디안입니다.
모든 원에는 같은 수의 라디안을 위한 공간이 있습니다. 그 숫자 는 파이("π")의 2배와 같습니다. 파이 자체는 약 3.14와 같기 때문에 원(2 x 3.14)에 약 6.28 라디안이 있다고 말할 수 있습니다. 또는 1 라디안은 약 57.29도(180°/π)입니다.
라디안 대 학위
이봐, 우리는 그것을 부정하지 않을거야. 라디안은 도보다 시각화하기 어려운 개념일 수 있습니다.
그러나 전자를 할인하지 마십시오. 이러한 각도 측정 장치는 모두 장점이 있습니다.
학위가 훨씬 더 유명합니다. 현실 세계에서 라디안이 아닌 각도로 생각하는 사람들을 만날 가능성이 더 큽니다. 따라서 수학자가 아닌 사람과 의사 소통을 시도하는 경우 학위를 고수하십시오.
그러나 미적분학에서 라디안은 훨씬 더 간단한 방정식 에 적합하기 때문에 훌륭 합니다. 미래의 AP 학생들은 그것을 염두에 두고 싶어할 것입니다.
도를 라디안으로 변환(또는 그 반대로)
도를 라디안으로 변환하려면 몇 가지 간단한 단계만 기억하면 됩니다.
먼저 변환하려는 도수를 가져옵니다. 이 숫자에 π 라디안/180도를 곱합니다 . 일부 중복 단위를 제거한 다음 작업을 약간 단순화하면 답을 얻을 수 있습니다.
120도 각도로 구부러진 금속 막대가 있다고 가정합니다. 이것을 라디안으로 어떻게 표현할 수 있습니까?
알아보기 위해 방정식을 다음과 같이 작성합니다.
120 ° x(π 라디안/180 ° )
위에 표시된 도 기호 쌍을 확인하십시오. 그것들은 서로 상쇄되어 최종 답이 라디안이 되도록 합니다. 이제 다음이 남았습니다.
120 x (π 라디안/180)
곱셈을 하면 120π/180 라디안 이 됩니다. 하지만 아직 끝나지 않았습니다. 이제 가능하면 분수를 단순화해야 합니다. 분모(180)와 분자(120)의 π가 아닌 부분으로 정확히 나눌 수 있는 가장 큰 정수를 식별해야 합니다. 스포일러 경고: 우리의 경우 매직 넘버는 60입니다.
실제로 120π와 180을 60으로 나누면 2π/3 라디안이 됩니다.
120°는 2π/3 라디안과 같습니다.
라디안에서 각도로 가는 것도 유사한 절차 입니다. 이 경우에만 라디안의 시작 양을 취하고 여기에 (180 ° / π )를 곱합니다.
π/3 라디안 x (180 ° / π) = 60도
요약:
라디안에서 도로 변환하려면 180을 곱하고 π로 나눕니다.
도에서 라디안으로 변환하려면 π를 곱하고 180으로 나눕니다.
흥미롭네요
동일한 중심을 공유하는 두 개의 동심원으로 구성된 "고리" 모양을 기술적으로 " 환형 "이라고 합니다 .















































