İstatistik - Beta Dağılımı

Beta dağılımı, rastgele x değişkeninin üsleri olarak görünen ve dağılımın şeklini kontrol eden iki pozitif şekil parametresi, $ \ alpha $ ve $ \ beta $ ile parametrelendirilen sürekli olasılık dağılımını temsil eder.

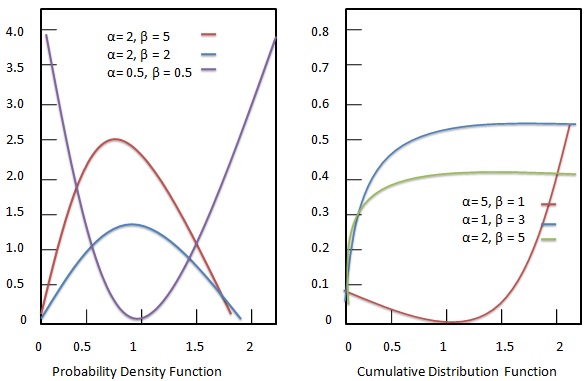
Olasılık yoğunluk işlevi

Beta dağılımının olasılık yoğunluğu işlevi şu şekilde verilir:

Formül

$ {f (x) = \ frac {(xa) ^ {\ alpha-1} (bx) ^ {\ beta-1}} {B (\ alpha, \ beta) (ba) ^ {\ alpha + \ beta- 1}} \ hspace {.3in} a \ le x \ le b; \ alpha, \ beta> 0 \\ [7pt] \, burada \ B (\ alpha, \ beta) = \ int_ {0} ^ {1} {t ^ {\ alpha-1} (1-t) ^ { \ beta-1} dt}} $

Nerede -

$ {\ alpha, \ beta} $ = şekil parametreleri.
$ {a, b} $ = üst ve alt sınırlar.
$ {B (\ alpha, \ beta)} $ = Beta işlevi.

Standart Beta Dağıtımı

Üst ve alt sınırların 1 ve 0 olması durumunda beta dağılımına standart beta dağılımı denir. Aşağıdaki formülle yürütülür:

Formül

$ {f (x) = \ frac {x ^ {\ alpha-1} (1-x) ^ {\ beta-1}} {B (\ alpha, \ beta)} \ hspace {.3in} \ le x \ le 1; \ alpha, \ beta> 0} $

Kümülatif dağılım fonksiyonu

Beta dağılımının kümülatif dağılım işlevi şu şekilde verilmiştir:

Formül

$ {F (x) = I_ {x} (\ alpha, \ beta) = \ frac {\ int_ {0} ^ {x} {t ^ {\ alpha-1} (1-t) ^ {\ beta- 1} dt}} {B (\ alpha, \ beta)} \ hspace {.2in} 0 \ le x \ le 1; p, \ beta> 0} $

Nerede -

$ {\ alpha, \ beta} $ = şekil parametreleri.
$ {a, b} $ = üst ve alt sınırlar.
$ {B (\ alpha, \ beta)} $ = Beta işlevi.

Eksik beta fonksiyon oranı olarak da adlandırılır.