İstatistik - İkinci Dereceden Regresyon Denklemi

İkinci dereceden regresyon, verilen veri setine en iyi uyan parabol denklemini bulmak için kullanılır. Aşağıdaki biçimdedir:

$ {y = ax ^ 2 + bx + c \ burada \ a \ ne 0} $

Karesel Regresyon Denklemini bulmak için en küçük kareler yöntemi kullanılabilir. Bu yöntemde, verilen her nokta ($ {x_i, y_i} $) ile parabol denklemi ($ {y = ax ^ 2 + bx + 2} arasındaki dikey mesafenin karesi alınacak şekilde a, b ve c'nin değerini buluruz. $) minimumdur. Parabolik eğri için matris denklemi şu şekilde verilir:

$ {\ begin {bmatrix} \ sum {x_i} ^ 4 & \ sum {x_i} ^ 3 & \ sum {x_i} ^ 2 \\ \ sum {x_i} ^ 3 & \ sum {x_i} ^ 2 & \ sum x_i \\ \ sum {x_i} ^ 2 & \ sum x_i & n \ end {bmatrix} \ begin {bmatrix} a \\ b \\ c \ end {bmatrix} = \ begin {bmatrix} \ sum {x_i} ^ 2 {y_i} \\ \ sum x_iy_i \\ \ sum y_i \ end {bmatrix}} $

Korelasyon Katsayısı, r

Korelasyon katsayısı, r, bir kuardratik denklemin verilen verilere ne kadar iyi uyabileceğini belirler. R, 1'e yakınsa, o zaman iyi uyumdur. r aşağıdaki formülle hesaplanabilir.

$ {r = 1 - \ frac {SSE} {SST} \ burada \\ [7pt] \ SSE = \ sum (y_i - a {x_i} ^ 2 - bx + i - c) ^ 2 \\ [7pt] \ SST = \ toplam (y_i - \ bar y) ^ 2} $

Genel olarak, ikinci dereceden regresyon hesaplayıcıları ikinci dereceden regresyon denklemini hesaplamak için kullanılır.

Misal

Problem Statement:

Aşağıdaki verilerin ikinci dereceden regresyon denklemini hesaplayın. En iyi formunu kontrol edin.

x	-3	-2	-1	0	1	2	3
y	7.5	3	0.5	1	3	6	14

Solution:

Hesap makinesinde x ve y değerlerini koyarak ikinci dereceden bir regresyon hesaplayın. Yukarıdaki noktalar için en uygun ikinci dereceden denklem şu şekilde gelir:

$ {y = 1,1071x ^ 2 + 0,5714x} $

En iyi zindeliği kontrol etmek için grafiği çizin.

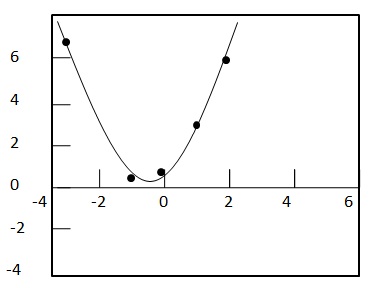
Dolayısıyla, veriler için Korelasyon Katsayısı r değeri 0.99420'dir ve 1'e yakındır. Bu nedenle ikinci dereceden regresyon denklemi en uygunudur.