İstatistik - Ki-kare Dağılımı

Serbestlik dereceli ki-kare dağılımı (ki-kare veya $ {X ^ 2} $ - dağılımı), k, k bağımsız standart normal rasgele değişkenlerin karelerinin toplamının dağılımıdır. İstatistikte en yaygın kullanılan olasılık dağılımlarından biridir. Bu, gama dağılımının özel bir durumudur.

Ki-kare dağılımı, istatistikçiler tarafından aşağıdakileri hesaplamak için yaygın olarak kullanılır:

Örnek bir standart sapma kullanılarak normal dağılımın popülasyon standart sapması için Güven aralığı tahmini.
Çoklu nitel değişkenlerin iki sınıflandırma kriterinin bağımsızlığını kontrol etmek.
Kategorik değişkenler arasındaki ilişkileri kontrol etmek.
Altta yatan dağılımın normal olduğu örnek varyansı incelemek.
Beklenen ve gözlemlenen frekanslar arasındaki farklılıkların sapmalarını test etmek.
Ki-kare testi yapmak (bir uyum iyiliği testi).

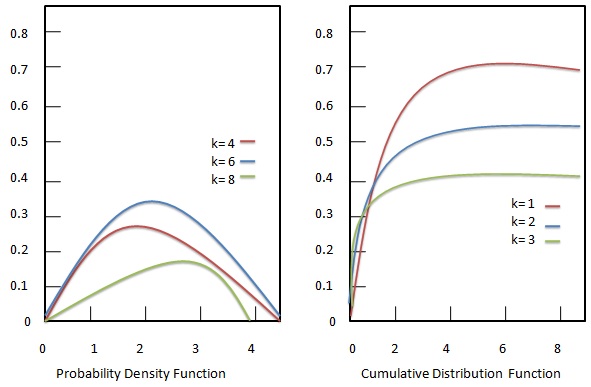
Olasılık yoğunluk işlevi

Ki-Kare dağılımının olasılık yoğunluk fonksiyonu şu şekilde verilir:

Formül

$ {f (x; k) =} $ $ \ başlar {case} \ frac {x ^ {\ frac {k} {2} - 1} e ^ {- \ frac {x} {2}}} {2 ^ {\ frac {k} {2}} \ Gama (\ frac {k} {2})}, & \ text {if $ x \ gt 0 $} \\ [7pt] 0, & \ text {if $ x \ le 0 $} \ end {case} $

Nerede -

$ {\ Gamma (\ frac {k} {2})} $ = k tamsayı parametresi için kapalı form değerlerine sahip gama işlevi.
$ {x} $ = rastgele değişken.
$ {k} $ = tamsayı parametresi.