İstatistikler - Grafikleri karşılaştırma
Nüfus grupları, kutu ve bıyık grafikleri kullanılarak karşılaştırılabilir. Medyan arasındaki genel görünür yayılma ve fark, iki grup arasında bir fark olup olmadığı sonucuna varmak için kullanılır.
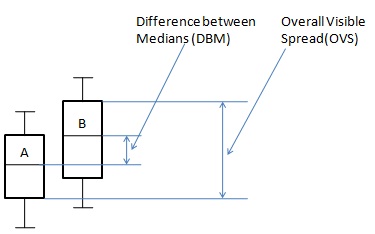
Durum 2: Formül
$ {P = \ frac {DBM} {OVS} \ times 100} $
Nerede -
$ {P} $ = yüzde farkı
$ {DBM} $ = Medyanlar Arasındaki Fark.
$ {OVS} $ = Genel Görünür Fark.
Kurallar
30'luk bir örneklem büyüklüğü için, bu yüzde% 33'ten büyükse, iki grup arasında bir fark olma eğilimindedir.
100 örneklem büyüklüğü için, bu yüzde% 20'den büyükse, iki grup arasında bir fark olma eğilimindedir.
1000'lik bir örneklem büyüklüğü için, bu yüzde% 10'dan büyükse, iki grup arasında bir fark olma eğilimindedir.
Misal
Sorun bildirimi:
Aşağıdaki veri kümeleri arasındaki farkı tanımlayın.
| Sr. No. | İsim | A ayarla | B ayarla |
|---|---|---|---|
| 1 | Max | 12 | 15 |
| 2 | UQ | 10 | 13 |
| 3 | Medyan | 7 | 10 |
| 4 | LQ | 6 | 9 |
| 5 | Min | 5 | 6 |
Çözüm:
Aşağıdaki şemayı düşünün:
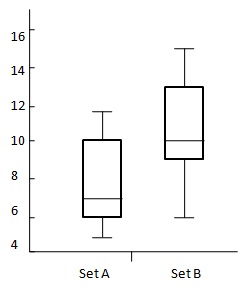
$ {OVS = 13 - 6 \\ [7pt] \ = 7 \\ [7pt] \ DBM = 10-3 \\ [7pt] \ = 4} $
Formülü uygulayın
$ {P = \ frac {DBM} {OVS} \ times 100 \\ [7pt] \ = \ frac {4} {7} \ times 100 \\ [7pt] \ = 57.14} $
Yüzde,% 33'ün üzerinde olduğundan, bu nedenle Set A ve Set B arasında fark vardır. Set B muhtemelen Set A'dan daha büyüktür.